Право. Теплофизика Вар 1. Теплофизика вариант 1 Вопрос Какими основными параметрами характеризуется состояние рабочего тела Приведите уравнения состояния идеального газа для 1 кг, m кг, 1 кмоль газа
 Скачать 354.18 Kb. Скачать 354.18 Kb.
|
|
ТЕПЛОФИЗИКА Вариант № 1 Вопрос № 2. Какими основными параметрами характеризуется состояние рабочего тела? Приведите уравнения состояния идеального газа для 1 кг, m кг, 1 кмоль газа. Для определения конкретных физических условий, в которых находится термодинамическая система, используют ряд показателей, называемых параметрами состояния. В число основных параметров входят: абсолютная температура, абсолютное давление и удельный объем. Абсолютная температура – это мера кинетической энергии движения молекул. Она характеризует тепловое состояние тела. Температуру измеряют по абсолютной шкале в градусах Кельвина (К) и обозначают буквой Т, либо по Международной практической системе единиц в градусах Цельсия (°С) и обозначают t. В качестве реперной точки этих двух температур взята тройная точка чистой воды, при которой все три фазы воды (лед, вода и пар) находятся в равновесии друг с другом. Температура в такой точке соответствует значениям 273,15 К и 0,01°С. Таким образом, связь между единицами измерения температуры в Кельвинах и Цельсиях можно выразить: Абсолютное давление – это средняя сила, с которой молекулы вещества действуют на единицу площади сосуда. Обозначают абсолютное давление буквой р. Измеряют давление в ньютонах деленных на квадратный метр Н/м2 или в паскалях Па (1Н/м2 =1Па). Так как эти единицы измерения для практических целей очень малы, то давление может измеряться в барах (1бар = 105Па). В технической системе (МКГСС) за единицу силы принимают килограмм-силу (кгс), тогда единица измерения давления может быть выражена кгс/м2 (1кгс/м2 = 9,8 Па). Эта единица измерения также мала, поэтому в технической системе за единицу измерения давления принимают техническую атмосферу ат тех. (1 ат тех. = 104 кгс/м2 = 1кгс/см2 = 0,98 бар). Давление также измеряю высотой столба жидкости. Например: 1 ат тех = 735 мм рт. ст. = 10 м вод. ст. (при 0°С). Следует сказать, что под действием давления и температуры столб жидкости может менять свой объем, поэтому давление рабочего тела жидкостным столбом измеряют при нормальных физических условиях (760 мм рт. ст. и 0 °С). В этом случае атмосферу называют физической. 1 ат физ. = 1,033 ат тех. = 760 мм рт. ст. = 101,3 кПа = 10,33 м вод. ст. Под абсолютным давлением понимают действительное давление рабочего тела внутри сосуда. Давление жидкостей, паров или газов обычно измеряют приборами барометрического типа, приборами манометрического типа и вакуумметрами. Барометры измеряют давление окружающей среды В. Манометры меряют разность между абсолютным давлением в сосуде и давлением в окружающей среды, то есть избыточное давление ри. Следовательно, когда давление в сосуде превышает давление среды, абсолютное давление рабочего тела будет определяться: Вакуумметры показывают разность давления окружающей среды и абсолютного давления в сосуде, то есть разряжение или вакуум рв. В этом случае абсолютное давление можно найти: Удельный объем – это объем, занимаемый рабочим телом массой 1 кг. Удельный объем обозначают буквой v и измеряют в кубических метрах, деленных на килограмм (м3/кг). Если V это объем тела, м3, занимаемый массой М, кг, то Обратной величиной удельному объему является плотность ρ (кг/м3): v = 1/ρ или v∙ρ =1. В каждом конкретном случае все параметры состояния рабочего тела однозначно связаны друг с другом. Зная эту зависимость и задавшись какими-либо двумя параметрами, можно найти остальные неизвестные параметры. Метод их определения зависит от того, в каком виде – аналитическом, графическом или табличном – представлена эта зависимость. Аналитическая зависимость параметров состояния представляет собой уравнение состояния. Для идеального газа используется уравнение Менделеева-Клапейрона. Для 1 кг газа оно запишется: Для газа массой М кг это уравнение примет вид: Для 1 киломоля газа: 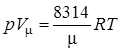 , ,где R –– газовая постоянная, независящая от состояния газа, Дж/(кг∙К); Vμ –– объем 1 киломоля газа, м3/кмоль; μ –– молярная масса газа, кмоль. Для многих реальных газов уравнение состояния имеет очень громоздкий вид и для расчетов такое уравнение трудно использовать. Поэтому параметры состояния реальных газов, а также жидкостей определяют табличным или графическим способом. В таблицах заносят массив значений параметров состояния вещества, из которого выбираются искомые значения при заданных двух параметрах состояния (обычно при температуре и давлении). Для графического определения параметров состояния используют p-v, T-S и i-S диаграммы. На этих диаграммах наносят семейства изобар, изохор, изотерм и адиабат. Одно из свойств таких диаграмм состоит в том, что каждому состоянию рабочего тела соответствует точка на диаграмме. Для рассчитываемого состояния она лежит на пересечении линий двух исходных параметров. При подводе одного итого же количества теплоты к различным телам они изменяют свою температуру на разную величину. Это происходит вследствие того, что тела обладают разной теплоемкостью. Теплоемкостью называют количество теплоты, которое необходимо сообщить телу, чтобы изменить его температуру на 1 градус. В зависимости от того, в каких единицах задано количество вещества теплоемкость различают: массовую с кДж/(кг∙К); объемную с/ кДж/(м3∙К); молярную сμкДж/(кмоль∙К). Связь между ними выражается следующей зависимостью: 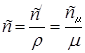 . .Если –– q количества тепла, сообщаемого единице количества газа при изменении температуры газа от Т1 до Т2 то величина 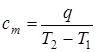 будет представлять собой среднюю теплоемкость в пределах Т1 – Т2. Тогда количество сообщенной телу теплоты будет определяться: где т –– масса газа, кг; Vн –– объем газа приведенный к нормальным физическим условиям, м3; п –– число молей газа. Вопрос № 12. Изобразите процесс парообразования в Тs- и is-диаграммах и объясните характерные линии области и точки на полученных диаграммах. Процесс идеального газа, в котором теплоемкость является постоянной называется политропным, а линия процесс - политропой. Из определения политропного процесса следует, что основные термодинамические процессы - изохорный, изобарный, изотермический и адиабатный, если они протекают при постоянной теплоемкости, являются частными случаями политропного процесса. Теплоемкость политропного процесса Количество теплоты, участвующее в политропном процессе. может быть выражено произведением теплоемкости процесса Уравнение политропного процесса выводится на основании уравнения первого закона термодинамики: Из этих уравнений найдем 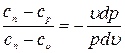 Обозначив выражение левой части уравнения через 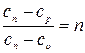 и и 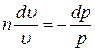 Интегрируя полученное соотношение в пределах от начала до конца процесса, находим 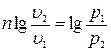 или Полученное уравнение является уравнением политропного процесса. Показатель политропы Фазовая Пусть вода, масса которой 1 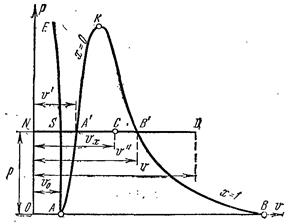 Рисунок 1 Вся кривая График зависимости Если процесс парообразования протекает при постоянном давлении, то температура его не изменяется и процесс График зависимости удельного объема Точка Если к сухому насыщенному пару подводить теплоту при постоянном давлении, то температура и объем его будут увеличиваться и пар из сухого насыщенного перейдет в перегретый (точка Обе кривые Критическая точка является конечной точкой фазового перехода жидкость - пар, начинающейся в тройной точке. Выше критической точки существование вещества в двухфазном состоянии невозможно. Никаким давлением нельзя перевести газ в жидкое состояние при температурах выше критической. Область, заключенная между изотермой воды при температуре Графически на 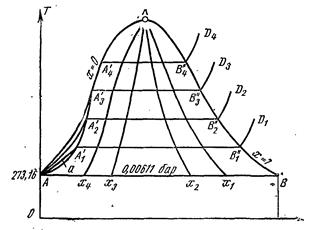 Рисунок 2 Если нанести на диаграмме ряд таких изобарных процессов и соединить характерные точки, то получим пограничные кривые кипящей жидкости Пограничная кривая жидкости выходит из оси ординат при температуре Пограничные кривые делят диаграмму на 3 части: влево от На диаграмму наносят изобары, линии постоянных удельных объемов, а в области влажного пара - линии равных степеней сухости, в этой области влажного пара - линии равных степеней сухости, в этой области изобары представляют собой прямые линии, параллельные оси абсцисс, а в области перегретого пара - кривые линии На Вопрос № 30. Что называется теплопередачей? Приведите уравнение теплопередачи для плоской стенки. Объясните физический смысл коэффициента теплопередачи. Теплопередача - физический процесс передачи тепловой энергии от более горячего тела к более холодному либо непосредственно (при контакте), либо через разделяющую (тела или среды) перегородку из какого-либо материала. Когда физические тела одной системы находятся при разной температуре, то происходит передача тепловой энергии, или теплопередача от одного тела к другому до наступления термодинамического равновесия. Самопроизвольная передача тепла всегда происходит от более горячего тела к более холодному, что является следствием второго закона термодинамики Виды теплообмена Всего существует три простых (элементарных) вида передачи тепла: • Теплопроводность • Конвекция • Тепловое излучение Существуют также различные виды сложного переноса тепла, которые являются сочетанием элементарных видов. Основные из них: • теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела); • теплопередача (теплообмен от горячей жидкости к холодной через разделяющую их стенку); • конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией); • термомагнитная конвекция Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена. При передаче теплоты от стенки к окружающей среде в основном преобладает конвективный теплообмен, поэтому будут рассматриваться такие задачи. 1). Теплопередача через плоскую стенку. Рассмотрим однослойную плоскую стенку толщиной d и теплопроводностью l (рис12.1). 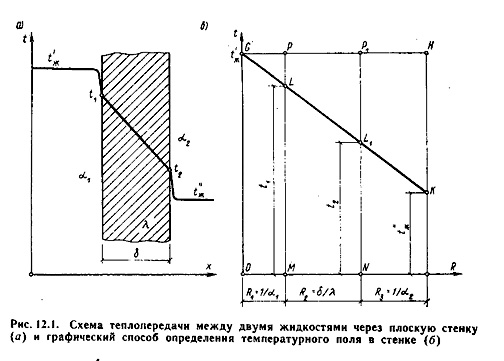 Температура горячей жидкости (среды) t'ж, холодной жидкости (среды) t''ж. Количество теплоты, переданной от горячей жидкости (среды) к стенке по закону Ньютона-Рихмана имеет вид: Q = a1 · (t'ж – t1) · F, где a1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; F – расчетная поверхность плоской стенки. Тепловой поток, переданный через стенку определяется по уравнению: Q = l/d · (t1 – t2) · F. Тепловой поток от второй поверхности стенки к холодной среде определяется по формуле: Q = б2 · (t2 - t''ж) · F где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем: Q = (t'ж – t''ж) • F • К, где К = 1 / (1/a1 + / l + 1/a2) – коэффициент теплопередачи, или R0 = 1/К = (1/a1 + d/l + 1/a2) – полное термическое сопротивление теплопередачи через однослойную плоскую стенку. 1/a1, 1/a2 – термические сопротивления теплоотдачи поверхностей стенки; d/l - термическое сопротивление стенки. Для многослойной плоской стенки полное термическое сопротивление будет определяться по следующей формуле: R0 = (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), а коэффициент теплопередачи: К = 1 / (1/a1 + d1/l1 + d2/l2 + … + dn/ln +1/a2), Коэффициент теплопередачи показывает, какое количество теплоты в Дж переходит в 1с от более нагретого тела к менее нагретому через поверхность теплообмена в 1м2 при средней разности температур равной 1 град. Коэффициент теплопередачи определяет интенсивность теплообмена. Из основного уравнения теплопередачи можно определить поверхность теплопередачи 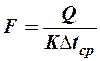 . .Задача № 1 «Расчет теоретического цикла газотурбинной установки» Для теоретического цикла ГТУ с подводом теплоты при постоянном давлении определить параметры рабочего тела (воздуха) в характерных точках цикла, подведённую и отведенную теплоту, работу и термический КПД цикла, если начальное давление р1=0,1 МПа, начальная температура t1=27 0С, степень повышения давления в компрессоре β=6,5, температура газа перед турбиной t3=725 0С. Определить также термический КПД цикла Карно, осуществляемого в том же интервале температур. Определить теоретическую мощность ГТУ при заданном расходе воздуха mτ=25 кг/с. Привести схему и цикл установки в pv- и Ts-диаграммах. Исходные данные: 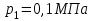 ; ; 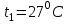 ; ; 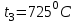 ; ;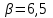 ; ; 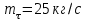 Решение: 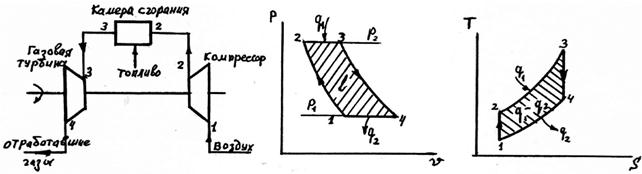 Рис.1. Схема цикла ГТУ  Рис.2. Цикл установки ГТУ в pv- и Ts-диаграммах. Определяем параметры в узловых точках цикла. Точка 1. р1 = 0,1 МПа, Т1= t1 + 273 = 27 +273 = 300К. Удельный объём определяем из уравнения состояния^ 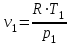 , ,где R = 287 Дж/(кг·К) – газовая постоянная для воздуха. 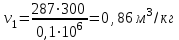 Точка 2. Определим давление через степень повышения давления: 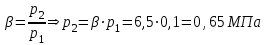 Для определения удельного объёма воспользуемся соотношением для адиабатного процесса (процесс 1-2): 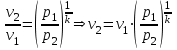 , ,k = 1,4 - показатель адиабаты для воздуха. 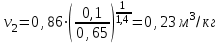 Для определения температуры воспользуемся уравнением состояния: 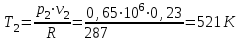 Точка 3. Так как 2 – 3 – изобара, то p3 = p2 = 0,65·106 Па. Температура Т3 = t3 + 273 = 725 + 273 = 998К. Для определения удельного объема воспользуемся уравнением состояния: 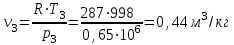 Точка 4. Так как процесс 4-1 – изобарное сжатие, то р4 = р1 = 0,1 МПа. Для определения удельного объёма воспользуемся соотношением для адиабатного процесса (процесс 3-4): 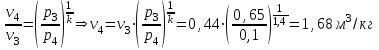 Для определения температуры воспользуемся уравнением состояния: 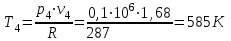 Результаты расчётов сведём в таблицу 1. Таблица 1.Параметры в характерных точках цикла.
2. Определяем подведённую теплоту. 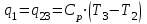 , ,где Ср=1,01 кДж/кг – изобарная теплоёмкость воздуха. 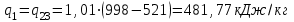 3. Определяем отведённую теплоту. 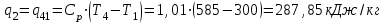 4. Определяем работу цикла. 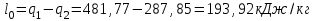 5. Термический КПД цикла: 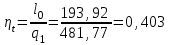 6. Термический КПД цикла через степень повышения давления: 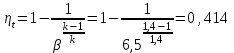 7. Термический КПД Карно: 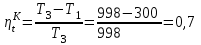 6. Теоретическая мощность ГТУ: 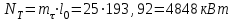 Задача № 2 «Определение поверхности нагрева рекуперативного теплообменника» Определить поверхность нагрева рекуперативного газовоздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей и массовый расход воздуха, если массовый расход продуктов сгорания mτП.С.=4,5 кг/с, средний коэффициент теплоотдачи от продуктов сгорания к омываемой ими поверхности α1=25 Вт/(м2∙К), а от поверхности к воздуху – α2=15 Вт/(м2∙К); толщина разделительной стальной стенки δ=7 мм, ее коэффициент теплопроводности λ=50 Вт/(м∙К). Начальная и конечная температуры продуктов сгорания: t1׳ = 625 0C, t1״= 4300C; начальная и конечная температуры воздуха: t2׳ = 200C, t2״ = 340 0C; тепловые потери в окружающую среду оцениваются коэффициентом ηт.а.=0,98. Привести графики изменения температур теплоносителей по длине теплообменника для прямоточной и противоточной схем движения теплоносителей. При расчете принять среднюю теплоемкость воздуха срВ=1,02кДж/(кг∙К), среднюю теплоемкость продуктов сгорания срП.С.=1,2кДж/(кг∙К). Исходные данные: 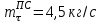 ; ; 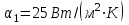 ; ; 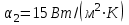 ; ;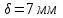 ; ; 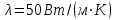 ; ; 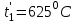 ; ; 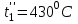 ; ;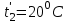 ; ; 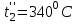 ; ; 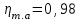 Решение: Определим количество теплоты отданное продуктами сгорания: 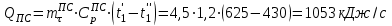 Определим массовый расход воздуха из уравнения теплового баланса: 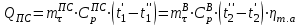 Отсюда получаем: 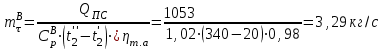 Определим коэффициент теплопередачи: 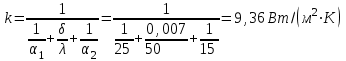 Определим температурный напор при прямоточном теплообменнике: 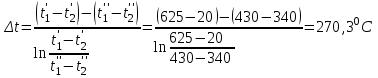 Определим необходимую площадь прямоточного теплообменника: 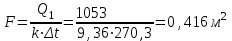 Определим температурный напор при противоточном теплообменнике: 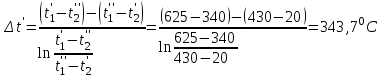 Определим необходимую площадь прямоточного теплообменника: 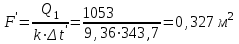 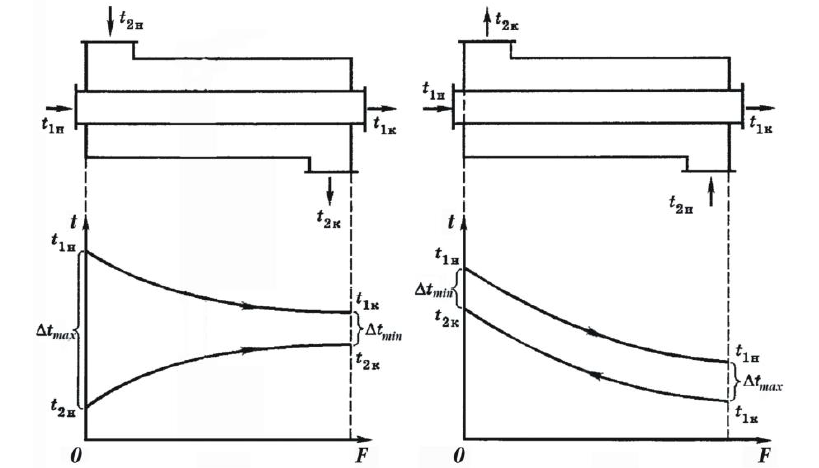 Рис.3. Графики изменения температур теплоносителей теплообменника для прямоточной и противоточной схем движения теплоносителей. |
