ПРАКТИКА ФТТ БА 2. Тепловые свойства твердых тел Теория. Основные понятия и формулы Термодинамическая система
 Скачать 402 Kb.
|
|
Тепловые свойства твердых тел 1. Теория. Основные понятия и формулы Термодинамическая система– система, состоящая из столь большого числа частиц, что ее состояние можно описывать усредненными макроскопиче- скими параметрами (такими как давление, температура, концентрация и др.). Внутренняяэнергия.Если в системе не происходит химических превращений, то внутренняя энергия – это энергия хаотического теплового дви- жения: кинетическая энергия движения молекул, потенциальная энергия их взаимодействия, кинетическая энергия движения атомов в молекулах и потенциальная энергия их взаимодействия. Температура – это мера кинетиче- ской энергии хаотического движения молекул. Первое начало термодинамики – закон изменения внутренней энергии (уравнение энергетического баланса): в закрытой системе (с постоянным числом частиц) существуют два способа изменения внутренней энергии dUсистемы – теплообмен dQ(тепловое взаимо- действие – более подробно см. стр. 5) и совершение системой работы dA (механическое взаимодействие): dU= -dA+ dQ. (1) Теплота(количество теплоты) dQ – это энергия в форме молекулярного движения, переданная без совершения работы. Элементарная механическая работа, например, сил давления при расширении против сил внешнего давления – это работа, совершаемая системой при бесконечно малом изменении объема dV: dA= pdV (2) Теплоемкостьсистемы – отношение элементарного количества теплоты dQ , которое следует подвести к системе в определенном процессе, чтобы увеличить ее температуру на бесконечно малую величину dT , к этому измене- нию температуры (измеряется теплоемкость в Дж/град): Cs= dQ. (3) dT Теплоемкость единицы массы вещества называется удельной теплоемкостью и в дальнейшем обозначается как c=dQ=1 Cs. (4) mdTm где m– масса вещества. В физике наиболее часто используется теплоемкость одного моля вещества (в дальнейшем записывается большой буквой Сбез индекса): cQ1 Cs Mc, (5) dT где n – число молей вещества, М– молярная масса. Теплоемкость зависит не только от вещества, но и от процесса, при кото- ром подводится тепло. Если в этом процессе работа не совершается, т.е. V = const, теплоемкость определяется только внутренней энергией и обычно обозначается СV. Зависимость СV оттемпературы– это уникальная характеристика каждого вещества. На основании этой зависимости можно сделать вы- воды о строении молекул, их взаимодействии и энергии взаимодействия атомов в молекулах. Удельная теплоемкость вещества  m – масса вещества, Q – количество теплоты, необходимое для изменения температуры данной массы вещества от Т1 до Т2. Молярная теплоемкость  М – молярная масса вещества. Теплоемкость твердых тел. Поскольку коэффициент теплового расшире ния твердых тел весьма мал, то можно считать, что для веществ в твердом состоянии теплоемкость при постоянном давлении Cp≈ CV. ЗаконДюлонга и Пти.Дюлонг и Пти опытным путем в 1819 году полу- чили и сформулировали правило, согласно которому молярная теплоемкость твердых тел близка к 3R– примерно 25 (Дж/мольК): С=3R, (6) где R – универсальная газовая постоянная. Как показали дальнейшие исследова- ния, этот закон дает хорошее соответствие с экспериментом для многих веществ в кри- сталлическом состоянии, но только при тем- пературах выше определенного значения – Дебаевской температуры (Т > TD), которая имеет свою величину для каждого вещества. Дюлонг и Пти проводили исследования примерно при комнатной температуре (15°C – 100 °C). Последовательная теория теплоемкости твердых тел возможна только в рамках квантовой теории (модели Эйнштейна и Дебая). Теплота кристаллизации.Кристаллизация – процесс перехода вещества из жидкого состояния в твердое. Процесс кристаллизации связан с выделением количества теплоты, равного теплоте плавления. Для химически однородных веществ и некоторых сплавов процесс кристаллизации протекает при постоянной температуре, равной температуре плавления. В процессе кристаллизации упорядочивается движение частиц жидкости, постепенно прекращается перемещение молекул, возникают связанные тепловые колебания относительно узлов кристаллической решетки. Для начала кристаллизации необходимо, чтобы в жидкости имелись центры кристаллизации – неоднородности, вокруг которых начинается процесс образования твердой фазы. Если жидкость очень чистая и центры кристаллизации отсутствуют, то она может быть охлаждена до температуры более низкой, чем температура кристаллизации, но это состояние неустойчиво. 2 Примеры решения задач Задача 4 Алюминиевый брусок нагрели на 1 градус. Какое напряжение надо приложить к бруску, чтобы при нагревании его длина осталась неизменной? Анализ и решение 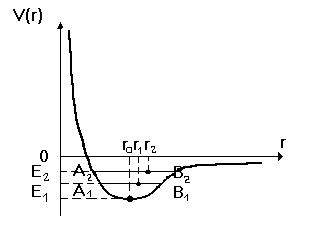 При нагревании алюминиевого бруска на 1 градус увеличивается амплитуда тепловых колебаний атомов в узлах кристаллической решетки. Однако это увеличение амплитуды одинаково для всех атомов бруска, среднее расстояние между двумя соседними атомами не изменяется, и, следовательно, увеличение амплитуды колебаний при повышении температуры само по себе не ведет к тепловому расширению. Для того, чтобы выяснить причину теплового расширения бруска обратимся к графику зависимости потенциальной энергии взаимодействия двух атомов твердого тела от расстояния между ними. Кривая потенциальной энергии асимметрична вблизи r0 (положения равновесия при О.К), т.е. её форма отличается от параболы. При температурах T1 и T2 (T2 > T1), с соответствующими полными энергиями E1 и E2, частица будет совершать тепловые колебания. Для T1 частица отклоняется влево до точки A1 и вправо до точки B1. При этом среднее положение колеблющейся частицы не совпадает с r0, а сместится вправо и примет значение r1. При более высокой темпиратуре T2 частица будет отклонятся от A2 и B2, а среднее положение примет значение r2. Таким образом, при возрастании температуры увеличиваются расстояния между узлами кристаллической решетки, т. е. происходит тепловое расширение тела. Для того, чтобы при нагревании на 1 градус длина осталась неизменной, надо к телу приложить напряжение (силу на единицу площади поперечного сечения) и вернуть атомы твердого тела в первоначальные положения равновесия, которые соответствовали температуре на 1 градус меньше. Для количественной оценки вспомним, что при нагревании твердого тела на температуру  T его удлинение пропорционально первоначальной длине l0 и изменению температуры:l = l0 T , где  -коэффициент линейного расширения для алюминия =2,610-5 грaд-1.Таким образом, при нагревании алюминиевого бруска на T=1 градус относительное удлинение :l/ l0 = T = 2,610-5 , т. е. равновесное состояние между атомами увеличилось в среднем на 2,б10-5 от первоначального расстояния. По закону Гука относительное сжатие на эту величину определит искомое напряжение  :l/ l0 = / E , где E – модуль Юнга. Откуда T = / E , = ET Модуль Юнга для алюминия E = 6,91010 н/м2. Таким образом, = 1,8106 н/м2 = 1,810 6 Па. Задача 5 Определите квазиимпульс p , фонона, соответствующего частоте =0,1 д , где д - характеристическая частота Дебая. Средняя скорость V звука в кристалле равна 1380 м/с, температура Дебая  = 100 К. Дисперсией звуковых волн в кристалле пренебречь.Решение Для фонона с волновым вектором |
квазиимпульс определяется как:
,
-частота фонона, 
-ср. скорость звука.
и 
, т. е. 
, где k- постоянная Больцмана.
.
, находим 
.
.
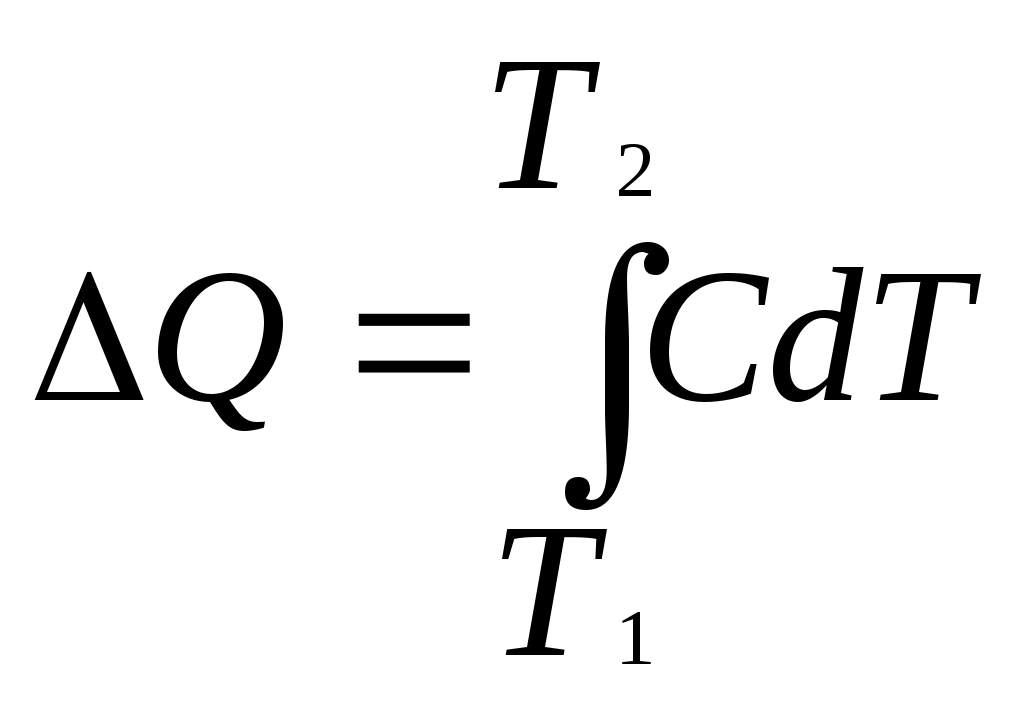, где С – теплоемкость тела.
, связанная с теплоекостью всего тела соотношением:
; где m – масса тела , -молярная масса, = 58,4 г/моль.
.
.
, 
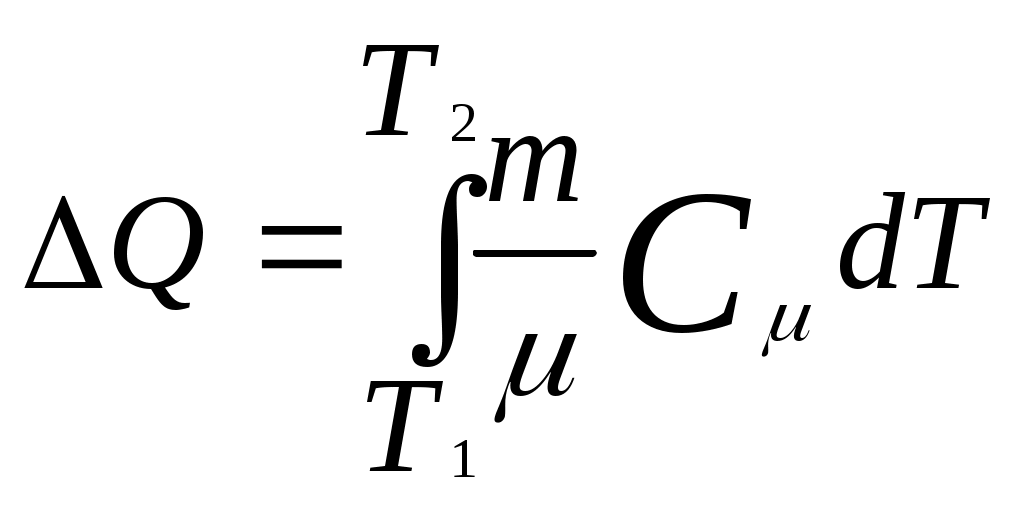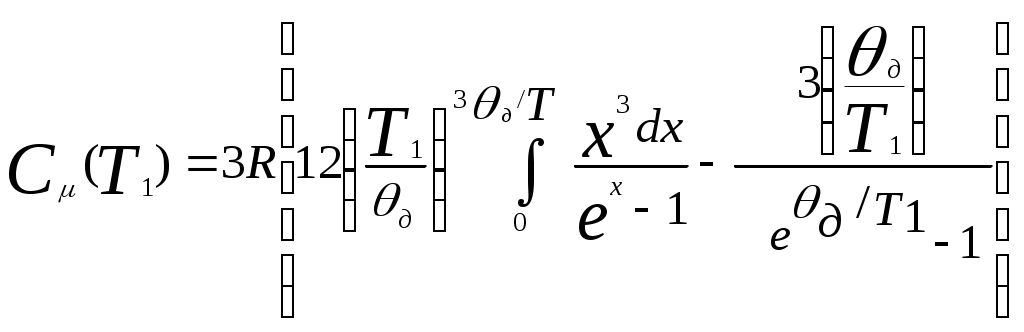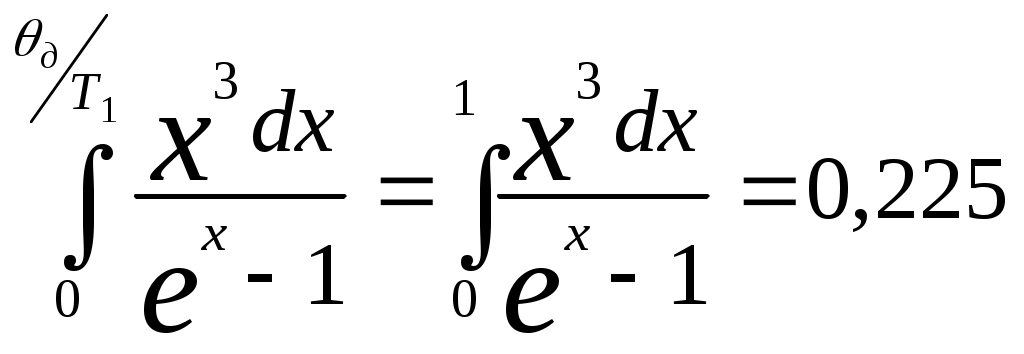(см. Двайт Г.Б. Таблицы интегралов и другие математические формулы – М.Наука, 1977).
.
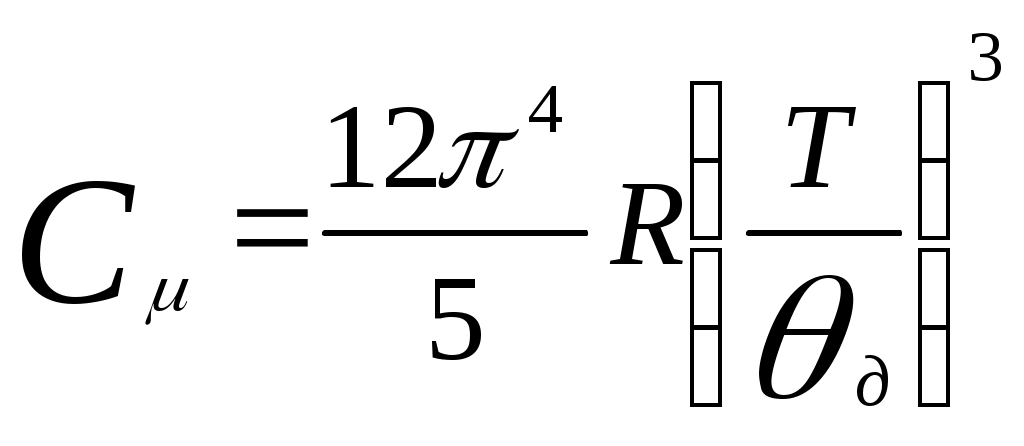, тогда получаем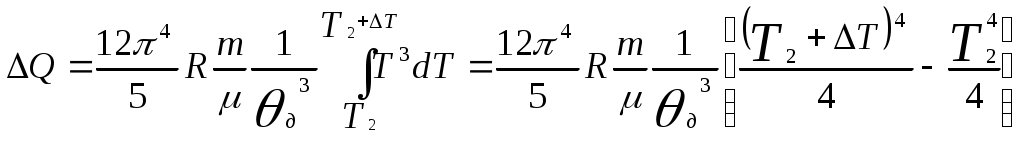 
.
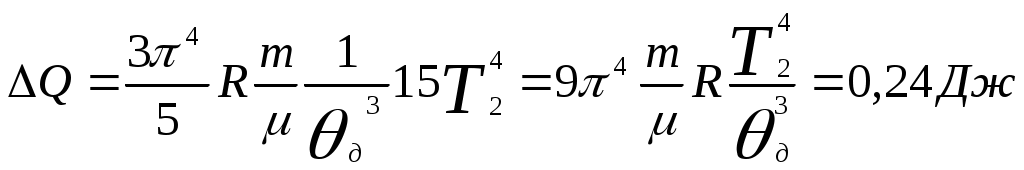