Прикл.механ. реш.задач. Руководство к решению контрольных задач по дисциплине и примеры решения задач Москва мгоу 2009 год аннотация
 Скачать 0.78 Mb.
|
|
Министерство образования и науки Российской Федерации Московский государственный открытый университет Серия открытое образование Прикладная механика Руководство к решению контрольных задач по дисциплине и примеры решения задач Москва МГОУ 2009 год АННОТАЦИЯ В пособии представлены примеры решения контрольных задач, которые выполняют студенты при изучении дисциплины «Прикладная механика ». Представленные примеры помогают студентам понять ход решения задачи и сравнивать величины приведенных в пособии и получаемых результатов расчетов. В ходе выполнения решений задач необходимо пользоваться таблицами и графиками из учебника по курсу для определения требуемых стандартных параметров. При изучении дисциплины необходимо разобраться в методах решения инженерных задач, уметь анализировать используемые расчетные формулы, уяснить работу как отдельной детали или узла машины, так и устройства в целом. При расчетах следует обратить внимание на правильность выбора материалов, определение допускаемых напряжений и коэффициентов запаса прочности. “ Прикладная механика ” Руководство к решению контрольных задач по дисциплине и примеры решения задач Авторы: Белоконев К.И. Гафнер С.Л. Коровин Е.К. Москалев В.Н. Под редакцией докт. техн. наук, проф. В.Г. Дмитриева Москва МГОУ, 2009 год СОДЕРЖАНИЕ Стр. Раздел 1. Задачи по сопротивлению материалов………. 4 Раздел 2. Задачи по теории механизмов и машин………. 10 Раздел 3. Задачи по деталям машин ……………………… 16 Приложения ………………………………………………… 30 РАЗДЕЛ 1. ЗАДАЧИ ПО СОПРОТИВЛЕНИЮ МАТЕОИАЛОВ. В разделе приведены методики расчета и построения эпюр моментов, усилий и деформаций при кручении и изгибе. При решении задач используется метод сечений ,при котором рассматривается равновесие отсеченной части при действии моментов и усилий. Реакции в опорах определяются по уравнениям статики . Задача 1.1. К стальному ступенчатому валу, имеющему сплошное сечение, приложены четыре крутящих момента (рис. 1.1). Левый конец вала жестко закреплен в опоре, а правый конец – свободен и его торец имеет угловые перемещения относительно левого конца 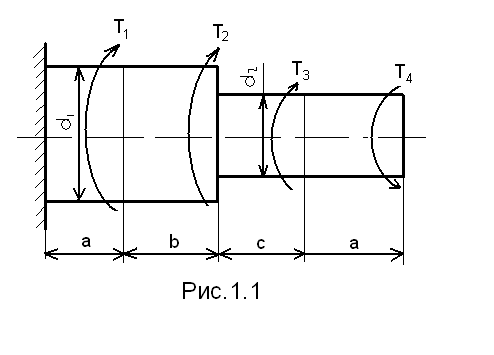 При решении задачи требуется: Построить эпюру крутящих моментов по длине вала; При заданном значении допускаемого напряжения на кручение определить диаметры d1 и d2 вала из расчета на прочность, полученные значения округлить; Построить эпюру действительных напряжений на кручение по длине вала; Построить эпюру углов закручивания. Исходные данные: a =1,0 м; b =1,0 м; с =1,0 м; T1 =5,5 кН.м; T2 =2,5 кН.м; T3 = 1,5 кН.м; T4 = 0.5 кН.м; [τк] =40 МПа. Последовательность решения задачи Построение эпюры крутящих моментов ( рис.1.2 ). Построение эпюры начинаем от свободного конца. Направление вращения по часовой стрелке принимаем за положительное. На участке IV: Tк4 = - T4 =-0,5 кН·м На участке III: Tк 3= T3-T4= 1,5 -0,5= 1 кН·м На участке II: Tк 2= T2+T3-T4= 2,5+1,5-0,5= 3,5 кН·м На участке I: Tк1 = T1+T2+T3 - T1 =5,5+2,5+1,5-0,5=9 кН·м При построении эпюры крутящих моментов на границах участков вала откладываем полученные значения ( с учетом знака) и соединяем их горизонтальными линиями . 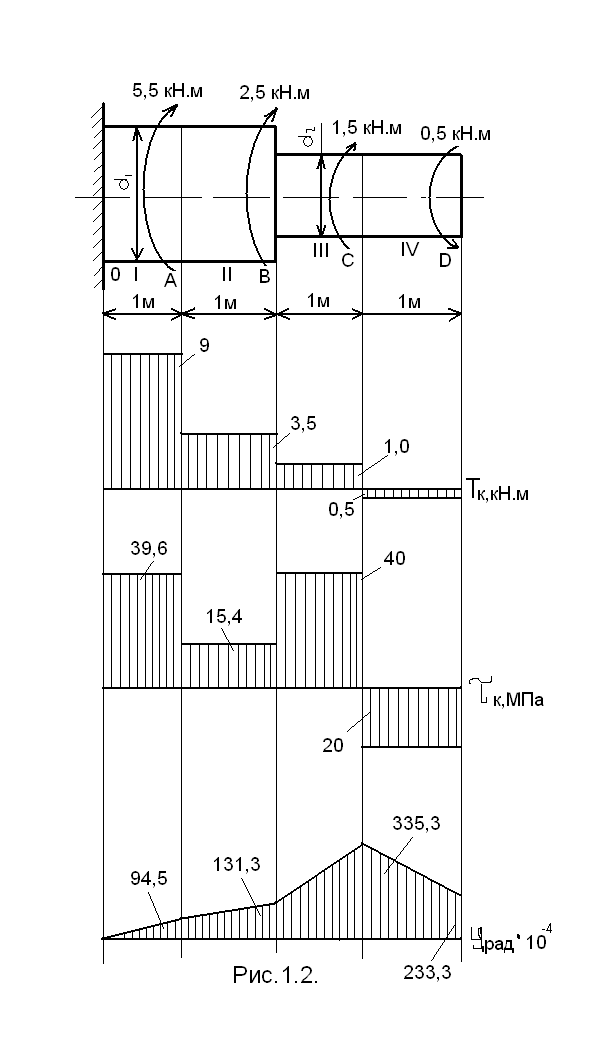      2)Определение диаметров d1и d2. Диаметры валов определяются по уравнению: 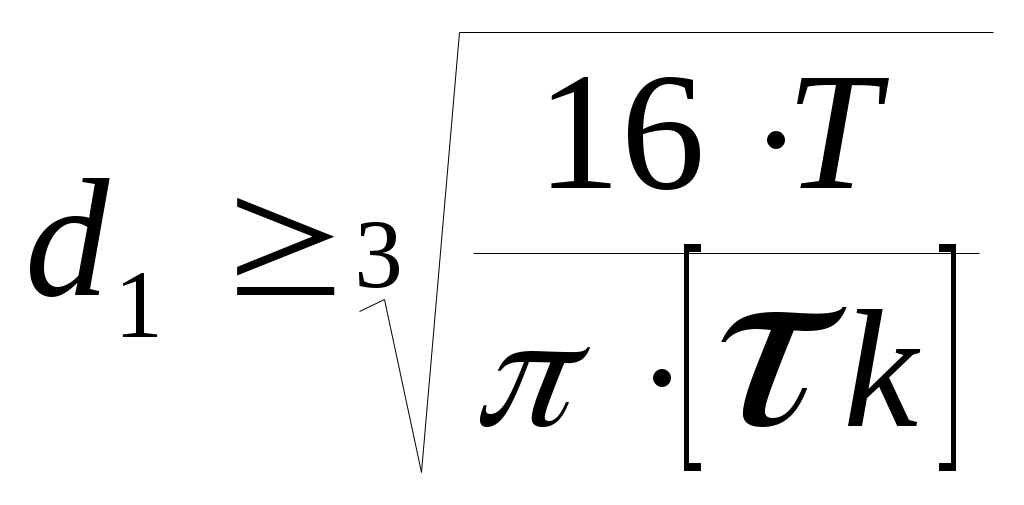 На ступени диаметра d1 : Наибольший крутящий момент Tк1= 9 кН·м. отсюда:  Примем : d1 = 105мм. На ступени диаметра d2: Наибольший крутящий момент Tк3 =1 кН·м. отсюда:  Примем: d2=50 мм. 3)Построение эпюры напряжений на кручение по длине вала. Напряжение на кручение определяется по уравнению:  где wp – полярный момент сопротивления;   На ступени диаметра d1:  На ступени диаметра d2:  Определяем значения напряжений на кручение по участкам: На участке IV:  На участке III:  На участке II:  На участке I:  Полученные результаты откладываем на границах участков и соединяем горизонтальными линиями. Обратите внимание, что наибольшие значения напряжений на обеих ступенях вала должны быть близки друг другу и равны либо несколько меньше значения допускаемого напряжения [τк] . 4) Построение эпюры углов закручивания. Построение эпюры углов закручивания начинаем с сечения 0, где деформация отсутствует. Угол закручивания определяется по уравнению:   , где: l– длина участка, на котором действует крутящий момент; G – модуль упругости при сдвиге, G=0,4Е (Е – модуль упругости при растяжении; Е=2·1011Н/м2) или G=0,8·1011Н/м2; Iр – полярный момент инерции;  На ступени диаметра d1:  На ступени диаметра d2:  Углы закручивания: Сечения А:  Сечения В:  Сечения С:  Сечения D:  На границах сечений откладываем полученные численные значении и соединяем их прямыми линиями. Задача 1.2. Для балки (рис. 1.3) требуется написать выражение поперечных сил F и изгибающих моментов M для каждого участка в общем виде, построить эпюры F и М, найти Мmax и подобрать стальную балку двутаврового поперечного сечения (см. таблицу 1) при 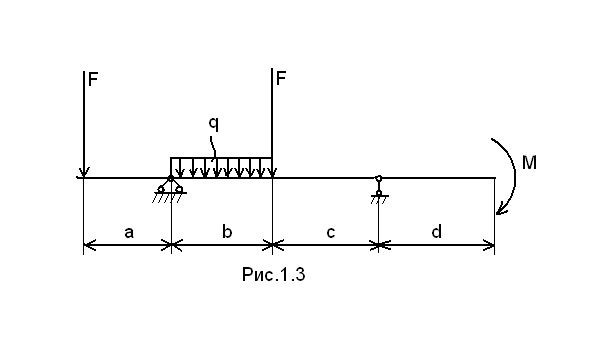 . Исходные данные: а = b = c = d = 1м, сосредоточенная сила F=15 кН, равномерно распределенная нагрузка q =1 5 кН/м, изгибающий момент М =10 кН·м. Последовательность решения задачи 1) Определение реакций в опорах А и В Первоначально принимаем направление реакций в опорах А и В (FА и FВ) вертикально вверх. Величины реакций определяем из условий: ΣМА=0; ΣМВ=0. Распределенную нагрузку заменяем ее равнодействующей, которая равна произведению интенсивности нагрузки q на длину участка, на котором она действует ( Fq ), а точка приложения этой нагрузки, для равномерно распределенной нагрузки, находится на середине участка ее действия. При определении моментов будем считать, что если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то такой момент положительный.     Проверка: ΣY = 0; -F+FA-(q·b)-F+FB=-15+8,75-15-15+36,25 = 0 Реакции определены верно. Составление выражения поперечных сил F На участке I: FI=-F=-15кН На участке II: FII=-F+FA-q(x-a), при x=a FII=-15 +36,25=21,25кН, при x=a+b FII=-15+36,25-15·1=6,25кН. На участке III: FIII=-F+FA-q·b-F=-15+36,25-15-15=-8,75кН На участке IV поперечные силы отсутствуют. 3) Построение эпюры поперечных сил F ( рис.1.4 ) Эпюру поперечных сил строим по полученным в разделе 2 значениям. На участке II значения поперечной силы ввиду действия равномерно распределенной нагрузки зависят от расстояния Х, поэтому получим наклонную прямую. 4) Составление выражения изгибающих моментов При решении принимаем, что если любое из силовых воздействий стремится повернуть левую часть балки по часовой стрелке (а правую – против часовой стрелки), то значение момента будет положительным. Начинаем составлять выражение слева, от участка I. На участке I: MI=-F·x при х=0; MI=0 · при х = а; MI=-F·а=-15·1=- 15 кН.м 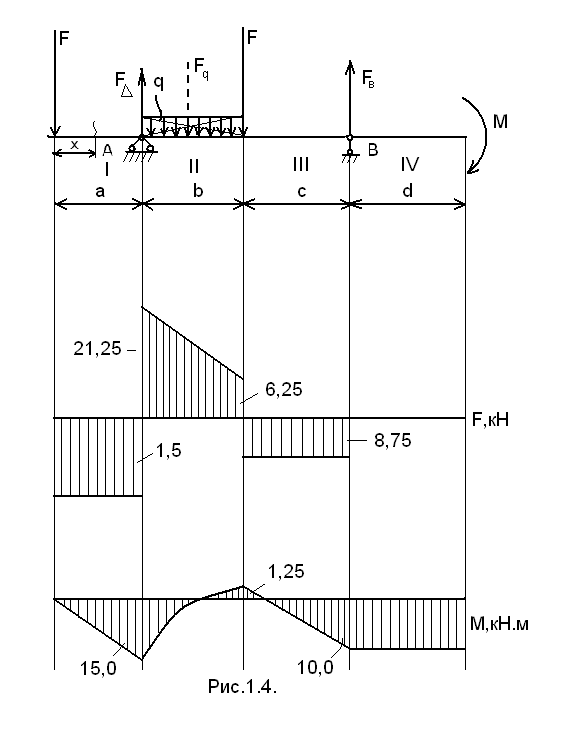  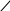     На участке II: MII=-F·x+FA(x-a)-q(x-a) ·  при х=а; MII=-F·а=-15 кН·м. при х=а+b; MII= -F·(а+b)+ FA·b-q·b2/2=-15·2+36,25·1-15·0,5=1,25 кН·м. На участке III: MIII=-F·x+ FA·(x-a) -q·b(x -а-b/2)-F(х -а-b) при х=а+b; MIII= -F·(а +b)+ FA·b-q·b/2=1,25 кН·м. при х=а+b+с; MIII= -F·(а+b+с)+ FA·(b+с)-qb(b/2+с)-F·c=-15·3+36,25-15·1=-10 На участке IV (составляем управление справа налево) MIV=-M= -10 кН·м. На границе участков III и IV значение М совпадает, что говорит о правильности расчета. 5) Построение эпюры изгибающих моментов Полученные в разделе 4 значения откладываем на границах участков. Если на участке балки нет распределенной нагрузки, то два соседних значения изгибающих моментов соединяются прямой линией, а при наличии распределенной нагрузки – по параболе. В месте приложения изгибающего момента - вертикальный скачок на величину этого момента. 6) Подбор балки. Для определения размеров балки воспользуемся уравнением  ;Максимальный изгибающий момент Mmax=15 кН·м .  Этому условию удовлетворяет двутавровая стальная балка ( ГОСТ 8239 – 72) №16, у которой  =109  (см. таблицу 1).РАЗДЕЛ 2. ЗАДАЧИ ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН. 2.1. Определение величины степени подвижности и определение класса механизма. Целью решения задач по данной теме является выработка навыков структурного анализа кинематических цепей механизмов. В результате структурного анализа устанавливается: являются ли анализируемые кинематические цепи механизмами, из каких структурных групп – с установлением их классов и, если требуется, видов – образованы анализируемые кинематические цепи [1]. 2.1.1. Порядок выполнения работы. Вычерчивают структурную схему исследуемой кинематической цепи. Звенья обозначают цифрами, а кинематические пары – латинскими буквами. Составляют таблицу кинематических пар, определяя какие звенья, образуют кинематические пары. Например: A (0 – 1), B (2 – 5) и т.д. определяют степень подвижности кинематической цепи и сравнивают её значение с числом входных звеньев, делая вывод – является ли кинематическая цепьмеханизмом. При необходимости выполняют замену высших кинематических пар, условно удаляя звенья, создающие пассивные связи, не влияющие на подвижность кинематической цепи. После этого определяют степень подвижности заменяющей кинематической цепи и сравнивают её значение с числом входных звеньев, делая вывод – является ли кинематическая цепьмеханизмом. Вычерчивают структурную схему кинематической цепи заменяющего механизма. Из кинематической цепи механизма – руководствуясь признаком структурной группы  , выделяют кинематические цепи составляющих её структурных групп, вычерчивая их схемы.Для каждой структурной группы определяют её класс и порядок, и – при необходимости – вид. Определяют класс механизма. Пример. Для заданной схемы плоской кинематической цепи определить величину степени подвижности и сделать вывод – является ли кинематическая цепь механизмом. Если кинематическая цепь является механизмом, определить его класс. 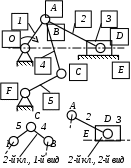 Последовательность решения задачи. Обозначим звенья кинематической цепи цифрами, а кинематические пары – латинскими буквами. Таблицу кинематических пар заполняют, определяя какие звенья их составляют, и их класс: O(0–1) кл. 5, A(1–2) кл. 5, B(2–4 кл. 5) и т.п. Обозначения звеньев и кинематических пар наносят на схему. В примере номера звеньев и обозначения кинематических пар на схеме заключены в рамки, чтобы обратить внимание на то, что их помещают на схему при решении. При выполнении заданий рамки не проставляют. Так как кинематическая цепь – плоская, то её степень подвижности определим по формуле Чебышева:  . Для заданной цепи  . Следовательно,  . Так как величина W совпадает с заданным числом входных звеньев (они обозначены на схемах стрелками), то заданная кинематическая цепь является механизмом. По правилам структурного анализа выделим структурные группы из кинематической цепи механизма. Их схемы с обозначенными звеньями и кинематическими парами вычерчивают без соблюдения масштаба, определяют их класс и вид. Класс механизма определяют по наивысшему классу структурной группы. Данный механизм – второго класса. 2.2. Кинематика зубчатых механизмов. При кинематических расчётах зубчатого механизма определяют либо угловые скорости звеньев механизма, на которых установлены зубчатые колёса, либо передаточные отношения между входным звеном и промежуточными или выходными звеньями механизма. кинематический расчёт зубчатого механизма начинают с анализа его работы, определения характера движения его звеньев, определения к каким звеньям относятся зубчатые колёса механизма. При этом следует помнить, что: кинематический расчёт зубчатого механизма с неподвижными осями зубчатых колёс (рядового механизма) можно выполнить по соотношениям чисел зубьев пар зацепляющихся колёс; кинематический расчёт зубчатого механизма с подвижными осями зубчатых колёс можно выполнить только с использованием формулы Виллиса. Изучив работу механизма, необходимо нарисовать его кинематическую схему, используя стандартные символы для обозначения зубчатых колёс, способа их соединения с валами и осями механизма. Следует помнить, что конструктивная и кинематическая схемы механизма – это не одно и то же, что зубчатые колёса, как правило, не являются звеньями механизма, а звенья представляют совокупность валов и жёстко соединённых с ними зубчатых колёс. 2.2.1. Порядок выполнения работы. После анализа кинематической схемы механизма необходимо определить: числа зубьев зубчатых колёс механизма (в большинстве моделей они написаны на торцевых плоскостях зубчатых колёс); степень подвижности механизма по его кинематической схеме – если её величина совпадает с числом входных звеньев, то схема соответствует модели механизма; передаточное отношение зубчатого механизма либо угловые скорости звеньев –в зависимости от типа механизма. П  ример. Выполнить кинематический расчёт приведеного на схеме многозвенного сателлитного дифференциального механизма с двумя входными звеньями 1 и 3. Действуя в указанной выше последовательности, запишем формулу Виллиса для колес 1 и 3, угловые скорости которых заданы:  . ( 2.1.)Передаточное отношение обращенного механизма получим через числа зубьев зубчатых колес: 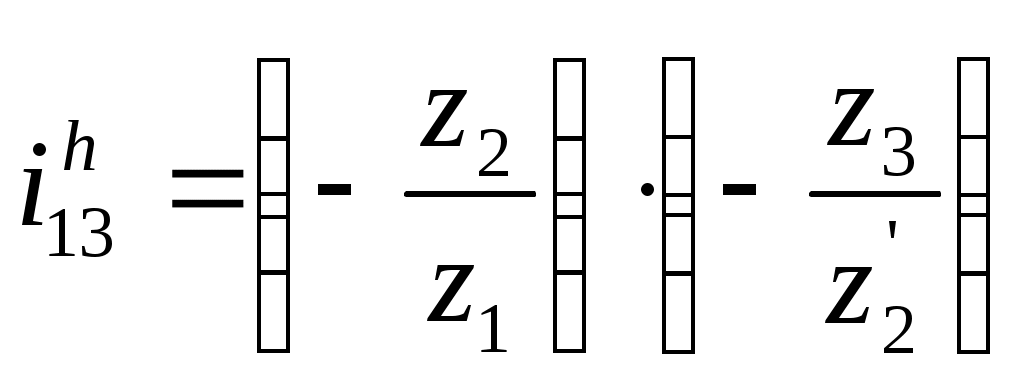 . Решая уравнение (2. 1.) относительно ωh, получим величину угловой скорости водила. Если затормозить колесо 3, – то есть ω3 = 0, то механизм перестает быть дифференциальным. Тогда выражение (2. 1.) примет вид 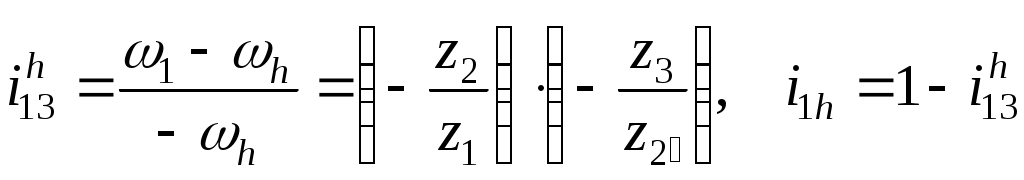 . (2. 2.)Такие сателлитные механизмы теоретически позволяют реализовать любое передаточное отношение путем подбора зубьев. Например, задаваясь числами зубьев зубчатых колес z1 = 100, z2 = 101, z2' =100, z3 = 99, получим 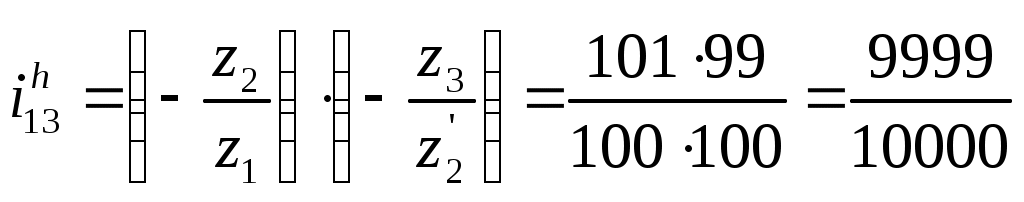 .поделив числитель на знаменатель в выражении (2. 2), получим  .Следовательно, колесо 1 будет вращаться в 10000 раз медленнее водила h. Для получения такого передаточного отношения в рядовом зубчатом механизме потребуется несколько пар зубчатых колес, и он будет иметь большие габаритные размеры. Из формулы (2.2.) следует, что в сателлитных механизмах с одним входным звеном из формулы Виллиса можно получить зависимость для определения передаточного отношения между любым колесом и водилом. Для определения передаточного отношения между зацепляющимися колесами механизма нельзя воспользоваться просто отношением их чисел зубьев, так как оси колес подвижны. В этом случае необходимо предварительно определить передаточное отношение между каждым колесом и водилом, а затем – передаточное отношение между колесами. Например, если требуется определить передаточное отношение i12, то следует выполнить следующие преобразования: 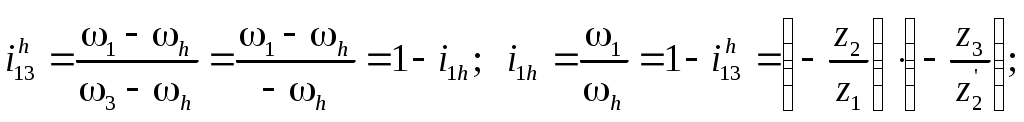 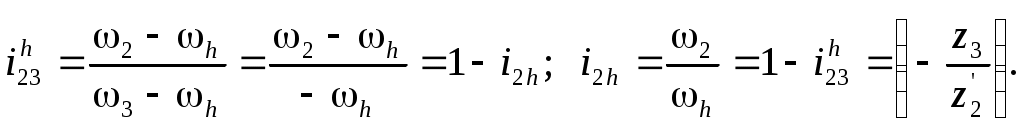 Тогда  , то есть в сателлитном механизме передаточное отношение между различными колесами равно отношению передаточных отношений между этими колесами и водилом. Если зубчатый механизм включает сателлитную и рядовую ступени, то его передаточное отношение равно произведению передаточных отношений ступеней. Для сателлитной ступени передаточное отношение определяется из формулы Виллиса, а для рядовой – через отношение чисел зубьев. Например, для приведенной схемы такого механизма получим: 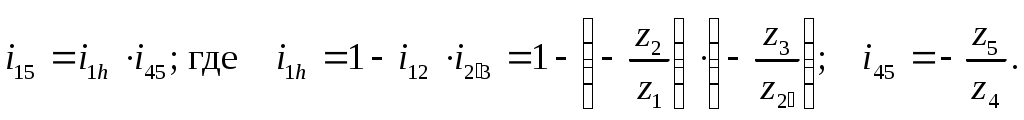 2.3.Силовой расчет. Силовой расчёт выполняется для той же схемы механизма, для которой выполнялся кинематический расчёт. При силовом расчёте используют значения кинематических параметров, полученные при кинематических расчётах. 2.3.1. Порядок выполнения работы. Силовой расчёт выполняется для той же схемы механизма, для которой выполнялся кинематический расчёт. При силовом расчёте используют значения кинематических параметров, полученные при кинематических расчётах. .Пример.Для главного вектора системы сил звена задают его величину F, направляющий угол γ. Координаты точки приложения главного вектора задают величиной и направляющим углом её радиус-вектора, если её координаты неизвестны из кинематического расчёта механизма. Целесообразно начало радиус-вектора помещать в точку, относительно которой будут составляться уравнения моментов при рассмотрении равновесия звеньев. главный момент систем сил каждого звена задают парой сил с учётом знака. 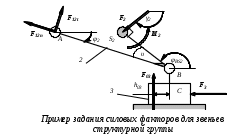 Силовой расчёт выполняется в два этапа. На первом этапе работы с соблюдением масштаба вычерчивается кинематическая схема механизма для того же положения входного звена, для которого выполнялся кинематический расчёт механизма. В том же масштабе вычерчивается схема структурной группы, входящей в механизм. К звеньям структурной группы прикладывают главный вектор и главный момент систем сил, действующих на каждое звено (см. рисунок). Линейные и угловые координаты радиус-векторов точек приложения главных векторов либо задаются численно, либо снимаются с чертежа. Если какой либо из силовых факторов не задан, то при работе его величина задаётся как ноль. По заданным исходным данным выбирают значение обобщённой координаты входного звена, для которого выполняют силовой расчёт четырёхзвенного механизма. Построения сопровождают вычислениями необходимых величин, векторными уравнениями с необходимыми пояснениями. используя векторные условия равновесия структурных групп и их звеньев, определяют реакции в кинематических парах в соответствии с исходными данными, результатами кинематических расчётов механизма и заданными силовыми факторами. Для выбранного положения звеньев записывают векторные уравнения равновесия сил и моментов сил. После решения уравнения моментов сил и векторных уравнений равновесия определяют модули, направляющие углы реакций и координаты точек приложения их в поступательных кинематических парах структурной группы. Необходимо помнить о том, что все угловые координаты векторов сил необходимо отсчитывать от горизонтали с учётом знака. |