FreeFEM_Стационарнаятеплопроводность. Теплопроводность с источником теплоты. Теплопроводность с источником теплоты Рассматривается
 Скачать 109.17 Kb. Скачать 109.17 Kb.
|
|
Теплопроводность с источником теплоты Рассматривается задача теплопроводности с источником теплоты в заданной области. Необходимо найти распределение температур в области, среднеобъемную температуру, среднеповерхностную температуру. Модель реализуется в программном пакете FreeFem++. Заданная область: 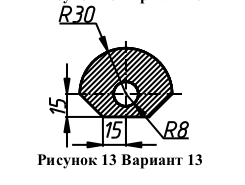 Параметры области: W = 30кВт/м2 =30000 Вт/м2 мощность источника ta = 25 C = 298 К температура окруж среды alpha = 9 Вт/м2К коэфф-т теплоотдачи lyambda = 16 Вт/мК коэфф-т теплопроводности В общем виде линейная двумерная стационарная задача теплопроводности описывается следующим дифференциальным уравнением в частных производных в некоторой области D на плоскости (x, y): 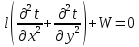 l– коэффициент теплопроводности W – объемная плотность мощности источников теплоты внутри тела Для нашего случая будем пользоваться граничным условием первого рода: 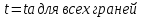 Тогда вариационную формулировку для этой задачи можно записать в FreeFem++ как: solve cond1(t,phi)= int2d(D)(lam*(dx(t)*dx(phi)+ dy(t)*dy(phi)))-int2d(D)(W*phi) + on(g1,g2,g3,g4,g5,g6, t= ta) Результаты: Изображение полученной сетки: 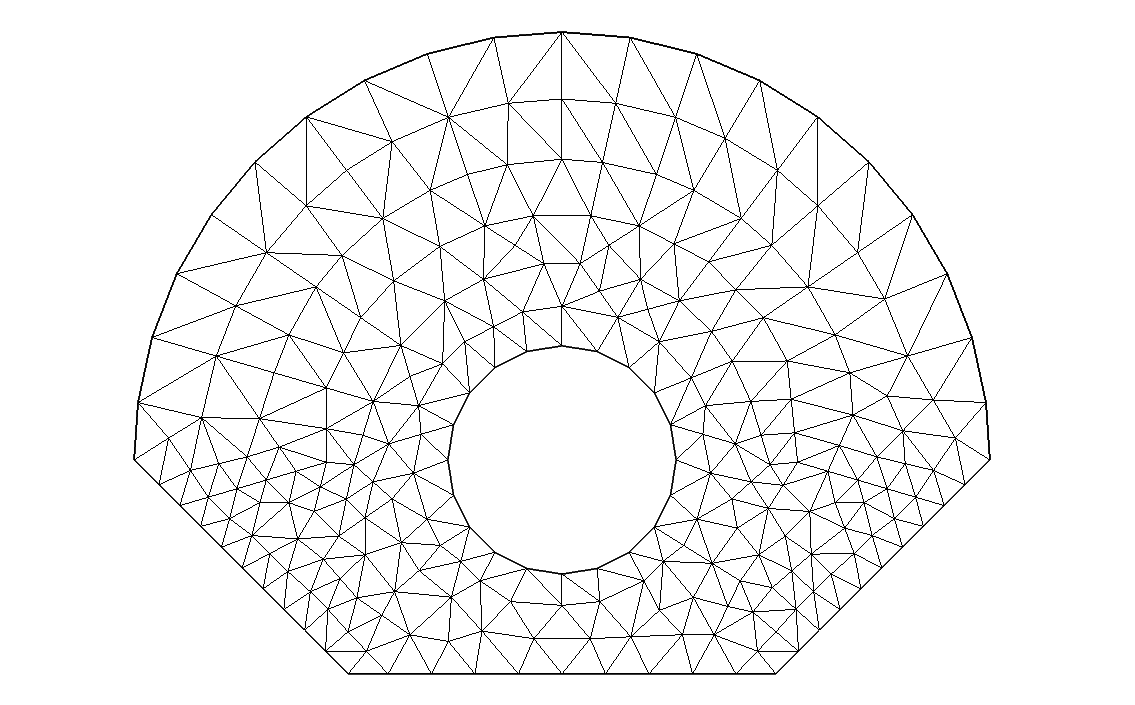 Изображение распределения коэфф-та теплопроводности (lya = const):  Распределение объемной мощности (W=const):  Полученное распределение температуры:  Полученные значения среднеобъемной и среднеповерхностной температур: Вывод: Таким образом, мы изучили методы численного решения задачи теплопроводности с источником теплоты и получили результаты в программном пакете FreeFem++ |
