Теория. Тепловое излучение
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
Второй постулат (правило частот): излучение и поглощение энергии в виде кванта света (hn) происходит лишь при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается скачок электрона: 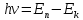 Правило квантования орбит: из всех орбит электрона возможны только те, для которых момент импульса равен целому кратному постоянной Планка: 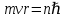  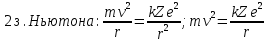 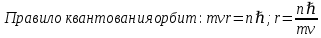 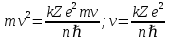 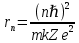 Внутренняя энергия атома слагается из кинетической энергии электрона (ядро неподвижно) и потенциальной энергией взаимодействия электрона с ядром: 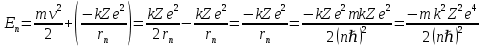 При Z=1 – атом водорода 20. Закономерности спектра атома водорода. Спектральные серии. Спектральная формула. Изолированные атомы в виде разреженного газа или паров металлов испускают спектр, состоящий из отдельных спектральных линий (линейчатый спектр). Расстояние между линиями в серии закономерно уменьшается по мере перехода от длинных волн к коротким. 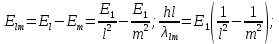 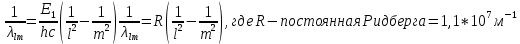 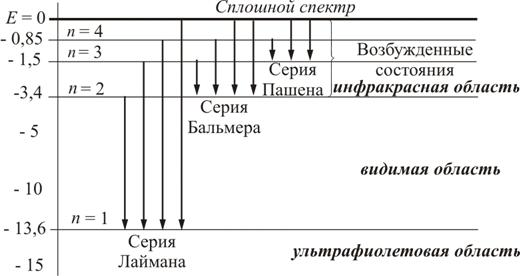 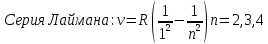 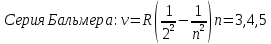 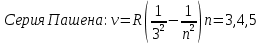 21. Корпускулярно- волновой дуализм. Гипотеза и формула де-Бройля. Опыты, подтверждающие гипотезу де Бройля. Корпускулярно-волновой дуализм – свойство любой микрочастицы обнаруживать признаки частицы и волны. Гипотеза : Корпускулярно-волновой дуализм присущ не только свету, но и частицам. Если фотон обладает энергией и импульсом , то и частица (например электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е. движение частицы можно рассматривать как движение волны. Согласно квантовой механике, свободное движение частицы с массой m и импульсом р=mv (где v – скорость частицы) можно представить как плоскую монохроматическую волну (волну де Бройля) с длиной волны : 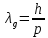 Опыт : дифракция электронов на кристаллах - рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц. 22. Соотношение неопределенностей Гейзенберга для координат и импульса. Невозможность описания поведения частиц с помощью классического понятия траектории. Произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга. 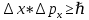 Чем меньше неопределенность одной величины, тем больше неопределенность другой. Возможно, такое состояние, в котором одна их переменных имеет точное значение (=0), другая переменная при этом оказывается совершенно неопределенной ( ее неопределенность равна бесконечности), и наоборот. Для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременного измерения координаты и импульса микрообъекта с любой наперед заданной точностью. Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. 23. Соотношение неопределенностей Гейзенберга для энергии и времени. Оцените с помощью соотношения неопределенностей естественную ширину спектральной линии излучения атома. 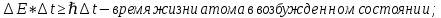 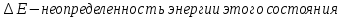 Естественная ширина спектральной линии обусловлена неопределенностью значения энергии в возбужденном состоянии. 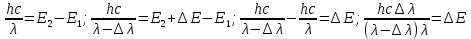 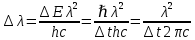 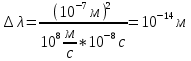 24. Волновая или 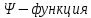 частицы и ее вероятностный смысл . Смысл условия нормировки волновой функции. частицы и ее вероятностный смысл . Смысл условия нормировки волновой функции.Состояние микрочастицы описывается с помощью волновой функции 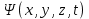 . . Квадрат модуля волновой функции определяет вероятность нахождения данной частицы в данный момент времени в окрестностях данной точки. 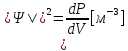 - Вероятность того, что частица в момент времени t находится в точке с координатами (x, y, z) и в кубе со сторонами dx, dy, dz : dV=dx*dy*dz - Вероятность того, что частица в момент времени t находится в точке с координатами (x, y, z) и в кубе со сторонами dx, dy, dz : dV=dx*dy*dzСвойства: конечна (вероятность не может быть больше единицы), неоднозначна (вероятность не может быть неоднозначной величиной), непрерывна (вероятность не может меняться скачком) Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме о сложении вероятностей, равна: 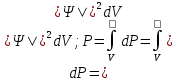 Т.к. 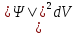 определяется как вероятность, то необходимо волновую функцию определяется как вероятность, то необходимо волновую функцию 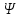 представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей: представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей: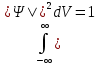 - где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от -∞ до ∞ . Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве. - где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от -∞ до ∞ . Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве.25. Уравнение Шредингера для стационарных состояний для частицы массой m в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Выражение для 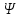 -функции этой частицы. -функции этой частицы.Уравнение Шредингера , уравнение из которого находится волновая функция; постулировано. Стационарное состояние – состояние с определенными значениями энергии. Одномерная потенциальная яма описывается потенциальной энергией U (x) следующего вида: 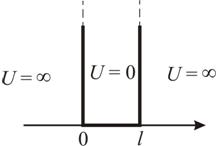 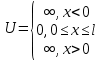 Уравнение Шредингера для стационарных состояний в случае одномерной задачи : 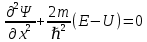 По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. На границах ямы волновая функция также должна обращаться в нуль: 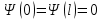 В пределах ямы ( 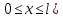 ) уравнение Шредингера: ) уравнение Шредингера: 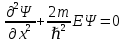 или или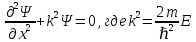 Общее решение дифференциального уравнения: 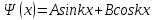 Т. к. 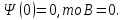 Тогда : Тогда : 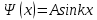 Уравнение 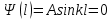 выполняется только при выполняется только при 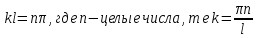 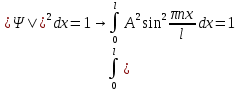 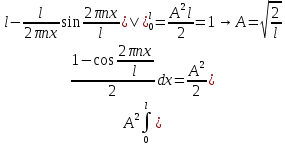 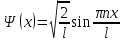 26. Уравнение Шредингера для стационарных состояний для частицы массой m в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Получите выражение для энергии частицы. Уравнение Шредингера для стационарных состояний в случае одномерной задачи : 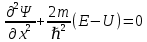 По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. На границах ямы волновая функция также должна обращаться в нуль: 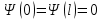 В пределах ямы ( 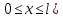 ) уравнение Шредингера: ) уравнение Шредингера: 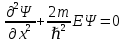 или или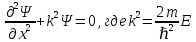 Общее решение дифференциального уравнения: 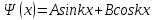 Т. к. 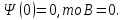 Тогда : Тогда : 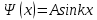 Уравнение 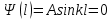 выполняется только при выполняется только при 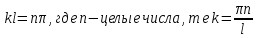 Энергия частицы зависит от n: 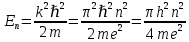 Энергия En частицы в потенциальной яме с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии En называются уровнями энергии, а число n, определяющее энергетические уровни – главным квантовым числом. 27. Уравнение Шредингера для стационарных состояний для частицы массой m в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Выражение для 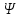 -функции частицы. Найдите максимальное значение плотности вероятности нахождения частиц в потенциальной яме. -функции частицы. Найдите максимальное значение плотности вероятности нахождения частиц в потенциальной яме.Уравнение Шредингера для стационарных состояний в случае одномерной задачи : 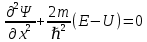 По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. На границах ямы волновая функция также должна обращаться в нуль: 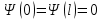 В пределах ямы ( 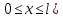 ) уравнение Шредингера: ) уравнение Шредингера: 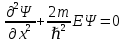 или или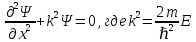 Общее решение дифференциального уравнения: 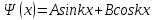 Т. к. 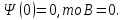 Тогда : Тогда : 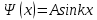 Уравнение 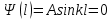 выполняется только при выполняется только при 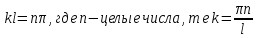 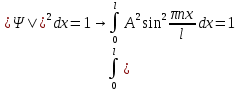 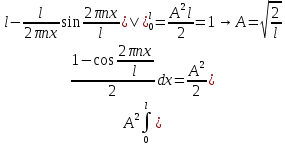 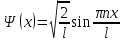 Максимальное значение плотности вероятности нахождения частиц в потенциальной яме: 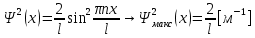 28. Уравнение Шредингера для стационарных состояний для частицы массой m в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Покажите , что в стационарных состояниях на ширине ямы укладывается целое число полуволн де Бройля частицы. Уравнение Шредингера для стационарных состояний в случае одномерной задачи : 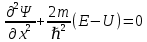 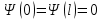 В пределах ямы ( 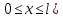 ) уравнение Шредингера: ) уравнение Шредингера: 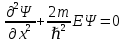 или или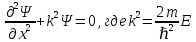 Общее решение дифференциального уравнения: 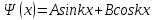 Т. к. 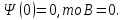 Тогда : Тогда : 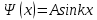 Уравнение 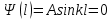 выполняется только при выполняется только при 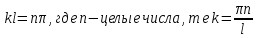 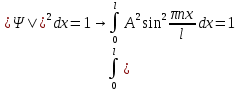 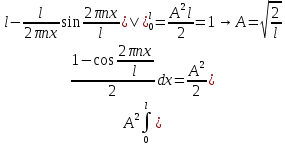 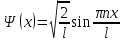 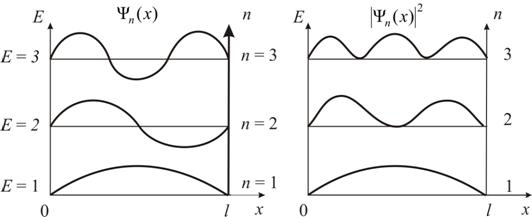 А) Графики собственных функций , соответствующие уровням энергии Б) Плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы Например, в квантовом состоянии с п = 2 частица не может находиться в центре ямы, в то время как одинаково может пребывать в ее левой и правой частях. 29. Уравнение Шредингера для гармонического осциллятора. Значения энергии осциллятора. Минимальная энергия осциллятора. Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы 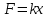 Потенциальная энергия частицы : 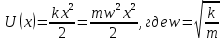 Уравнение Шредингера: 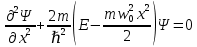 Полная энергия осциллятора : 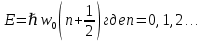 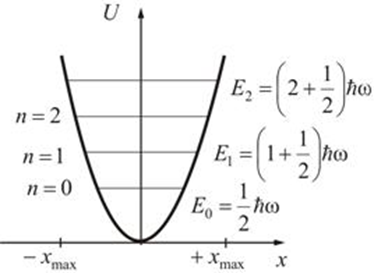 30. Используя соотношения неопределенностей для координат и импульса, оцените минимальную энергию частицы массой m , находящейся в бесконечной прямоугольной потенциальной яме шириной l. 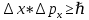 Неопределенность импульса на отрезке 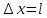 составляет составляет 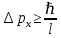 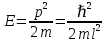 31. Напишите уравнение Шредингера и его решение для электрона в атоме водорода в основном состоянии. Главное квантовое число n. Плотность вероятности нахождения электрона на расстоянии r от ядра(радиальная плотность вероятности). Нарисуйте график зависимости этой плотности вероятности от r для n=1 Потенциальная энергия взаимодействия электрона с ядром: 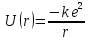 Уравнение Шредингера для атома водорода : 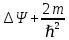 (E + (E +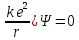 Решение : 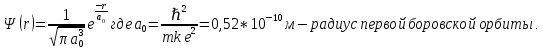 n– главное квантовое число, определяющее энергетические уровни. Радиальная плотность вероятности - плотность вероятности нахождения электрона в шаровом слое толщиной dr на заданном расстоянии от ядра r . 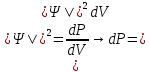 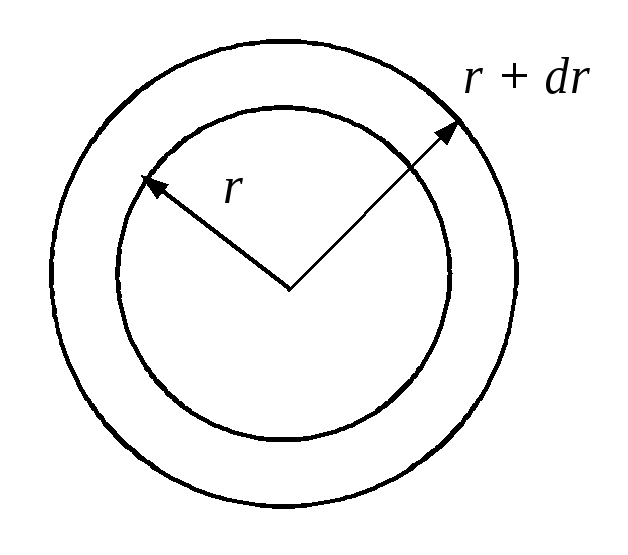 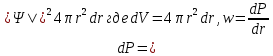 32. Представление волновой функции, являющейся решением уравнения Шредингера для электрона в атоме водорода, в произведении радиальной и угловой частей. Квантование момента импульса. Орбитальное и магнитное квантовые числа. Непрерывные, однозначные и конечные решения уравнения Шредингера для электрона в атоме водорода содержат 3 целочисленных параметра n, l, m 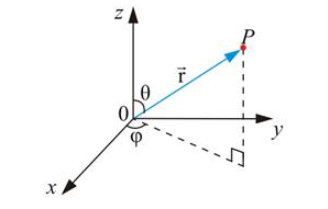 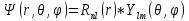 n- главное квантовое число , номер уровня энергии, n=1, 2, 3, … l – орбитальное квантовое число, определяет модуль орбитального момента импульса электрона Момент импульса электрона : 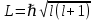 , l= 0, 1, 2,…, n-1 , l= 0, 1, 2,…, n-1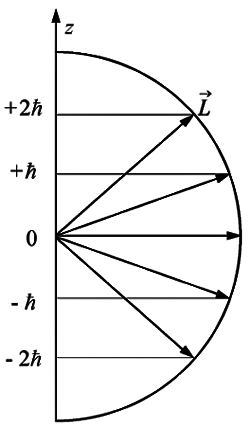 m- магнитное квантовое число, определяет проекцию орбит момента импульса на направление внешнего магнитного поля; m- магнитное квантовое число, определяет проекцию орбит момента импульса на направление внешнего магнитного поля; 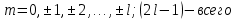 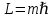 Если l=2 Квантовые числа – следствия решений уравнения Шредингера Пространственное квантование: момент импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция на направляющую внешнего магнитного поля принимает квантованные значения, кратные 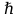 33. Механический и магнитный моменты орбитального движения электрона в атоме и их проекции на направление внешнего поля. Магнетон Бора. Гиромагнитное отношение для орбитального движения электрона . 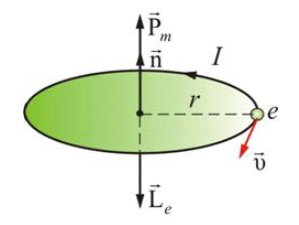 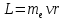 -импульс на плечо -импульс на плечо Для витка : 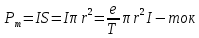 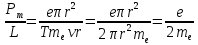 - орбитальное, гиромагнитное отношение (отношение магнитного момента к механическому ) - орбитальное, гиромагнитное отношение (отношение магнитного момента к механическому )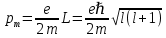 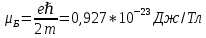 - магнетон Бора - магнетон Бора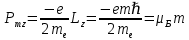 34. Спин и собственный момент электрона и их проекции на направление внешнего поля. Спин обнаружен в опытах Штерна и Гермаха. Пучок электронов в s-состоянии ( орбитальное квантовое число =0, L=0) , проходя область сильно неоднородного магнитного поля расщепляется на 2 пучка, это свидетельствует о наличии у электронов собственного магнитного момента и двух его возможных ориентаций. 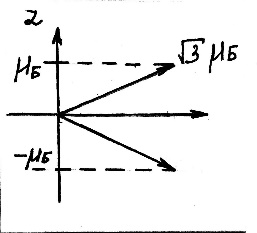 Спин- собственный неустойчивый момент импульса , не связанный с движением электрона в пространстве. Спин-квантовая величина , у которой нет классических аналогов. Спин- собственный неустойчивый момент импульса , не связанный с движением электрона в пространстве. Спин-квантовая величина , у которой нет классических аналогов.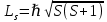 S-спиновое квантовое число ; 2S+1 – количество возможных ориентаций спина S-спиновое квантовое число ; 2S+1 – количество возможных ориентаций спина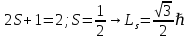 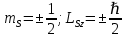 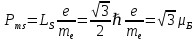 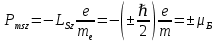 Правило отбора : Возможны лишь те переходы, при которых орбитальное квантовое число меняется на единицу , а магнитное квантовое число или не меняется или меняется на единицу 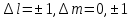 l=0 l=1 l=2 l=3 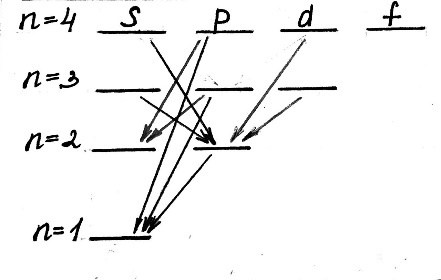 35. Квантовые числа 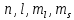 и их связь с физическими характеристиками состояния электрона. и их связь с физическими характеристиками состояния электрона.Состояние электрона в атоме определяется набором четырех квантовых чисел. n-главное квантовое число; n = 1, 2, … ∞ ; определяет уровни энергии электрона в атоме водорода(энергию 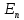 электрона) электрона)l-орбитальное квантовое число, характеризует подуровень, определяет форму электронного облака и показывает запас энергии на подуровне ; l = 0, 1, 2, … n-1; характеризует орбитальный момент импульса электрона относительно ядра : 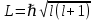 m - магнитное квантовое число; возможны лишь такие ориентации L, при которых проекция Lz вектора L по направлению Z внешнего магнитного поля принимает значения, кратные 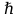 : Lz = m : Lz = m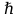 где m принимает значения: m = 0, ±1, ±2,…,±l ; для спинового момента электрона, протона, нейтрона, кварка где m принимает значения: m = 0, ±1, ±2,…,±l ; для спинового момента электрона, протона, нейтрона, кварка 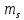 = ±1/2 = ±1/2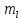 – магнитное орбитальное квантовое число определяет ориентацию – магнитное орбитальное квантовое число определяет ориентацию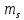 - спиновое магнитное квантовое число = ±1/2; характеризует возможные проекции на ось z собственного механического момента электрона. - спиновое магнитное квантовое число = ±1/2; характеризует возможные проекции на ось z собственного механического момента электрона.36. Квантовые числа. Максимальное число электронов , находящихся в состояниях , определяемых главным квантовым числом n. 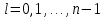 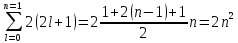 37. Принцип Паули. Последовательность заполнения электронами энергетических оболочек атомов. Нарушения этой последовательности. Принцип Паули : В одном атоме не может быть больше одного электрона с определенным набором квантовых чисел. 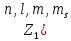 )= 0 или 1, где )= 0 или 1, где 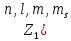 )- число электронов в состоянии, характеризуемом данным набором квантовых чисел. )- число электронов в состоянии, характеризуемом данным набором квантовых чисел.Последовательность заполнения орбиталей атомов, начиная с более низких по энергии, характеризуется тем, что электроны первоначально по одному занимают разные орбитали и имеют параллельные спины. 38. Принцип Паули. Получите выражение для максимального числа электронов в электронных оболочках атомов. Электронная оболочка- совокупность электронов с одинаковым числом n. Подоболочка - это совокупность электронов в каждой оболочке, соответствующих каждому значению 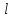 Число подоболочек равно номеру n 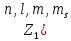 )= 0 или 1, где )= 0 или 1, где 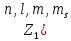 )- число электронов в состоянии, характеризуемом данным набором квантовых чисел. )- число электронов в состоянии, характеризуемом данным набором квантовых чисел.Максимальное число Z2 (n, l, m,) электронов, находящихся в состояниях, описываемых набором трех квантовых чисел и отличающихся только ориентацией спинов Z2(n, l, m,) = 2, так как спиновое квантовое число ms может принимать лишь два значения 1/2 и – 1/2. Максимальное число Z2(n, l) электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l: Z3(n, l) = 2(2l + 1) Максимальное число Z(n) электронов, находящихся в состояниях, определяемых значением главного квантового числа n 
39. Элементы квантовой статистики. Статистика Бозе- Эйнштейна и Ферми-Дирака. Бозоны и фермионы. Тождественные частицы - это частицы с одинаковыми физическими свойствами ( масса, спин, электрический заряд) Принцип неразличимости тождественных частиц: тождественные частицы экспериментально различить невозможно. Рассмотрим систему двух тождественных частиц: 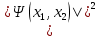 – физический смысл = – физический смысл =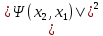 где где 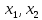 - совокупности пространственной спиновой координаты частиц. - совокупности пространственной спиновой координаты частиц.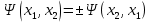 Частицы, описываемые симметричной волновой функцией, называются бозоны, и подчиняются статистике Бозе-Эйнштейна (примеры: фотоны). Бозоны обладают целым спином и могут находиться в одинаковом квантовом состоянии в любом количестве. Антисимметричные частицы, описанные антисимметричной волновой функцией, называются фермионы, и подчиняются статистике Ферми - Дирака . Фермионы обладают полуспином и могут находиться в квантовом состоянии только по одиночке. 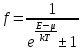 µ- химический потенциал f-среднее число частиц, приходящихся на одно состояние( заселенность уровня) + - относится к Ферми-Дираку – - относится к Бозе-Эйнштейну 40. Модель свободных электронов в металлах. Заселенность энергетического уровня (среднее число электронов, находящихся в квантовом состоянии с энергией 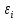 ). Энергия Ферми. Ее смысл при Т=0. ). Энергия Ферми. Ее смысл при Т=0. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
