Информация и информационные процессы. Термин информация происходит от латинского informatio, означающего
 Скачать 287.69 Kb. Скачать 287.69 Kb.
|
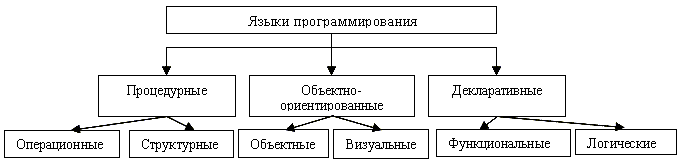
Алгоритм решения задачи, заданный в виде последовательности команд на языке вычислительной машины (в кодах машины), называется машинной программой.Команда машинной программы или машинная команда — элементарная инструкция машине, выполняемая ею автоматически без каких-либо дополнительных указаний и пояснений. Программирование — теоретическая и практическая деятельность, связанная с созданием программ. Процесс перевода алгоритма в машинную программу называетсятрансляцией. Осуществление трансляции силами человека — задача очень сложная в силу большого объема работы и сложности системы команд современных ЭВМ. Поэтому в целях облегчения задачи трансляции появились промежуточные способы задания алгоритмов, получившие название языков программирования. Первоначально появились программы, переводящие символические имена в машинные коды. Затем были созданы программы, транслирующие арифметические выражения и, наконец, в 1958 году появился транслятор Фортрана — первого широко используемого языка программирования. С тех пор было создано множество языков программирования. Как и естественные языки, языки программирования имеют свой алфавит, синтаксис и семантику (смысловое содержание). В зависимости от уровня абстракции понятий, которыми оперируют языки программирования, их принято подразделять на языкинизкого и высокого уровня. Языки программирования, оперирующие понятиями, близкими к исполнителю, называются языками низкого уровня. Наиболее распространенным языком низкого уровня является Ассемблер. Такие языки рассчитаны на определенную архитектуру ЭВМ и на определенный тип процессора. Они позволяют писать быстродействующие программы, которые используют минимальные ресурсы, однако, написание программ на них очень трудоемко. Языки программирования, оперирующие понятиями математической или информационной модели (или близкими к ним) называются языками высокого уровня. Языками высокого уровня являются такие языки, как Паскаль, C++, Бейсик, Java и другие. Языки высокого уровня используются для написания сложных программ, они не привязаны к конкретной архитектуре ЭВМ, значительно легче в изучении и рассчитаны на широкий круг задач. Ряд языков предназначен не для реализации вычислительных алгоритмов, а для «склеивания» частей, реализованных на других языках программирования. Такие языки называются скриптовыми. Существует два основных вида трансляторов языков высокого уровня:интерпретаторы, которые сканируют и проверяют исходный код в один шаг, икомпиляторы, которые сканируют исходный код для производства текста программы на машинном языке, которая затем выполняется отдельно. Интерпретаторы исполняют алгоритм медленнее, однако позволяют программисту контролировать ход исполнения программы, облегчают отладку и предоставляют разработчику ряд уникальных возможностей; Программа на машинном языке, полученная с помощью компилятора, исполняется значительно быстрее, но ее отладка значительно труднее. В современном программировании все чаще применяется прием псевдо компиляции, когда программа компилируется в некий промежуточный псевдокод, который потом исполняется в специальном интерпретаторе, называемом средой исполнения. К таким языкам относятся Java, Visual Bask, языки семейства .NET. Фортран Язык Фортран был разработан фирмой IBM. Профессор Дж. Букс и группа американских специалистов в области программирования в 1954 году опубликовали первое сообщение о языке. Дословно название языка FORmula TRANslator — преобразование формул. Фортран в 60-70-е годы являлся одним из самых распространенных языков в мире. Он имеет простую структуру, программа на Фортране записывается в последовательности предложений или операторов (описание некоего преобразования информации) и оформляется по определенным стандартам. Эти стандарты накладывают ограничения, в частности, на форму записи и расположения частей оператора в строке бланка для записи операторов. Программа, записанная на Фортране, представляет собой один или несколько сегментов (подпрограмм) из операторов. Сегмент, управляющий работой всей программы в целом, называется основной программой. Фортран был задуман для использования в сфере научных и инженерно-технических вычислений. Однако на этом языке легко описываются задачи с разветвленной логикой (моделирование производственных процессов, решение игровых ситуаций и т. д.), некоторые экономические задачи и особенно задачи редактирования (составление таблиц, сводок, ведомостей и т. д.). Бейсик Бейсик является сокращением от «Beginner's All-purpose Symbolic Instruction Code» (BASIC) — Многоцелевой Символический Обучающий Код для Начинающих. Бейсик значительно легче в изучении, чем другие языки, с ним легко работать, программы на нем пишутся обычно быстрее, чем на других языках программирования высокого уровня. Долгое время Бейсик был встроен в ПЗУ персональных компьютеров. Бейсик считается деловым языком, снабженным мощными средствами решения специфических задач, которые обычно большинство пользователей решают при помощи небольших компьютеров, а именно: работая с файлами и выводя текстовое и графическое изображение на экране дисплея. Исторически Бейсик обычно реализовался как интерпретатор. Однако сейчас существует множество реализаций Бейсика, использующих методы компиляции и псевдо компиляции. Версия Бейсика от компании Microsoft — Visual Basic — является самым распространенным средством программирования в мире. Его пользуются более 20 миллионов программистов. Си Язык Си — универсальный язык программирования, для которого характерны экономичность выражения, современный поток управления и структуры данных, богатый набор операторов. Язык Си не является языком «очень высокого уровня» и не предназначается для некоторой специальной области применения. Отсутствие ограничений и универсальность языка делают его более удобным и эффективным для многих задач, чем языки, предположительно более мощные. Язык Си, первоначально предназначавшийся для написания операционной системы UNIX на ЭВМ DEC PDP-11, был разработан и реализован на этой системе Деннисом Ричи. Операционная система, компилятор с языка Си и все прикладные программы системы UNIX написаны на Си. Большинство системного программного обеспечения современных компьютеров разрабатывается на Си и его разновидности Си++. Паскаль Язык Паскаль был создан Никлаусом Виртом в конце 60-х годов и назван в честь французского математика Блеза Паскаля. Паскаль по сравнению с другими языками программирования имеет упрощенный синтаксис. Однако Паскаль наиболее близок к идеальному алгоритмическому процедурному языку. Этот язык полностью реализует принципы структурного программирования. Реализация Паскаля под названием Object Pascal и среда программирования Delphi являются одной из самых популярных систем программирования в мире. 20. Структура программы. Переменные, основные операторы языка программирования. Каждая программа на языке программирования высокого уровня должна быть оформлена в соответствии с правилами этого языка. Алгоритмический язык В алгоритмическом языке структура программы имеет следующий вид: алг <имя программы> (<список переменных>) <список аргументов> <список результатов> нач <операторы> кон <имя программы> — идентификатор, однозначно определяющий программу; <список переменных> — список величин, которые обрабатываются программой; <список аргументов> — список величин, которые передаются в программу для обработки; <список результатов> — список величин, которые вычисляются программой; <операторы> — конечная последовательность операторов, реализующих исходный алгоритм и составляющих тело программы. Бейсик <метка> оператор … <метка> оператор <метка> END <метка> — уникальный числовой идентификатор каждой строки, позволяющий операторам перехода изменять ход выполнения операторов. Паскаль Program <имя программы>; <описания> begin <операторы> end <описания> — раздел, в котором описываются модули, используемые программой, константы, переменные, которые используются в программе, описываются пользовательские типы данных, используемые подпрограммы. 21. Условные операторы и операторы цикла. Условный оператор применяется для реализации разветвляющегося алгоритма. В зависимости от значения логической величины, которая может являться результатом операции отношения» выполняется или один или другой оператор (или выполняется переход к той или иной метке в программе).
<Оператор> в алгоритмическом языке и Паскале может быть как простым, так и составным. Составной оператор — это набор простых операторов, ограниченный командами «нс» и «кс» в алгоритмическом языке и begin … end — в Паскале. Разновидностью условного оператора является оператор выбора. Оператор выбора выполняет один из операторов в зависимости от различных значений анализируемой величины:
Циклом называется последовательность операторов, которая выполняется несколько раз, пока выполняется (или ие выполняется) определенное условие или заранее заданное количество раз. Выполняемая в цикле последовательность операторов называется телом цикла. Каждое прохождение цикла называется итерацией. Цикл с предусловием В цикле с предусловием перед началом выполнения каждой итерации проверяется условие. Если оно истинно, то тело цикла выполняется, если ложно — выполнение цикла прерывается и начинают выполняться операторы, расположенные за телом цикла.
В Бейсике циклы реализуются с помощью условного оператора и оператора безусловного перехода. Цикл с послеусловием В цикле с послеусловием после каждой итерации проверяется условие, и в случае истинности выполнение цикла прерывается, иначе выполнение тела цикла повторяется. Вид оператора цикла с послеусловием:
Цикл со счетчиком Цикл со счетчиком используется тогда, когда заранее известно, сколько раз должно быть выполнено тело цикла. В цикле со счетчиком используется переменная — счетчик — которая изменяется в заданном диапазоне.
22. Математическая логика: основные логические операции, таблицы истинности. Слово логика означает совокупность правил, которым подчиняется процесс мышления. Сам термин "логика" происходит от древнегреческого logos, означающего "слово, мысль, понятие, рассуждение, закон". Формальная логика - наука о формах и законах мышления. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика как наука позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления являются понятия, суждения и умозаключения. Понятие - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других. Например, компьютер, человек, ученики. Суждения - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета и которая может быть либо истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение. Вопросительные и побудительные предложения суждениями не являются. Суждения рассматриваются не с точки зрения их смысла и содержания, а только с точки зрения их истинности или ложности. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных объектов. "Дважды два равно четырем" - истинное суждение, а вот "Процессор предназначен для печати" - ложное. Суждения могут быть простыми и сложными. "Весна наступила, и грачи прилетели" - сложное суждение, состоящее из двух простых. Простые суждения (высказывания) выражают связь двух понятий. Сложные - состоят из нескольких простых суждений. Умозаключение - прием мышления, позволяющий на основе одного или нескольких суждений-посылок получить новое суждение (знание или вывод). Примерами умозаключений являются доказательства теорем в геометрии. Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда и умозаключение будет истинным. Иначе можно прийти к ложному умозаключению. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера. Суждения в математической логике называют высказываниями или логическими выражениями. Подобно тому, как для описания действий над переменными был разработан раздел математики алгебра, так и для обработки логических выражений в математической логике была создана алгебра высказываний, или алгебра логики. 7.2. Логические выражения и логические операции Логическое выражение - это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные буквами латинского алфавита. Существуют разные варианты обозначения истинности и ложности переменных:
Связки "НЕ", "И", "ИЛИ" заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение. Логическое отрицание (инверсия). В обыденной речи мы часто пользуемся словом "НЕ", или словами "НЕВЕРНО, ЧТО", когда хотим что-то отрицать. Пусть, например, кто-то сказал: "Тоска зеленая." (Обозначим это высказывание А). Если Вы не согласны, Вы скажете:" Тоска НЕ зеленая." Или:" Неверно, что тоска зеленая." (Ваше высказывание обозначим В). Нетрудно заметить, что значения истинности высказываний А и В находятся в определенной связи: если А истинно, то В ложно, и наоборот. Операция, с помощью которой из высказывания А получается высказывание В, называется логическим отрицанием и само высказывание В называется отрицанием высказывания А и обозначается ¬ А. Таким образом, отрицанием ¬ А некоторого высказывания А называется такое высказывание, которое истинно, когда А ложно, и ложно, когда А истинно. Отрицание высказывания А обозначим ¬А. Определение отрицания может быть записано с помощью так называемой таблицы истинности:
В ней указано, какие значения истинности (Истина, Ложь) принимает отрицание ¬ А в зависимости от значений истинности исходного высказывания А. Логическое умножение (конъюнкция) от латинского conjunctio - союз, связь. Если два высказывания соединены союзом "И", то полученное сложное высказывание обычно считается истинным тогда и только тогда, когда истинны оба составляющие его высказывания. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза "И" сложное высказывание также считается ложным. Например, возьмем два высказывания: "У кота есть хвост" (А), "У зайца есть хвост" (В). Сложное высказывание "У кота есть хвост и у зайца есть хвост" истинно, т.к. истинны оба высказывания А и В. Но если взять другие высказывания: "У кота длинный хвост" (С), "У зайца длинный хвост" (D), то сложное высказывание "У кота длинный хвост и у зайца длинный хвост" будет ложным, т.к. ложно высказывание (D). Таким образом, исходя из обычного смысла союза "И", приходим к определению соответствующей логической операции - конъюнкции. Таким образом, конъюнкцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда истинны оба высказывания А и В. Конъюнкцию высказываний А и В мы обозначим: A & B. Знак & - амперсент - читается как английское "and" (помните Procter & Gamble или Wash & Go?). Часто встречается обозначение А Λ В. Иногда, для краткости, пишут простоАВ. Определение конъюнкции может быть записано в виде таблицы истинности, в которой для каждого из четырех возможных наборов значений исходных высказываний А и В задается соответствующее значение конъюнкции А & В:
Определение конъюнкции двух высказываний естественным образом распространяется на любое конечное число составляющих: конъюнкция А1 & A2 & A3 &...& AN истинна тогда и только тогда, когда истинны все высказывания А1, A2, A3, ...AN (а, следовательно, ложна, когда ложно хотя бы одно из этих высказываний). Логическое сложение (дизъюнкция) от латинского disjunctio - разобщение, различие. Если два высказывания соединены союзом "ИЛИ", то полученное сложное высказывание обычно считается истинным, когда истинно хотя бы одно из составляющих высказываний. Например, возьмем два высказывания: "Мел черный." (А), "Доска черная." (В). Высказывание "Мел черный или доска черная" будет истинным, т.к. одно из исходных высказываний (В) истинно. Таким образом, дизъюнкцией двух высказываний называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний. Дизъюнкцию высказываний А и В мы обозначим символом А V В и будем читать: А или В. Определение дизъюнкции может быть записано в виде таблицы истинности:
Определение дизъюнкции двух высказываний естественным образом распространяется на любое конечное число составляющих: дизъюнкция А1 V А2 V А3 V...V АN истинна тогда и только тогда, когда истинно хотя бы одно из высказываний А1, А2, А3, ..., АN (а следовательно, ложна, когда ложны все эти высказывания). Логическое следование (импликация) от латинского implico - тесно связываю. В наших рассуждениях, особенно в математических доказательствах, мы часто пользуемся сложными высказываниями, образованными с помощью слов "если..., то...". Здесь высказывание, расположенное после слова "если", называется основанием или посылкой, а высказывание, расположенное после слова "то", называется следствием или заключением. Рассмотрим пример: из арифметики. Вам должно быть известно, что утверждение "если каждое слагаемое делится на 3, то и сумма делится на 3" истинно, т.е. из высказывания "каждое слагаемое делится на 3" следует высказывание "сумма делится на 3". Посмотрим, какие наборы значений истинности посылки и заключения возможны, когда истинно все утверждение. Возьмем, например, в качестве слагаемых числа 6 и 9. В этом случае истинны и посылка, и заключение, и все утверждение. Если же взять числа 4 и 5, то посылка будет ложной, а заключение истинным. Для чисел 4 и 7 и посылка и заключение ложны. (Если Вы сомневаетесь в истинности высказывания для последнего случая попробуйте произнести его в сослагательном наклонении: если бы числа 4 и 7 делились бы на 3, то и их сумма делилась бы на 3). Очевидно, что только один случай невозможен: мы не найдем таких двух слагаемых, чтобы каждое из них делилось на 3, а их сумма не делилась на 3, т.е. чтобы посылка была истинной, а заключение ложным. Из истины не может следовать ложь, иначе логика теряет смысл. Высказывание "Если А, то В" с логической точки зрения имеет тот же смысл, что и высказывание "неверно, что А истинно и В ложно". Это означает, что функцию импликации можно заменить комбинацией двух функций (отрицания и конъюнкции). Обычно, когда мы хотим установить ложность высказывания "Если А, то В", мы стараемся показать, что возможен случай, когда А истинно, а В ложно (доказательство "от противного"). Обозначим импликацию символом => и запись "А => В" будем читать: "Из А следует В". Таким образом, импликацией А => В называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно. Запишем это определение в виде таблицы истинности:
Логическое тождество (эквиваленция). Интуитивно можно догадаться, что высказывания эквивалентны (равносильными), когда их значения истинности одинаковы. Например, эквивалентны высказывания: "железо тяжелое" и "пух легкий", так же как и высказывания: "железо легкое" и "пух тяжелый". Обозначим эквиваленцию символом <=> и запись "А <=> В" будем читать "А эквивалентно В", или "А равносильно В", или "А, если и только если В". Таким образом, эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны. Отметим, что высказывание типа "А, если и только если В" можно заменить высказыванием "Если А, то В и, если В, то А" (обдумайте это на досуге и обратите внимание на символ <=>). Следовательно, функцию эквиваленции можно заменить комбинацией функций импликации и конъюнкции. Запишем таблицу истинности для эквиваленции:
Приведем примеры записи сложных высказываний с помощью обозначения логических связок: "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V ¬ A <=> В "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А => В 7.3. Построение таблиц истинности для логических функций Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b). Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки. Предлагается следующий алгоритм построения таблицы истинности. 1. Определить количество наборов входных переменных - всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q=2n , где n - количество входных переменных. Оно определяет количество строк таблицы. 2. Внести в таблицу все наборы входных переменных. 3. Определить количество логических операций и последовательность их выполнения. 4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности. 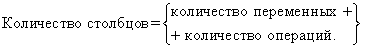 Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных, следует пользоваться одним из предлагаемых ниже способов заполнения таблицы. Способ 1. Каждый набор значений исходных переменных есть код числа в двоичной системе счисления, причем количество разрядов числа равно количеству входных переменных. Первый набор - число 0. Прибавляя к текущему числу каждый раз по 1, получаем очередной набор. Последний набор - максимальное значение двоичного числа для данной длины кода. Например, для функции от трех переменных последовательность наборов состоит из чисел:
Способ 2. Для функции от трех переменных последовательность данных можно получить следующим путем: а) разделить колонку значений первой переменной пополам и заполнить верхнюю половину нулями, нижнюю половину единицами; б) в следующей колонке для второй переменной половинку снова разделить пополам и заполнить группами нулей и единиц; аналогично заполнить вторую половинку; в) так делать до тех пор, пока группы нулей и единиц не будут состоять из одного символа. Способ 3. Воспользоваться известной таблицей истинности для двух аргументов. Добавляя третий аргумент, сначала записать первые 4 строки таблицы, сочетая их со значением третьего аргумента, равным 0, а затем еще раз записать эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк:
Например, построим таблицу истинности для логической функции: Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов Q=23=8. Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов
|