Лекция Управление данными тема 2. Управление данными Тема 2. Терминология реляционной алгебры

• Название: Терминология реляционной алгебры
• Анкор: Лекция Управление данными тема 2
• Дата: 08.09.2021
• Размер: 88.79 Kb.
• Имя файла: Управление данными Тема 2.docx
• Тип: Документы; #230541

Терминология реляционной алгебры

Сильную сторону реляционных баз данных представляет развитая математическая теория, лежащая в их основе – реляционная алгебра.

В основе реляционной модели лежит понятие отношения (от англ. Relation),  которое выражает не взаимосвязь между таблицами-сущностями, а определение самой таблицы как математического отношения доменов.

Домен – это подмножество элементов.

Кортеж представляет собой  упорядоченный конечный набор элементов.

Декартовым произведением доменов D1,D2, …,Dk   D=D1xD2x…xDk,  называется множество всех кортежей длины k (то есть состоящих из k-элементов) по одному из каждого домена Di:    (d1i₁, d2i₂, …, dki_k), где  D1={d11, d12, …, d1n1}, D2= {d21, d22, …, d2n2}, …., Dk = {dk1, dk2, …, dknk}.

Пример. Пусть имеется 3 домена:   D1={A,2}, D2 = {B,C}, D3 = {4,5, D}. Необходимо определить их декартово произведение D1xD2xD3. Поскольку доменов 3, то строим кортежи длиной 3(берем по одному элементу из каждого домена

D = D1xD2xD3 ={(A, B, 4), (A, B, 5), (A, B, D), (A, C, 4), (A, C, 5), (A, C, D),

 (2, B, 4), (2, B, 5), (2, B, D), (2, C, 4), (2, C, 5), (2, C, D)}

Декартово произведение позволяет получить все возможные комбинации элементов исходных множеств.

Определим отношение. Отношение R на множествах D1, D2, …, Dk есть подмножество декартова произведения D1xD2x…xDk, то есть является некоторым подмножеством кортежей арности k (арность – длина кортежа , число элементов нем).

Пример. Имеется 3 домена  D1={A,2}, D2 = {B,C}, D3 = {4,5, D}. Их декартово произведение D = D1xD2xD3 ={(A, B, 4), (A, B, 5), (A, B, D), (A, C, 4), (A, C, 5), (A, C, D), (2, B, 4), (2, B, 5), (2, B, D), (2, C, 4), (2, C, 5), (2, C, D)}.

Можно определить отношение

R1={(A,B.4), (A,C,4)}   D1xD2xD3 или

R2 = {(A,B,4), (A,B,5), (A,B,D), (A,C,4), (2,C,D)}   D1xD2xD3.

Отношение называется нормализованным, если каждая компонента кортежа является простым, атомарным значением, не состоящим из группы значений.

Нормализованное отношение удобно представлять как таблицу, где

• 
  каждая строка есть кортеж, а
  
• 
  каждый столбец соответствует одному и тому же компоненту декартова произведения (одному и тому же домену).
  

Имя таблицы соответствует имени отношения.

Например, отношение R1={(A,B.4), (A,C,4)}   D1xD2xD3 может быть представлено в виде таблицы



Такая таблица обладает следующими свойствами:

• 
  каждая строка есть кортеж из k значений, принадлежащих k столбцам;
  
• 
  порядок столбцов фиксирован;
  
• 
  порядок строк безразличен;
  
• 
  любые две строки различаются хотя бы одним элементом;
  
• 
  строки и столбцы таблицы могут обрабатываться в любой последовательности.
  

Чтобы устранить необходимость фиксированного порядка столбцов в отношении, их именуют.

Столбцы таблицы (отношения) – это атрибуты. Множество значений атрибута есть элементы домена. Список имен атрибутов отношения называется схемой отношения, которая обозначается, как

R(A1, A2, …, Ak),

где Ai, i=1,…,k– атрибуты. По сути здесь представлены имя таблицы (R) и имена столбцов (Ai).

В отношении могут существовать несколько атрибутов, которые однозначно идентифицируют кортеж. Такие атрибуты называются возможными ключами. Один из них выбирается в качестве первичного ключа для обеспечения доступа к кортежам.

Схему реляционной базы можно представить в виде:

R1(A11, A12, …, A1k₁)

R2(A21, A22, …, A2k₂)

………………………

Rm(Am1, Am2, …, Amk_m)

Основные операции реляционной алгебры

Для получения информации из отношений необходим язык манипулирования данными (ЯМД), выполняющий соответствующие операции над отношениями.

Для описания ЯМД используют 3 абстрактных теоретических языка:

• 
  реляционная алгебра,
  
• 
  реляционное исчисление с кортежами и
  
• 
  реляционное исчисление с доменами,
  

По своей выразительности все три языка оказались эквивалентными.

При определении операций реляционной алгебры предполагается, что порядок столбцов в отношении фиксирован, а сами отношения конечны.

Пять операций реляционной алгебры являются основными

• 
  проекция,
  
• 
  объединение,
  
• 
  разность,
  
• 
  декартово произведение и
  
• 
  селекция.
  

Другие часто используемые операции пересечения, соединения и деления можно выразить через пять основных операций. Рассмотрим основные операции реляционной алгебры.

1. Объединение отношений R1 и R2 (R=R1UR2)  - отношение, состоящее из множества всех кортежей, принадлежащих  R1 и R2 за исключением повторяющихся. Эта операция применяется к отношениям одной арности.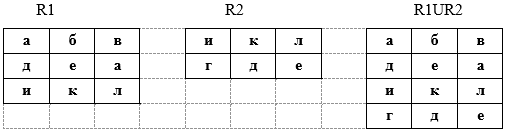



Это можно записать и так

            R1{(а, б, в), (д, е, а), (и, к, л)}

            R2{(и, к, л), (г, д, е)}

            R3 = R1UR2 = {(а, б, в), (д, е, а), (и, к, л), (г, д, е)}

2. Разность отношений R1 и R2 (R=R1-R2) - это отношение, состоящее из множества кортежей, принадлежащих R1 и не принадлежащих R2. Операция применяется к отношениям одной арности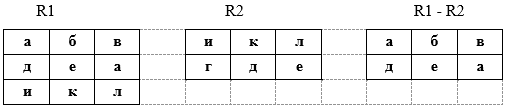



Это можно записать и так

            R1{(а, б, в), (д, е, а), (и, к, л)}

            R2{(и, к, л), (г, д, е)}

            R3 = R1 - R2 = {(а, б, в), (д, е, а)}

3. Декартово произведение отношений R1 и R2 (R=R1xR2) – это множество кортежей арности (k1+k2), причем первые k1 элементов образуют кортеж из отношения R1, а последние k2 элементов образуют кортеж из отношения R2.



Это можно записать и так

            R1{(а, б, в), (д, е, а), (и, к, л)}

            R2{(и, к, л), (г, д, е)}

            R3 = R1xR2 = {(а, б, в, и, к, л), (д, е, а, и, к, л), (и, к, л , и, к, л),

(а, б, в, г, д, е), (д, е, а, г, д, е), (и, к, л , г, д, е)}

4. Проекция отношения R1 на компоненты i1, i2, …, ik  заключается в том, что из отношения R1 выбираются указанные столбцы (i1, i2, …, ik) и компонуются в указанном порядке, записывается как R=π_{i1, i2,…,ik}(R1)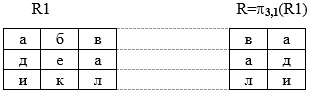



Это можно записать и так

            R1{(а, б, в), (д, е, а), (и, к, л)}

            R = π_3,1(R1) = {(в, а), (a, д), (л, и)}

5. Селекция отношения R1 по формуле F  R=σ_F(R1) - это операция выборки строк (кортежей),  удовлетворяющих формуле F, где F – формула, образованная операндами, являющимися номерами столбцов, и логическими операторами (˄-и, ˅-или, ¬-не), и арифметическими операторами сравнения (<, >, =, ≥, ≠, ≤).



Это можно записать и так

            R1{(а, б, в), (д, е, а), (и, к, л)}

            R=σ_{1=а ˅ 1=д} (R1) = {(а, б, в), (д, е, а)}

Рассмотрим операцию пересечения отношений R1 и R2. Она выражается через известные операции следующим образом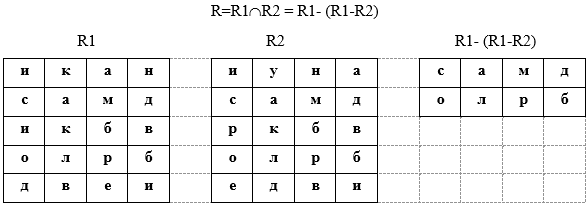

Требования к табличной форме

Поскольку в реляционной модели данные представлены в двумерных таблицах рассмотрим требования к таблицам.

Первое требование– это конечность. Конечное число строк и столбцов таблицы. Работать с большими (бесконечными) таблицами неудобно и довольно редко при этом  оправдываются затраченные усилия

Второе требование касается имени таблицы. Каждая таблица БД должна обладать уникальным именем (имя таблицы, как правило, указывается в единственном числе);

Заголовок таблицы должен обязательно состоять из одной строки, перечня столбцов, причем с уникальными именами. Многоярусные  заголовки не допускаются.



Все многоярусные заголовки заменяются одноярусными путем подбора подходящих заголовков.



Порядок строк и столбцов произвольный, несущественен. Это требование не является строго ограничительным. Если необходимо, можно ввести дополнительный столбец, который будет определять порядок строк. В этом случае от перестановки строк тоже  ничего не изменится.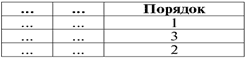



Данные во всех столбцах должны быть одного и того же типа.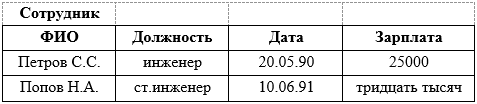



В столбце Зарплата представлены значения двух разных типов данных, что не допустимо.

Значения в ячейках таблицы должны быть атомарны, ячейка не может содержать множественной информации. Значения должны быть простого типа.

Простой тип данных – это такой тип, значения данных которого не содержат составных частей.



В столбцах Имя_реб и Дата_рожд содержится множественная информация. Таблицу следует преобразовать. Строку с множественной информации разбиваем на 2 строки и получаем таблицу с атомарными значениями в ячейках.



Повторение столбцов с одинаковой информацией, например, (Имя_реб1, Дата_р1, Имя_реб2, Дата_р2), не рекомендуется. В этом случае данные лучше выделить в отдельную таблицу.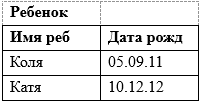

 

Еще одно требование касается наличия строк-дубликатов. В таблице не должно быть строк-дубликатов.  Если же в таблице встречаются повторяющиеся строки, и они необходимы (например, экземпляры книг), то это можно исправить введением дополнительного столбца, отвечающего за количество дубликатов каждой строки (записи).



Рассмотренный абстрактный язык реляционной алгебры служат основой реальных языков манипулирования данных (ЯМД)  реляционных систем.

В общем случае ЯМД выходят за рамки абстрактных языков, так как включают такие команды, как ввод данных, модифицирование данных, удаление данных.