Термодинамические равновесия растворов. Термодинамика растворов Коллигативные свойства растворов. Растворимость
 Скачать 62.31 Kb. Скачать 62.31 Kb.
|
|
Термодинамика растворов Коллигативные свойства растворов. Растворимость Свойства разбавленных растворов, зависящие только от количества нелетучего растворенного вещества в растворе не электролита и не зависящие от его природы, называются коллигативными свойствами. К ним относятся понижение давление пара растворителя над раствором, повышение температуры кипения и понижение температуры замерзания раствора, относительное понижение давления насыщенного пара над раствором, а также осмотическое давление. Понижение температуры замерзания и повышение температуры кипения идеально (предельно разбавленного) раствора нелетучего неэлектролита по сравнению с чистым растворителем описывается законом Рауля: Tзам. = Тfus, 1 – Tfus = K Сm,2 Tкип. =Tv – Тv, 1 = Е Сm,2 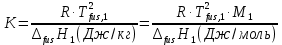  где Сm,2 – моляльность раствора (моль/кг растворителя), K и Е – криоскопическая и эбулиоскопическая постоянные растворителя (Это характеристика исключительно растворителя! Для воды K = 1,86 (кгК)/моль, Е = 0,52 (кгК)/моль), 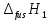 и и 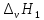 – энтальпии плавления и испарения растворителя, Тfus, 1. и Тv, 1 – температуры плавления и кипения растворителя, M1 – молярная масса растворителя. – энтальпии плавления и испарения растворителя, Тfus, 1. и Тv, 1 – температуры плавления и кипения растворителя, M1 – молярная масса растворителя.Согласно закону Рауля, давление пара растворителя над идеальным (предельно разбавленным) раствором нелетучего неэлектролита пропорционально мольной доле растворителя X1 в растворе:  где p1– давление пара чистого растворителя при данной температуре, X1 – мольная доля растворителя в растворе. Для бинарного раствора закон Рауля можно представить в следующем виде: X1 = 1 – X2, 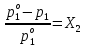 т.е. относительное понижение давления пара растворителя над раствором равно мольной доле X2 растворенного вещества. Если оба компонента раствора летучи, то закон Рауля выполняется для каждого из компонентов:    т.е. общее давление пара над раствором – линейная функция от состава раствора. Осмотическое давление в идеальных (предельно разбавленных) растворах нелетучих неэлектролитов можно рассчитать по уравнению Вант-Гоффа: 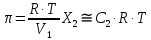 где X2 – мольная доля растворенного вещества, V1– мольный объем растворителя, C2 – молярность раствора. Уравнения, описывающие коллигативные свойства неэлектролитов, можно применить и для описания свойств растворов электролитов, введя изотонический коэффициент Вант-Гоффа i, который связан со степенью диссоциации электролита: AnBm = nAm+ +mBn-
z = n + m – количество ионов, образующихся при диссоциации одной молекулы электролита, = x/Co, i = ni/no = [Co + x(z – 1)]/Co = 1 + ( z – 1) C учетом изотонического коэффициента Вант-Гоффа: Tзам. = Тfus, 1 – Tfus = iK Сm,2 Tкип. =Tv – Тv, 1 = iЕ Сm,2  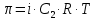 ПРИМЕРЫ Пример 1. Раствор 20 г гемоглобина в 1 л воды имеет осмотическое давление 7,52 10–3 атм при 25oC. Определить молярную массу гемоглобина. Решение. По уравнению Вант-Гоффа 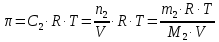  Пример 2. При 30oC давление пара водного раствора сахарозы равно 31,207 мм рт. ст. Давление пара чистой воды при 30oC равно 31,824 мм Hg. Плотность раствора равна 0,б99564 г/см3. Чему равно осмотическое давление этого раствора? Решение. По уравнению Вант-Гоффа 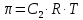 По закону Рауля 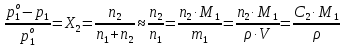 Поделим одно уравнение на другое  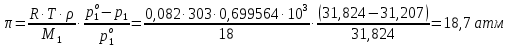 Пример 3. Плазма человеческой крови замерзает при –0,56oC. Каково ее осмотическое давление при 37oC, измеренное с помощью мембраны, проницаемой только для воды? Решение. Tзам. = 0 + 0,56 = 0,56 K, = 1 кг/см3, K = 1,86 (кгК)/моль По уравнению Вант-Гоффа 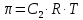 По закону Рауля Tзам. = Тfus, 1 – Tfus = K Сm,2 =  Поделим одно уравнение на другое 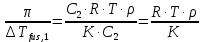 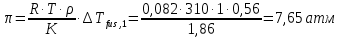 Пример 4. Раствор, содержащий 0,217 г серы и 19,18 г CS2, кипит при 319,304 К. Температура кипения чистого CS2 равна 319,2 К. Эбулиоскопическая постоянная CS2 равна 2,37 (Ккг)/моль. Сколько атомов серы содержится в молекуле серы, растворенной в CS2? Решение: По закону Рауля Tкип. =Tv – Тv, 1 = Е Сm,2 =  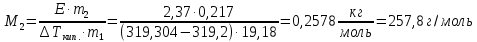 М2 = 32n = 257,8 n = 8 Пример 5. Раствор, содержащий 0,81 г углеводорода H(CH2)nH и 190 г бромистого этила, замерзает при 9,47oC. Температура замерзания бромистого этила 10,00oC, криоскопическая постоянная бромистого этила 12,5 (Ккг)/моль. Рассчитать n. Решение: По закону Рауля Tзам. = Тfus, 1 – Tfus = K Сm,2 = 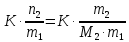  М2 = 12n + 2n + 2 = 14n + 2 = 100,5 n = 7, т.е. C7H16 Пример 6. При растворении 1,4511 г дихлоруксусной кислоты в 56,87 г четыреххлористого углерода точка кипения повышается на 0,518 град. Температура кипения CCl4 76,75oC, энтальпия испарения 46,5 кал/г. Какова кажущаяся молярная масса кислоты? Чем объясняется расхождение с истинной молярной массой? Решение: По закону Рауля Tкип. =Tv – Тv, 1 = Е Сm,2 =  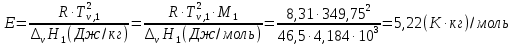 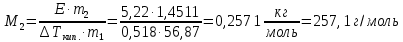 М (CHCl2COOH) = 129 г/моль, т.е. практически вся кислота находится в димерной форме: Mсм = X1M (CHCl2COOH) + X2M((CHCl2COOH)2) = (1 –X2)129 + X2258 = 129 – 129X2 = 257,1, x = 0,993 = 99,3 % Пример 7. Некоторое количество вещества, растворенное в 100 г бензола, понижает точку его замерзания на 1,28oC. То же количество вещества, растворенное в 100 г воды, понижает точку ее замерзания на 1,395oC. Вещество имеет в бензоле нормальную молярную массу, а в воде полностью диссоциировано. На сколько ионов вещество диссоциирует в водном растворе? Криоскопические постоянные для бензола и воды равны 5,12 и 1,86 (Ккг)/моль. Решение: По закону Рауля (Tзам.)’ = Тfus, 1 – (Tfus)’ = K1 Сm,2 (Tзам.)’’ = Тfus, 1 – (Tfus)’’ = iK2 Сm,2  i = 3 Пример 8. Рассчитать состав раствора бензол – толуол, который при нормальном давлении кипит при температуре 100oC, а также состав образующегося пара. Раствор считать идеальным. Давления пара чистых бензола и толуола при 100oC равны 1350 Торр и 556 Торр соответственно. Решение. Мольную долю бензола в растворе находим по закону Рауля: 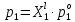 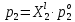 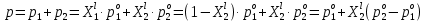 760 = 1350 + (556 – 1350) 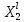 , откуда , откуда 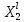 = 0,257 = 0,257Мольная доля толуола в растворе равна 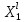 = 1 – = 1 – 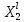 = 0,743 = 0,743По закону Дальтона pi =  p = p = 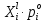 Мольная доля бензола в паре равна 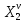 = = 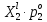 /p= 0,2571350/760 = 0,456 /p= 0,2571350/760 = 0,456Соответственно, мольная доля толуола в паре равна  = 1 – = 1 –  = 0,544. = 0,544.Пример 9. Рассчитать количество водяного пара, необходимое для перегонки 10 кг бензола, если смесь бензола и воды кипит при 69,2оС при нормальном давлении. При этой температуре давление насыщенного пара бензола равно 535 мм Hg, давление насыщенного пара воды равно 225 мм Hg. Решение. Вода и бензол являются практически несмешивающимися жидкостями, поэтому давление насыщенного пара над такой смесью не будет являться функцией от ее состава.  pi =  p = p = 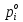  p = p =  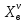 p = p =  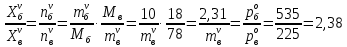 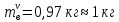 Задачи для самостоятельного решения Задача 1. 68,4 г сахарозы растворено в 1000 г воды. Рассчитать: давление пара осмотическое давление температуру замерзания температуру кипения раствора Давление пара чистой воды при 20oC равно 2314,9 Па, криоскопическая и эбулиоскопическая постоянные воды равны 1,86 и 0,52 (Ккг)/моль соответственно. Задача 2. Некоторое количество вещества, растворенное в 100 г бензола, понижает точку его замерзания на 1,28oC. То же количество вещества, растворенное в 100 г воды, понижает точку ее замерзания на 1,395oC. Вещество имеет в бензоле нормальную молярную массу, а в воде полностью диссоциировано. На сколько ионов вещество диссоциирует в водном растворе? Задача 3. Давления пара чистых C6H5Cl и C6H5Br при 140oC равны 1,237 бар и 0,658 бар. Рассчитать состав раствора C6H5Cl – C6H5Br, который при нормальном давлении кипит при температуре 140oC, а также состав образующегося пара. Каково будет давление пара над раствором, полученным конденсацией образующегося пара? Задача 4. При перегонке нафталина с водяным паром смесь закипает при температуре 95оС. При этой температуре давление насыщенного пара нафталина равно 15,5 м Hg, а давление насыщенного пара воды равно 633,9 мм Hg. Определите в каком весовом соотношении будут переходить в дистиллят нафталин и вода. Растворимость В реальных предельно разбавленных растворах для растворителя выполняется закон Рауля, а для растворенного вещества выполняется закон Генри: p2 = KгX2, где Kг – константа Генри. В идеальных растворах закон Генри совпадает с законом Рауля ( Так как давление газа пропорционально его концентрации в газовой фазе 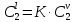 , тогда , тогда 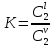 где K – коэффициент пропорциональности называется коэффициентом растворимости Оствальда (s) или коэффициентом адсорбции Бунзена (). Коэффициент растворимости Оствальда (s) или просто растворимость – объем газа, растворяющийся в 1 литре воды при общем давлении 1 атм. Коэффициент адсорбции Бунзена () – объем газа, приведенный к 0оС и 1 атм, растворяющийся в 1 литре воды при парциальном давлении газа 1 атм. Зависимость между коэффициентом растворимости Оствальда и коэффициентом адсорбции Бунзена выражается соотношением: 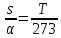 При 0оС s = . Растворимость твердого вещества в идеальном растворе при температуре T описывается уравнением Шредера: 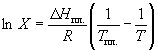 где X – мольная доля растворенного вещества в растворе, Tпл. – температура плавления и Hпл. – энтальпия плавления растворенного вещества. ПРИМЕРЫ Пример 1. Константы Генри для кислорода и азота в воде при 0oC равны 2,54 104 бар и 5,45 104 бар соответственно. Рассчитайте: состав (в %) воздуха, растворенного в воде при 0oC, если воздух над водой состоит из 80% N2 и 20% O2 по объему, а его давление равно 760 мм Hg. понижение температуры замерзания воды, вызванное растворением воздуха, состоящего из 80% N2 и 20% O2 по объему при давлении 760 мм Hg. Решение. По закону Генри: p2 = KгX2, 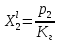 По закону Дальтона pi =  p= p=  pi pi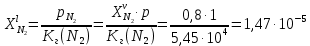 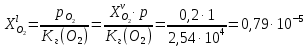  Пусть масса воды 1000 г. 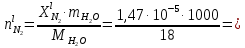 8,210-4 моль 8,210-4 моль 4,410-4 моль 4,410-4 моль =(8,2+4,4)10-4 = 12,610-4 моль =(8,2+4,4)10-4 = 12,610-4 моль  По закону Рауля Tзам. = Тfus, 1 – Tfus = K Сm,2 =  Криоскопическая константа воды равна 1,86 (Ккг)/моль, 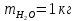 Tзам. =  Пример 2. Рассчитайте коэффициент растворимости Оствальда и коэффициент адсорбции Бунзена NO, если в 1 л воды при 20оС и давлении 600 мм Hg поглощает 52,74 мл оксида азота. Решение. Приведем объем NO к нормальным условиям   объем NO, приведенный к 0оС и 1 атм, поглощаемый 1 л воды при парциальном давлении газа 760 мм Hg  При 0оС  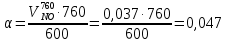 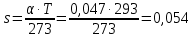 Пример 3. Закрытый сосуд содержит 5 л воды и 1 л NO при нормальном давлении и температуре 0оС. При взбалтывании часть NO растворилась в воде. Вычислите объем NO в растворе, измеренный при 0оС и давлении 760 мм Hg, и конечное давление нерастворившегося остатка NO, если коэффициент растворимости NO равен 0,074. Решение. При растворении NO над раствором устанавливается равновесное давление p. Коэффициент растворимости Оствальда (s) 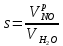  Объем NO, растворившийся в воде при давлении 1 атм:  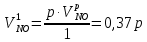 Объем не растворившегося в воде NO при давлении 1 атм: 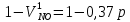 Приведем объем не растворившегося в воде NO к равновесному давлению p:  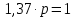 p = 0,73 атм. Пример 4. 10 л Cl2 находится в закрытом сосуде при 20оС и давлении 750 мм Hg. Сколько необходимо литров воды, чтобы парциальное давление Cl2 в сосуде понизилось до 600 мм Hg. Коэффициент растворимости Cl2 при 20оС равен 2,3. Решение. При растворении Cl2 над раствором устанавливается равновесное давление 600 мм Hg. Коэффициент растворимости Оствальда (s)   Объем Cl2, растворившийся в воде при давлении 750 мм Hg:   Объем не растворившегося в воде Cl2 при равновесное давление 600 мм Hg: 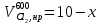 Приведем объем не растворившегося в воде Cl2 к давлению 750 мм Hg: 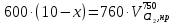 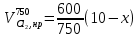 Объем Cl2 при давлении 750 мм Hg составляет 10 л и равен  + + 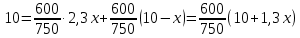 10 + 1,3 x = 12,5 х = 1,92 л Пример 5. Рассчитать растворимость висмута в кадмии при и 200oC. Энтальпия плавления висмута при температуре плавления (273oC) равна 10,5 кДж/моль. Считать, что образуется идеальный раствор и энтальпия плавления не зависит от температуры. Решение. уравнением Шредера: 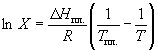  X = 0,7 Задачи для самостоятельного решения Задача 1. Константы Генри для кислорода и азота в воде при 25oC равны 4,40 109 Па и 8,68 109 Па соответственно. Рассчитать состав (в %) воздуха, растворенного в воде при 25oC, если воздух над водой состоит из 80% N2 и 20% O2 по объему, а его давление равно 1 бар. Задача 2. В закрытом сосуде при 20оС и давлении 720 мм Hg содержится 5 л H2S. Сколько необходимо литров воды, чтобы парциальное давление H2S в сосуде понизилось до 600 мм Hg. Коэффициент растворимости H2S при 20оС равен 2,79. Задача 3. Рассчитать растворимость п-дибромбензола в бензоле при 20 и 40oC, считая, что образуется идеальный раствор. Энтальпия плавления п-дибромбензола при температуре его плавления (86.9o C) равна 13.22 кДж/моль. Закон распределения Нернста Отношение концентрации растворенного вещества между двумя несмешивающимися растворителями при данной температуре есть величина постоянная, независящая от абсолютных и относительных количеств всех веществ, участвующих в равновесии (если растворы растворенного вещества в растворителях идеальны и молярная масса растворенного вещества в обеих фазах одинакова, т.е. отсутствует ассоциация или диссоциация): 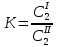 где 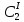 , , 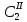 - концентрация растворенного вещества в первом и во втором растворителях при равновесии, K – коэффициент распределения растворенного вещества между первым и вторым растворителем. - концентрация растворенного вещества в первом и во втором растворителях при равновесии, K – коэффициент распределения растворенного вещества между первым и вторым растворителем.Если растворенное вещество диссоциирует или ассоциирует в том или другом растворителе: 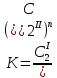 где n = M1/M2, M1 – молярная масса распределяющегося вещества в первом растворителе, M2 – молярная масса растворяющегося вещества во втором растворителе. Закон распределения позволяет получить выражение, позволяющее рассчитать массу (количество) растворенного в исходном растворе вещества после n-ной экстракции: 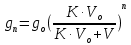 где go – начальное количество вещества, K – коэффициент распределения растворенного вещества между растворителем и экстрагентом, Vo – объем раствора, в котором находится экстрагируемое вещество, V – объем экстрагента, израсходованный на каждое отдельное экстрагирование, n – общее число экстрагировании, gn - количество растворенного в исходном растворе объемом Vo вещества после n-ной экстракции. Примеры Пример 1. Найти концентрацию эфирного раствора янтарной кислоты, находящегося в равновесии с водным раствором, содержащим 0,24 г янтарной кислоты в 100 мл раствора, если при 15оС водный раствор янтарной кислоты, содержащий 0,7 г кислоты в 100 мл раствора, находится в равновесии с эфирным раствором, содержащим 0,13 г кислоты в 100 мл раствора. Янтарная кислота имеет нормальную молярную массу как в воде, так и в эфире. Решение. По закону распределения Нернста коэффициент распределения Нернста янтарной кислоты между водой и эфиром 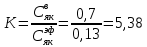 Найдем концентрацию эфирного раствора янтарной кислоты, находящегося в равновесии с водным раствором, содержащим 0,24 г янтарной кислоты в 100 мл раствора:  x = 0,044 г в 100 мл раствора. Пример 2. 1 л амилового спирта содержит 10 г йода. Определите, какое количество йода будет содержаться в воде, если 0,5 л амилового спирта, содержащего йод, взболтать с 2 л воды. Коэффициент распределения йода между амиловым спиртом и водой при 25оС равен 230. Определите, какое количество йода будет содержаться в воде, если 0,5 л амилового спирта, содержащего йод при двукратной экстракции водой порциями по 1 л. Решение. Коэффициент распределения Нернста йода между амиловым спиртом и водой  При однократной экстракции йода водой из раствора йода в амиловом спирте в растворе останется 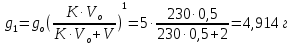 Количество йода, экстрагированного водой g = go – g1 = 5 – 4,914 = 0,086 г 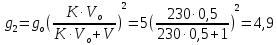 Количество йода, экстрагированного водой g = go – g2 = 5 – 4,9 = 0,1 г Пример 3. 1 л водного раствора содержит 0,3 г йода. Коэффициент распределении йода между амиловым спиртом и водой равен 232,56. Определите, какое количество йода останется в водном растворе, если: Экстракцию проводить однократно 50 мл амилового спирта. Экстракцию производить пятикратно порциями по 10 мл амилового спирта. Решение. Масса растворенного в исходном растворе вещества после n-ной экстракции: 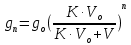 K – коэффициент распределения растворенного вещества между растворителем и экстрагентом. Растворитель – вода, экстрагент – амиловый спирт. Коэффициент распределении йода между водой и амиловым спиртом K = 1/232,56 = 0,0043.  Количество йода, экстрагированного амиловым спиртом g = go – g1 = 0,3 – 0,0235 = 0,2765 г  Количество йода, экстрагированного амиловым спиртом g = go – g1 = 0,3 – 0,000737 = 0,299263 г Задачи для самостоятельного решения Задача 1. Раствор, содержащий 9,86 г фенола в 1 л амилового спирта, находится в равновесии с водным раствором, содержащим 0,616 г фенола в 1 л воды. Сколько грамм фенола экстрагируется из 0,5 л водного раствора фенола, концентрация которого равна 0,3 моль/л, если экстракцию проводить двухкратно порциями по 100 мл амилового спирта. | ||||||||||||||||
