тест по геометрии 8 кл. Тест по геометрии вписанная и описанная окружность. Тест по геометрии Вписанная и описанная окружности
 Скачать 22.81 Kb.
|
|
Тест по геометрии «Вписанная и описанная окружности» Вариант 1. В заданиях № 1 и № 2 вставьте пропущенные слова. 1. Если все стороны многоугольника касаются окружности, то окружность называется _________________________ в многоугольник, а многоугольник _______________________ около этой окружности. 2. Если сумма противоположных углов четырехугольника равна 180о, то ___________________ можно ____________.окружность. В заданиях № 3 – № 8 выберите правильный вариант ответа. 3. Около какого треугольника можно описать окружность? а) прямоугольного; б) тупоугольного; в) остроугольного; г) все варианты верны. 4. Сколько окружностей можно вписать в треугольник: а) Одну; б) Две; в) Три; г) Не в любой треугольник можно вписать окружность. 5. В любом четырехугольнике, описанном около окружности, равны: а) противоположные стороны; б) противоположные углы; в) суммы длин соседних сторон; г) суммы длин противоположных сторон. 6. В треугольник со сторонами 5м, 5м, 8 м вписана окружность с радиусом 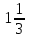 м. Найдите площадь этого треугольника.а) 9 м2; б) 12 м2; в) 18 м2; г) 24 м2. 7. В четырехугольник со сторонами 2 м, 3 м, 7 м вписана окружность. Найдите его четвертую сторону. а) 4 м; б) 5 м; в) 6 м; г) 7 м. 8. Углы вписанного четырехугольника равны 94 о, 57 о, 86 о. Найдите его четвертый угол. а) 86 о; б) 94 о; в) 123 о; г) 132 о. В заданиях № 9 и № 10 необходимо составить рисунок и написать решение. 9. Около прямоугольного треугольника ABC с прямым углом C описана окружность. Найдите радиус этой окружности, если AС = 6 см, ВС = 8 см. 10. В прямоугольный треугольник вписана окружность. Найдите площадь этого треугольника, если точка касания делит гипотенузу на отрезки 4 м и 6 м. Тест по геометрии «Вписанная и описанная окружности» Вариант 2. В заданиях № 1 и № 2 вставьте пропущенные слова. 1. Если все вершины многоугольника лежат на окружности, то окружность называется _____________ около этого многоугольника, а многоугольник – _________________ в эту окружность. 2. Если суммы противоположных сторон выпуклого четырехугольника равны, то ______________ можно ________________.окружность. В заданиях № 3 – № 8 выберите правильный вариант ответа. 3. В какой треугольник можно вписать окружность? а) прямоугольный; б) тупоугольный; в) остроугольный; г) все варианты верны. 4. Сколько окружностей можно описать около треугольника? а) Одну; б) Две; в) Три; г) Не в любой треугольник можно вписать окружность. 5. В любом четырехугольнике, вписанном в окружность: а) суммы противоположных сторон равны; б) сумма противоположных углов равна 180о; в) сумма соседних углов равна 180о; г) противоположные углы равны. 6. Окружность с радиусом  дм вписана в треугольник со сторонами 13 дм, 13 дм, 10 дм. Найдите площадь этого треугольника.а) 18 дм2; б) 36 дм2; в) 60 дм2; г) 68. дм2; 7. Окружность вписана в четырехугольник со сторонами 5 см, 6 см, 7 см. Найдите четвертую сторону этого четырехугольника. а) 4 см; б) 5 см; в) 6 см; г) 7 см. 8. Углы вписанного четырехугольника равны 59 о, 67 о, 121 о. Найдите его четвертый угол. а) 59 о; б) 67 о; в) 103 о; г) 113 о. В заданиях № 9 и № 10 необходимо составить рисунок и написать решение. 9. Около прямоугольного треугольника ABC с прямым углом B описана окружность. Найдите радиус этой окружности, если AB = 9 м, BC = 12 м. 10. В прямоугольный треугольник вписана окружность. Найдите площадь этого треугольника, если точка касания делит гипотенузу на отрезки 5 см и 12 см. Ответы:
|