Вихрь мерсенна. Доклад вихрь мерсенна. Тесты diehard

• Название: Тесты diehard
• Анкор: Вихрь мерсенна
• Дата: 26.02.2023
• Размер: 265.86 Kb.
• Имя файла: Доклад вихрь мерсенна.docx
• Тип: Документы; #956012

Вихрь Мерсе́нна — генератор псевдослучайных чисел (ГПСЧ), разработанный в 1997 году японскими учёными Макото Мацумото и Такудзи Нисимура . Вихрь Мерсенна основывается на свойствах простых чисел Мерсенна  и обеспечивает быструю генерацию высококачественных по критерию случайности псевдослучайных чисел.

В математике простое число Мерсенна-это простое число, которое на единицу меньше степени двойки. То есть это простое число вида Mn = 2n − 1 для некоторого целого числа n. Они названы в честь французского монаха-минима Марина Мерсенна, который изучал их в начале 17 века. Если n − составное число, то и 2n − 1. Поэтому эквивалентное определение простых чисел Мерсенна состоит в том, что они являются простыми числами вида Mp = 2p-1 для некоторого простого p.

Вихрь Мерсенна лишён многих недостатков, присущих другим ГПСЧ, таких как малый период, предсказуемость, легко выявляемые статистические закономерности.

Существуют по меньшей мере два общих варианта алгоритма, различающихся только величиной используемого простого числа Мерсенна, наиболее распространённым из которых является алгоритм MT19937, период которого составляет 2¹⁹⁹³⁷ − 1 (приблизительно 4,3•10⁶⁰⁰¹).

Вихрь Мерсенна является витковым регистром сдвига с обобщённой отдачей

«Вихрь» — это преобразование, которое обеспечивает равномерное распределение генерируемых псевдослучайных чисел в 623. Поэтому функция корреляции между двумя последовательностями выборок в выходной последовательности вихря Мерсенна пренебрежимо мала.

Псевдослучайная последовательность, порождаемая вихрем Мерсенна, имеет очень большой период, равный числу Мерсенна, что более чем достаточно для многих практических приложений.

Выдаваемые вихрем Мерсенна последовательности псевдослучайных чисел успешно проходят статистические тесты DIEHARD, что подтверждает их хорошие статистические свойства.

Генератор не предназначен для получения криптографически стойких случайных последовательностей чисел. Для обеспечения криптостойкости выходную последовательность генератора необходимо подвергнуть обработке одним из криптографических алгоритмов хеширования^[12].

Описание

x будем обозначать w-мерные векторы над полем {\displaystyle F_{2}}F2 = {0,1}, соответствующие машинным словам размера w.

Вихрь Мерсенна генерирует последовательность векторов, которые являются псевдослучайными целыми из диапазона от 0 до 2^w — 1. Путём деления на 2^w — 1 можно также получить псевдослучайное вещественное число из диапазона [0,1].

Алгоритм основан на следующей рекуррентной формуле:

{\displaystyle x_{k+n}:=x_{k+m}\oplus ({x_{k}}^{u}\mid {x_{k+1}}^{l})A,\qquad k=0,1,\ldots \qquad (1)}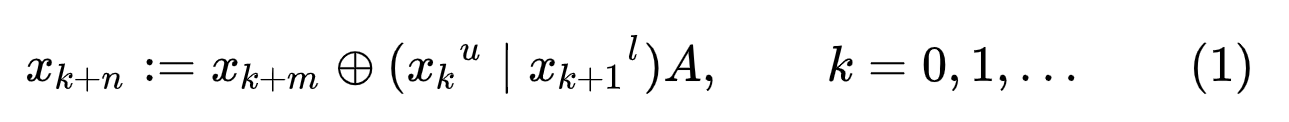

где:

• 
  n - целое, которое обозначает порядок рекуррентности,
  
• 
  m - целое, 1 ≤ m < n,
  
• 
  A - матрица размера w×w, с элементами из {\displaystyle F_{2}}F2,{\displaystyle \mid }
  
• 
  |  — побитовое ИЛИ (OR),
  
• 
  {\displaystyle \oplus } 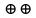 — сложение по модулю два (XOR).
  
• 
  
  

В правой части x_k^u обозначает «старшие w-r бит»

 x_k и x_k+1^l «младшие r бит» x_k+1.

Вектор (x_k^u | x_k+1^l) является конкатенацией старших w-r бит x_k и младших r бит x_k+1. Возьмём (x₀, x₁,…, x_n-1) в качестве начального заполнения. Тогда генератор вычислит x_n по рекуррентному выражению при k= 0.

Полагая k = 1,2, …, генератор вычислит x_n+1, x_n+2,… Форма матрицы A выбрана из расчета скорости выполнения умножения на A:

{\displaystyle A={\begin{pmatrix}0&1&&&&\\0&0&1&&&\\0&\cdots &\cdots &\ddots &&\\&&&&\ddots &\\&&&&&1\\a_{w-1}&a_{w-2}&\cdots &\cdots &\cdots &a_{0}\end{pmatrix}}}

И вычисление xA сводится к побитовым операциям: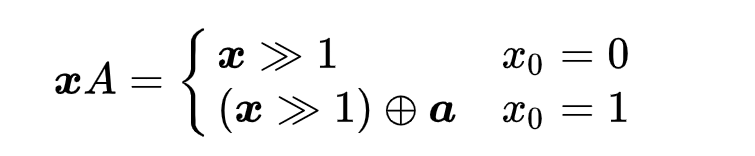



{\displaystyle {\boldsymbol {x}}A={\begin{cases}{\boldsymbol {x}}\gg 1&x_{0}=0\\({\boldsymbol {x}}\gg 1)\oplus {\boldsymbol {a}}&x_{0}=1\end{cases}}}

Где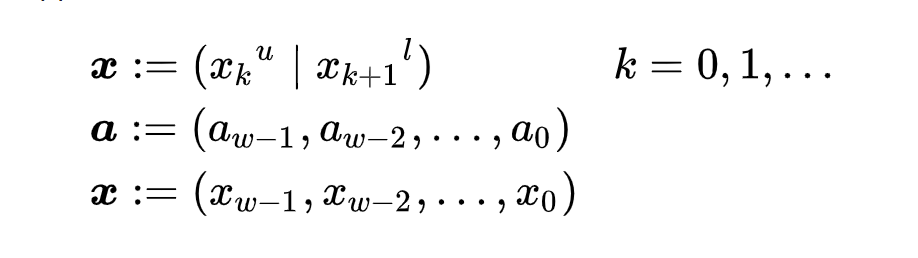



{\displaystyle {\boldsymbol {x}}:=({x_{k}}^{u}\mid {x_{k+1}}^{l})\qquad \qquad k=0,1,\ldots }

Закалка

Необработанные последовательности, генерируемые рекурсией (1), обладают плохим равномерным распределением на больших размерностях. Чтобы это исправить, используется метод закалки (англ. tempering)^[13], на выходе которого получается итоговая псевдослучайная последовательность. Метод заключается в том, что каждое сгенерированное слово умножается справа на специальную обратимую матрицу T размера w × w. Для матрицы T: x → z = x T, выбраны следующие последовательные преобразования: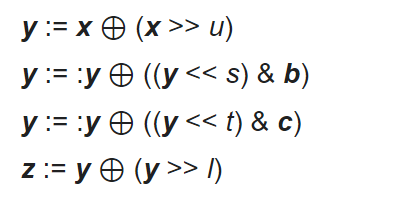



где l, s, t и u — целые, а b и c — специально подобранные битовые маски размера слова, и (x≫u) обозначает побитовую операцию сдвига вправо на u бит.

Алгоритм

Вихрь Мерсенна алгоритмически реализуется двумя основными частями: рекурсивной и закалки.

Рекурсивная часть представляет собой регистр сдвига с линейной обратной связью, в котором все биты в его слове определяются рекурсивно; поток выходных битов определяются также рекурсивно функцией битов состояния.

Если спросит : Регистр сдвига с линейной обратной связью (РСЛОС, англ. linear feedback shift register, LFSR) — сдвиговый^[en] регистр битовых слов, у которого значение входного (вдвигаемого) бита равно линейной булевой функции от значений остальных битов регистра до сдвига.

Регистр сдвига состоит из 624 элементов, и, в общей сложности, из 19937 клеток. Каждый элемент имеет длину 32 бита за исключением первого элемента, который имеет только 1 бит за счет отбрасывания бита.

Процесс генерации начинается с логического умножения на битовую маску, отбрасывающей 31 бита (кроме наиболее значащих).

Следующим шагом выполняется инициализация (x₀, x₁,…, x₆₂₃) любыми беззнаковыми 32-разрядными целыми числами. Следующие шаги включают в себя объединение и переходные состояния.

Пространство состояний имеет 19937 бит (624·32 — 31). Следующее состояние генерируется сдвигом одного слова вертикально вверх и вставкой нового слова в конец. Новое слово вычисляется гаммированием средней части с исключённой^[14]. Выходная последовательность начинается с x₆₂₄, x₆₂₅,…

Алгоритм производится в шесть этапов:

Шаг 0. Предварительно инициализируется значение констант u1, h1, a

u1 ← 10…0   битовая маска старших w-r бит,

h1 ← 01…1   битовая маска младших r бит,

a ← a_w-1a_w-2…a₀  последняя строка матрицы A.

Шаг 1. x[0], x[1],…,x[n-1] ←  начальное заполнение

Шаг 2. Вычисление (x_i^u | x_i+1^l)

y ← (x[i] AND u1) OR (x[(i + 1) mod n] AND h1)

Шаг 3. Вычисляется значение следующего элемента последовательности по

рекуррентному выражению (1)

x[i] ← x[(i + m) mod n] XOR (y>>1) XOR a   если младший бит y = 1

Или

x[i] ← x[(i + m) mod n] XOR (y>>1) XOR 0   если младший бит y = 0

Шаг 4. Вычисление x[i]T

y ← x[i]

y ← y XOR (y>>u)

y ← y XOR ((y<<s) AND b)

y ← y XOR ((y<<t) AND c)

z ← y XOR (y>>l)

вывод z

Шаг 5. i ← (i + 1) mod n

Шаг 6. Перейти к шагу 2.

ДОП ИНФА

{\displaystyle {\boldsymbol {a}}:=({a_{w-1}},{a_{w-2}},\ldots ,{a_{0}})}Последовательность МТ (x_k+n, x_k+n-1,…, x_k+1^u) образует (n × w — r)-массив. Так как r битов отбрасываются, массив называется неполным массивом. Каждый элемент получен из рекуррентного соотношения (1). Смена состояния MT также происходит по линейному соотношению и определяется с помощью линейного преобразования B.

В соответствии с общей теорией линейных рекуррентных последовательностей, каждое значение в (n × w − r)-массиве есть линейная рекуррентная последовательность, соответствующая характеристическому многочлену φ_B(t) преобразования B.

Матрица B имеет размеры (n × w − r) × (n × w − r) и следующую форму:



{\displaystyle {\boldsymbol {x}}:=({x_{w-1}},{x_{w-2}},\ldots ,{x_{0}})}Где I{\displaystyle I_{r}}r — единичная матрица размера r × r.

Для {\displaystyle l=0,1,\ldots }L=0,1 выполняется {\displaystyle (x_{l+n},x_{l+n-1},\ldots ,x_{l+1}):=(x_{l+n-1},x_{l+n-2},\ldots ,x_{l})B}


Характеристический многочлен φ_B(t) преобразования B имеет вид^[13]:

{\displaystyle \Phi _{B}(t)=(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})^{r}+a_{0}(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})^{r-1}+...+a_{r-2}(t^{n}+t^{m})^{w-r}\cdot (t^{n-1}+t^{m-1})+a_{r-1}(t^{n}+t^{m})^{w-r}+a_{r}(t^{n}+t^{m})^{w-r-1}+...+a_{w-2}(t^{n}+t^{m})+a_{w-1}}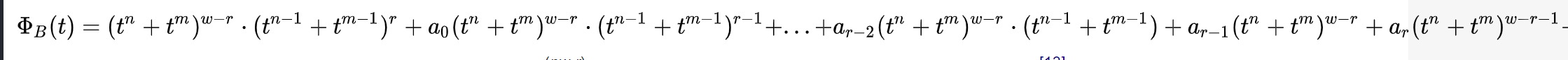

Последовательность достигает максимального периода 2^(nw-r)−1, тогда и только тогда когда φ_B(t) -примитивный

Параметры 32-битного генератора MT

П 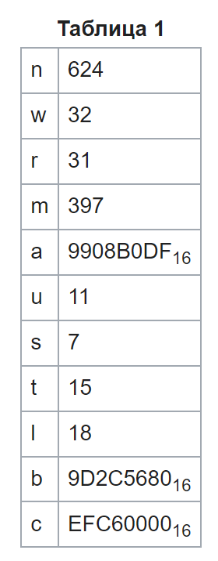араметры MT были тщательно подобраны для достижения упомянутых выше свойств. Параметры n и r выбраны так, что характеристический многочлен примитивный или nw — r равен числу Мерсенна 19937. Обратите внимание, что значение w эквивалентно размеру слова компьютера. В этом случае это 32 бита. В то время как значения n, m, r и w фиксируются, значение последней строки матрицы A выбирается случайным образом.

Параметры закалки (англ. tempering ) подобраны так, что мы можем получить хорошее равномерное распределение.

Все параметры МТ приведены в таблице 1.