Главная страница
Навигация по странице:

  • Скайп

    		•

    Тесты контрольная работа 1. "Основные понятия и свойство алгебраической дроби"


    Скачать 106.54 Kb.
    НазваниеТесты контрольная работа 1. "Основные понятия и свойство алгебраической дроби"
    АнкорKontrolnye-raboty-8-klass-mordkovich.docx
    Дата06.05.2017
    Размер106.54 Kb.
    Формат файлаdocx
    Имя файлаKontrolnye-raboty-8-klass-mordkovich.docx
    ТипТесты
    #7121


    МАТЕМАТИКА В ШКОЛЕ

    УРОКИ, ПРЕЗЕНТАЦИИ, РЕПЕТИТОРЫ, КОНТРОЛЬНЫЕ РАБОТЫ, ЗАДАЧИ, ТЕСТЫ ...


    Контрольная работа №1. "Основные понятия и свойство алгебраической дроби", "Сложение и вычитание алгебраических дробей с одинаковыми и разными знаменателями"
    Вариант I

    1. Найдите значение перемененной х, при котором алгебраическая дробь y + 5 y (y - 5) не имеет смысла?


    2. Найдите значение данного выражения: 6 - 3z 36 - z2 + 5z 36 - z2 при z=-2.

    3. Выполните сложение и вычитание алгебраических дробей:

    алгебраические дроби

    4. Решите задачу:
    Спортсмен проплыл по течению реки 1 км 800 метров за столько же время, сколько 1500 метров по озеру. Какая скорость у спортсмена, если скорость реки 2 км/час.

    5. Задано выражение: выражение
    Докажите, что значение данного выражения положительно при всех допустимых значениях переменной.


    Вариант II

    1. Найдите значение перемененной х, при котором алгебраическая дробь y - 7 y (y + 7) не имеет смысла?


    2. Найдите значение данного выражения: 6 - 7y2 3-y + 6y2 3 - y при z=-3.

    3. Выполните сложение и вычитание алгебраических дробей:

    алгебраические дроби

    4. Катамаран по течению реки проплывает 24 км за такое же время, что и 20 км против течения. Какова скорость реки, если скорость катамарана 22 км/ч.

    5. Задано выражение:
    выражение
    Докажите, что значение данного выражения положительно при всех допустимых значениях переменной.

    Контрольная работа №2. "Умножение и деление алгебраических дробей и возведение их в степень", "Преобразование рациональных выражений", "Степень с отрицательным показателем"


    Вариант I

    1. Выполните умножение и деление дробей: дроби

    2. Вычислите дробь: дроби

    3. Решите уравнение: у + 9y-1 = 18

    4. Упростите выражение: выражение

    5. Решите задачу:
    Из города в село вышел пеший турист. Через 1 час 30 минут вслед за ним вышел велосипедист, скорость которого в 3 раза больше чем у пешехода. Рассчитайте скорость туриста, если в село он пришел в одно время с велосипедистом. Расстояние между городом и селом равно 9 км.


    Вариант II

    1. Выполните умножение и деление дробей: дроби

    2. Вычислите дробь: 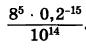дроби

    3. Решите уравнение: 36х - х-1 = 0

    4. Упростите выражение: выражение
    5. Решите задачу.
    Из деревни A в деревню B, расстояние между которыми 100 км, выехал грузовик. Через 40 минут вслед за ним мотоцикл. Скорость мотоцикла в 1,5 раза больше чем скорость грузовика. Какая скорость у грузовика, если в деревню В и грузовик и мотоциклист приехали одновременно?

    Контрольная работа №3. "Рациональные и иррациональные числа", "Понятие квадратного корня", "Функция + √х, её свойства и график", "Свойства квадратных корней"


    Вариант I

    1. Вычислите:   а) 3,4 √64 - 12;   б) √28 - √63 + √112;

    2. Решите заданное уравнение:   6х2 - 7 = 18 - х2

    3. Постройте график функции y = 3 + 2 √x
    - Найдите точку пересечения с прямой x - 2y = 0;
    - Найдите наименьшее и наибольшее значение функции на отрезке [2; 9].

    4. Вычислите:    ( 7 - 4 3 - 2)2

    5. Сократите дробь:   x - 4x + 4 4 - x

    Вариант II

    1. Вычислите:   а) 2,5 √81 + 3;   б) √24 - 4√6 + √54;

    2. Решите заданное уравнение:   2х2 + 4 = -14 - х2.

    3. Постройте график функции y = -2 √x
    - Найдите точку пересечения с прямой 3x - y = 0;
    - Найдите наименьшее и наибольшее значение функции на отрезке [1; 7].

    4. Вычислите:    ( 14 - 6 5 - 3)2

    5. Сократите дробь:   2b - 2b + 1 b - b


    Контрольная работа №4. "Модуль", "Функция y = kx2", "Функция y = k/x"


    Вариант I

    1. Задана функция у = 1,5 х2.
    a) Постройте график функции;
    б) Найдите значение функции, если аргумент равен -3; -1; 4;
    в) Найдите значение аргумента, при котором функция будет равна 3;
    г) Найдите значение аргумента, при котором функция будет <4;
    д) Найдите наибольшее и наименьшее значение функции на отрезке [-4; 0].

    2. Решите уравнение графически: 1,5х2 = х - 5;

    3. Заданы функции: у = f(x) и у = g(x), где f(х) = 4x2; g(x) = x2. Найдите значения аргумента, при котором f(x - 3) = g(x +6).

    4. Вычислите значение P, при котором уравнение не имеет корней: x2 + 1 = p - 3 6


    Вариант II

    1. Задана функция у = 3,5 х2.
    a) Постройте график функции;
    б) Найдите значение функции, если аргумент равен -2; 1; 3;
    в) Найдите значение аргумента, при котором функция будет равна 7;
    г) Найдите значение аргумента, при котором функция будет < 2;
    д) Найдите наибольшее и наименьшее значение функции на отрезке [-2; 2].

    2. Решите уравнение графически: -1,5х2 = х - 3;

    3. Заданы функции: у = f(x) и у = g(x), где f(х) = 4/х; g(x) = 1/2. Найдите значения аргумента, при котором f(x + 1) = g(x2 - 1).

    4. Вычислите значение P, при котором уравнение не имеет корней: x2 + 3 = 3p + 2 4


    Контрольная работа №5. "График функции f(x + l)", "График функции f(x) + m", "График функции f(x + l) + m", "Функция y = ax2 + bx + c", "Графическое решение квадратных уравнений"


    Вариант I

    1. Задана функция y = √x - 4. Постройте его график и укажите множество значений функции.
    2. Задана функция y = x2 + 4x + 3. Постройте его график и с помощью графика найдите:
    а) промежутки, в которых график возрастает;
    б) промежутки в которых график убывает;
    в) наибольшее значение функции;
    г) при каких значениях x y<0.
    3. Решите графически заданное уравнение y = x2 - 2x - 8.
    4. Задана прямая х=-1. Известно, что она является осью симметрии для параболы y=px2 - (p + 12)x - 15.
    5. Решите графически систему уравнений: система уравнений


    Вариант II

    1. Задана функция y = √x + 5. Постройте его график и укажите множество значений функции.
    2. Задана функция y = -x2 + 2x + 3. Постройте его график и с помощью графика найдите:
    а) промежутки, в которых график возрастает;
    б) промежутки в которых график убывает;
    в) наибольшее значение функции;
    г) при каких значениях x y<0.
    3. Решите графически заданное уравнение y = -x2 - 3x + 4 =0.
    4. Задана прямая х=-1. Известно, что она является осью симметрии для параболы y=px2 - (p + 12)x - 15.
    5. Решите графически систему уравнений: система уравнений


    Контрольная работа №6. "Формулы корней квадратных уравнений", "Рациональные уравнения"


    Вариант I

    1. Определите количество корней у заданных уравнений:
    а)2x2 + х + 5 = 0;      б)x2 -11x - 42 = 0.

    2. Решите заданные уравнения:
    а)x2 + 7х - 60 = 0;      б)-x2 -3x - 6 = 0.
    3. Решите уравнение: уравнение
    4. Катет прямоугольного треугольника на 6 см меньше другого каткта. Чему равны катеты треугольника, если площадь треугольника равна 56 см2.
    5. Вычислите значение p уравнения, если уравнение x2 p x + 2 = 0 имеет только один корень?


    Вариант II

    1. Определите количество корней у заданных уравнений:
    а)-x2 + 3х - 7 = 0;      б)0,5x2 -x - 8 = 0.

    2. Решите заданные уравнения:
    а)-2x2 -5х - 2 = 0;      б)-3x2 - 10x - 3 = 0.

    3. Решите уравнение: уравнение
    4. У прямоугольника одна сторона меньше другой на 4 см. Найдите стороны прямоугольника, если его диагональ равна 18 см.
    5. Вычислите значение p уравнения, если уравнение (p + 2)x2 (p + 2)x + 2 = 0 имеет только один корень?


    Контрольная работа №7. "Рациональные уравнения как математическая модель", "Частные случаи корней квадратного уравнения", "Теорема Виета"


    Вариант I

    1. Решите уравнения:
    а)2x2 + х + 5 = 0;      б)x2 - 11x - 42 = 0.

    2. Сократите дробь: x 2 - 64 x 2 - 11 x + 24

    3. Отношение у корней данного квадратного уравнения x2 + 2x + m равно 6. Найдите корни уравнения и значение m.

    4. Решите задачу:
    Автобус проехал 60 км по асфальтированной дороге и 32 км по грунтовой дороге. На всю дорогу он затратил 60 минут. Найдите скорость автобуса на каждом участке, если на шоссе он двигался ан 20 км/ч быстрее.

    5. Упростите выражение: ( x x + 2 + 4 x 2 - 3х - 2 x - 5 ) : x - 7 x 2 + 2x

    Вариант II

    1. Решите уравнения:
    а)7x2 + 4х + 5 = 0;      б)x2 - 106x + 693 = 0.

    2. Сократите дробь: 3x 2 - 25x - 18 x 2 - 5 x - 36

    3. Вычислите значение параметра q, при котором один из корней уравнения x2 + qx + 48 = 0 в 3 раза больше другого .

    4. Решите задачу:
    Расстояние между двумя городами А и Б равно 240 км. Навстречу друг другу одновременно выехали 2 автомашины "Газ" и "Урал". Скорость автомобиля "Газ"больше скорости автомобиля "Урал" на 20 км/час. Поэтому "Газ" проехал свой путь от А до Б на 1 час быстрее, чем "Урал" от пункта Б до А. Найдите скорости автомобилей.

    5. Упростите выражение: x 2 - 9 10 + 3x * ( 2 x - 4 - 4х x 2 - x - 12 - 1 x + 3 )


    Контрольная работа №8. "Свойства числовых неравенств", "Монотонность функций", "Линейные и квадратные неравенства"


    Вариант I

    1. Решите неравенства:
    а)x2 + 7х - 8 > 0;      б)3x2 - 4x - 1 < 0.

    2. Решите уравнения: а) 5х - 18 2,5 √х - 8 =0; б) √33 - 8 х = х;

    3. При каких значениях параметра m уравнение x2- 2 (m + 3)x + 16 имеет хотя бы один корень?

    4. Найдите область определения для выражения √2 - 5х

    Вариант II

    1. Решите неравенства:
    а)12x + 8 < 3( 4x -2);      б)x2 - 11x - 24 < 0.

    2. Решите уравнения: а) 3x - 2√х - 8 =0; б) √2х + 15 = х;

    3. При каких значениях параметра m уравнение mx2- 2mx + 9 имеет два корня?

    4. Найдите область определения для выражения 1 / √4x +3


    Скайп: mathematics-tests

    Тел: +7 906 384 18 43
    Сайт: http://www.mathematics-tests.com

    Эл. адрес: admin@ mathematics-tests.com

    написать администратору сайта