Тестовые вопросы
по Дискретной математике
1Тип - дистрибутивный вопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 5}, B={2,4,5,6}, C={1,3,5,6}.
Найти  (Указать правильные варианты ответов). (Указать правильные варианты ответов).
{x| x < 7,  } }
{1,2,2,3,4,4,5,6}
{1,2,3,4,5,6}
{1,3}
{3,4,2,5,1,6}
2Тип - дистрибутивныйвопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 4}, B={2,4,5,7}, C={1,2,5,6}.
Найти  (Указать правильные варианты ответов). (Указать правильные варианты ответов).
{1,2,3,5,6}
{1,1,2,2,3,5,6}
{x| x < 7}
{3,2,6,1,7}
{1,2}
3Тип - дистрибутивный вопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x > 4}, B={3,5,7}, C={1,2,4,6}.
Найти  (Указать правильные варианты ответов). (Указать правильные варианты ответов).
U
0{3,5,7}

{3,5,7,1,2,4,6}
<variant>{1,2,3,4,5,6,7}
4Тип - дистрибутивный вопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 5}, B={2,4,5,6}, C={1,3,5,6}.
Найти 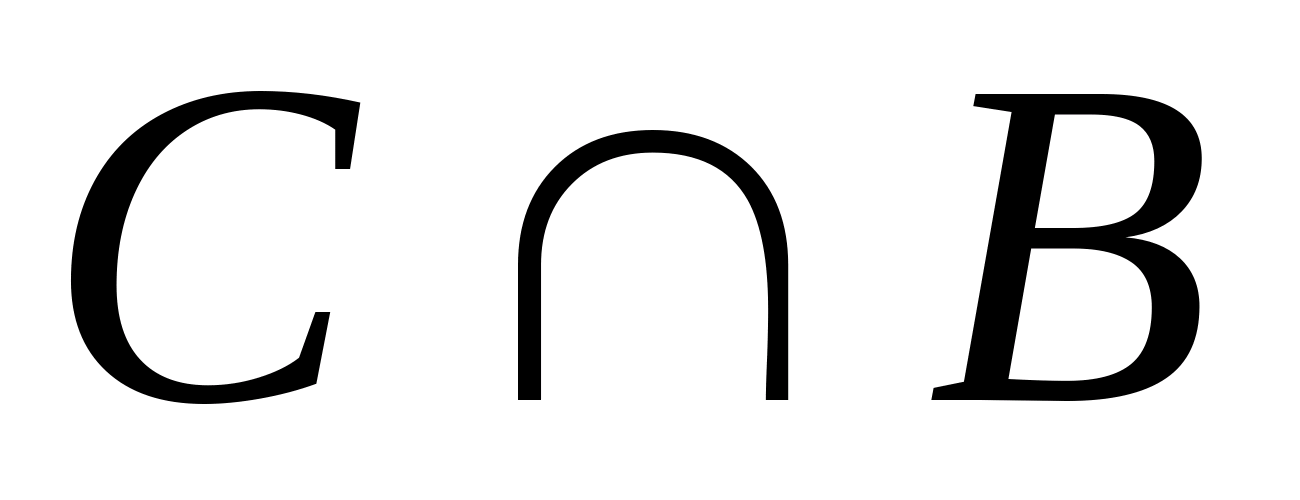 (Указать правильные варианты ответов). (Указать правильные варианты ответов).
{5,6}
{1,2,3,4,5,5,6,6}
{7,5}
{1,2,3,4,5,6}
{x| x < 7}
5Тип - дистрибутивный вопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 4}, B={2,4,5,7}, C={1,2,5,6}. Найти 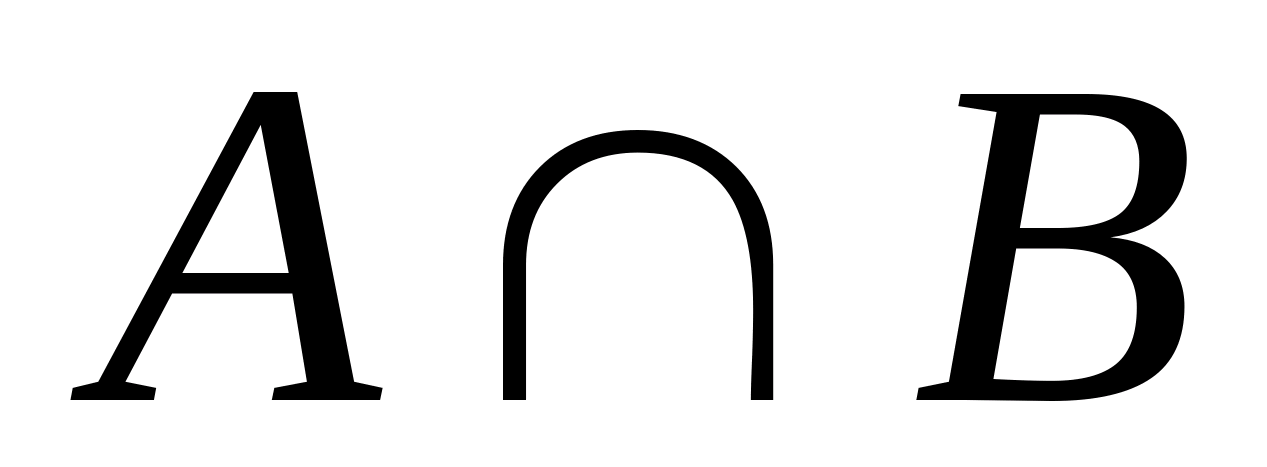 (Указать правильные варианты ответов). (Указать правильные варианты ответов).
<variant>{2}
<variant>{1,2,3,4,5,7}
<variant>{1,2,2,3,4,5,7}
<variant>{5,6}
<variant>{x| x=3}
6Тип - дистрибутивный вопрос.
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x > 4}, B={3,5,7}, C={1,2,4,6}.
Найти 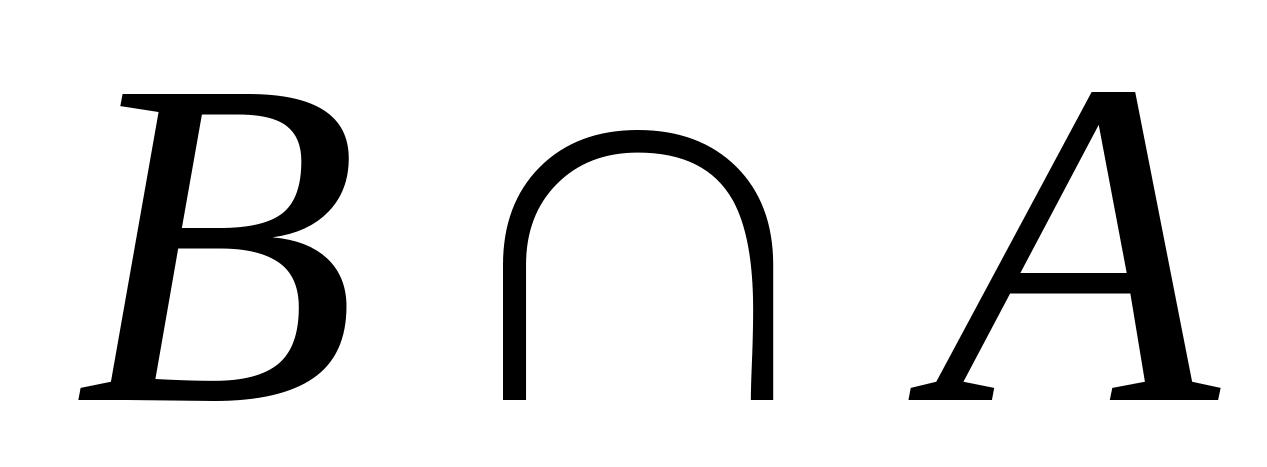 (Указать правильные варианты ответов). (Указать правильные варианты ответов).
{5,7}
{8,5}
{3,5,6,7}
{5,7,5,7}
{x| 2 < x < 8}
7Тип - дистрибутивный вопрос
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 5}, B={2,4,5,6}, C={1,3,5,6}.
Найти декартово (прямое) произведение  , где , где 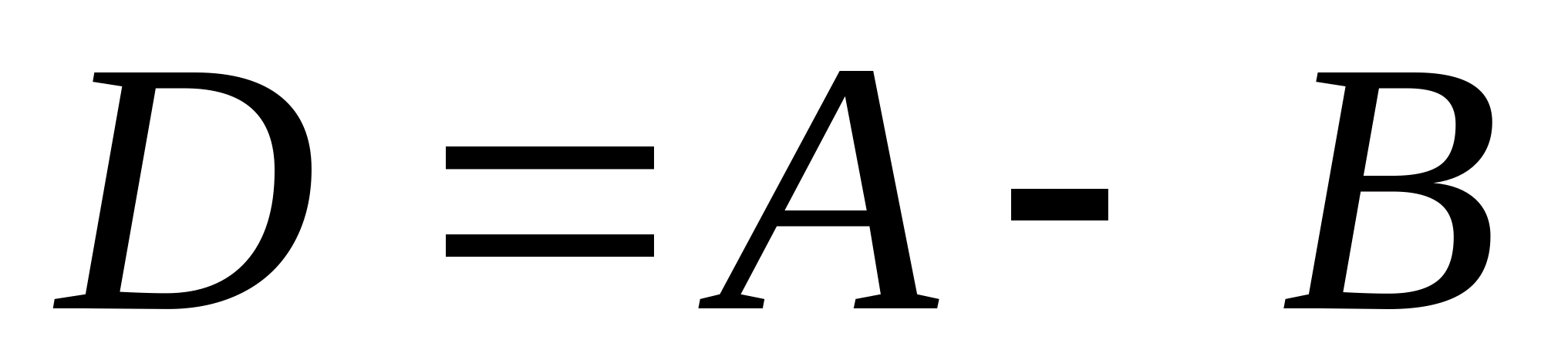 (Указать правильные варианты ответов). (Указать правильные варианты ответов).
{(1,1), (3,1), (1,3), (3,3), (1,5), (3,5), (1,6), (3,6)}
{1,3,5,6}
{(1,1), (1,3), (3,3), (1,5), (3,5), (1,6), (3,6)}
{ (1,3), (1,5), (3,5), (1,6), (3,6)}
{ (3,3), (1,5), (3,5), (1,6), (3,6), (1,1), (3,1), (2,3)}
8Объединением двух множеств А и В считает множество С элементы которых состоит
<variant>из всех элементов которые входят обоим множествам
<variant>из всех элементов которые не входят обоим множествам
<variant>из всех элементов которые не входят к множеству А
<variant>одновременно принадлежащих к обоим множествам
<variant>предельных элементов из множеств А и В
9Пересечением двух множеств А и В считает множество С элементы которых состоят
<variant>одновременно принадлежащих к обоим множествам
<variant>из всех элементов которые входят обоим множествам
<variant>из всех элементов которые не входят обоим множествам
<variant>из всех элементов которые не входят к множеству А
<variant>предельных элементов из множеств А и В
10Разностью двух множеств А и В считает множество С элементы которых состоит
<variant>из элементов множества А которые не входят одновременно к множеству В
<variant>из элементов множества В которые не входят одновременно к множеству А
<variant>из всех элементов которые не входят обоим множествам
<variant>из всех элементов которые не входят к множеству А
<variant>предельных элементов из множеств А и В
11 Коммутативность это
АᴠВ=ВᴠА
(АᴠВ) ᴠС=Аᴠ(ВᴠС)
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
АᴠА=А
<variant>Аᴠ(АᴧВ)=А
12Ассоциативность это
(АᴠВ) ᴠС=Аᴠ(ВᴠС)
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
АᴠА=А
Аᴠ(АᴧВ)=А
АᴠВ=ВᴠА
13Дистрибутивность это
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
АᴠА=А
Аᴠ(АᴧВ)=А
АᴠВ=ВᴠА
(АᴠВ) ᴠС=Аᴠ(ВᴠС)
14Идемпотентность это
АᴠА=А
Аᴠ(АᴧВ)=А
АᴠВ=ВᴠА
(АᴠВ) ᴠС=Аᴠ(ВᴠС)
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
Закон поглощения это
Аᴠ(АᴧВ)=А
АᴠВ=ВᴠА
(АᴠВ) ᴠС=Аᴠ(ВᴠС)
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
АᴠА=А
12 Закон де Моргана это
АᴠВ=АᴧВ
АᴠВ=ВᴠА
v(АᴠВ) ᴠС=Аᴠ(ВᴠС)
Аᴠ(ВᴧС)=(АᴠВ)ᴧС
АᴠА=А
13Бинарным отношением называется множество
<variant>Упорядоченных пар
<variant>Отрицательных элементов
<variant>Положительных элементов
<variant>Двойственных чисел
<variant>Вершин и ребер
14Закон размещения описывает задачу
<variant>расположения
<variant>разделения
<variant>оптимального плана
<variant>логистики
<variant>отчуждения
15 Задача о маршрутах описывает задачу
<variant>оптимального плана
<variant>расположения
<variant>разделения
<variant>логистики
<variant>отчуждения
16 Формула бином Ньютона





17Чему равен А\(А\В)=
АᴧВ
АᴠВ
А/В
<variant>А*В/В
<variant>В-А
18Чему равен (А\В)\С
А\(ВᴠС)
АᴧВᴠС
В*А
<variant>А+В
<variant>А*С/В
19Граф это элемент состоящий из
<variant>Вершин и ребер
<variant>Прямых
<variant>Точек и ребер
<variant>Замков
<variant>Мостов и вершин
20Прямое произведение множества А хВ
<variant>Множество всех пар
<variant>Множество всех вершин
<variant>Множество всех ребер
<variant>Множество всех скобок
<variant>Множество графов
21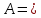 {1,2} B={2,3} тогда А х В= {1,2} B={2,3} тогда А х В=
{(1,2),(1,3),(2,2),(2,3)}
{(1,1),(1,3),(2,2),(2,3)}
{(1,2),(1),(2,2),(2,3)}
{(1,2),(1,3),(2,2),(2,2)}
{(1,2),(2,2),(2,3)}
22Булевы функции принимает .......значения
<variant>2
3
1
4
0
23Логическое умножение это ........
Конъюнкция
Дизъюнкция
Импликация
Инверсия
Обнуление
24Дизъюнкция это .......
<variant>Логическое сложение
<variant>Логическое умножение
<variant>Отрицание
<variant>Отражение
<variant>Логическое деление
25Диаграмма Вейча отражает ......
<variant>Таблицу истинности
<variant>графа
<variant>долготу операции
<variant>Высоту ребра
<variant>Таблицу лжи
26Сложение по модулю 2 . Значение 1+1 будет равен
0
1
10
01
11
27 Конъюнкция. Значение 1&1 будет равен
1
0
10
01
11
28 Стрелка Пирса. Значение 00 будет равен
1
0
10
01
11
29Эквивалентность. Значение 1≡1 будет равен
1
0
10
01
11
30Импликация. Значение 1→0 будет равен
<variant>0
<variant>10
<variant>01
<variant>00
<variant>1
11
31Штрих Шеффера. Значение 1|1 равен
0
10
01
00
11
32 Стрелка Пирса. Значение 01 будет равен
0
1
10
01
11
33Эквивалентность. Значение 1≡0 будет равен
0
1
10
01
11
34Импликация. Значение 0→1 будет равен
1
10
01
00
11
35Штрих Шеффера. Значение 0|0 равен
1
10
01
00
0
36 Свойства нуля. Это АᴠØ=
A
0
1
Ø
<variant>AA
37Множество- это совокупность .......... элементов.
<variant>однотипных
<variant>разнотипных
<variant>острых
<variant>прямых
<variant>цветных
38 Множество Z+ это множестово
<variant>всех натуральных чисел (включая 0).
<variant>всех целых чисел
<variant>всех действительных чисел
<variant>всех комплексных чисел
<variant>всех логических чисел
39 Множество Z это множестово
<variant>всех целых чисел
<variant>всех действительных чисел
<variant>всех комплексных чисел
<variant>всех логических чисел
<variant>всех натуральных чисел (включая 0).
40Множество R это множестово
<variant>всех действительных чисел
<variant>всех комплексных чисел
<variant>всех логических чисел
<variant>всех натуральных чисел (включая 0).
<variant>всех целых чисел
41 Множество C это множество
<variant>всех комплексных чисел.
<variant>всех логических чисел
<variant>всех натуральных чисел (включая 0).
<variant>всех действительных чисел
<variant>всех целых чисел
42Мощностью множества M называется .....
<variant>число его элементов
<variant>несопоставимость его элементов
<variant>число требований к его элементам
<variant>число его положительных элементов
<variant>число его максимальных элементов
43 При n = 2 можно получать таблицу истинности, в которой .....значений
16
32
4
8
64
44Высказывание –это .......
<variant>некое утверждение о котором можно говорить что оно истинно или ложно
<variant> аксиома
<variant>Теорема которую надо доказать
<variant>некое утверждение о котором можно говорить что оно спорно
<variant>некое утверждение о котором можно говорить что оно необходимо
45Х=1 Y=1 тогда ХvY=
1
0
11
00
10
46 Х=1 Y=0 тогда ХᴧY=
0
1
11
00
10
47Х=1 Y=0 тогда Х→ Y=
0
1
11
00
10
48Х=0 Y=0 тогда ХY=
1
0
11
00
10
49 Две функции называются ...........если они принимают одинаковые значения на любом наборе
<variant>равносильными
<variant>равнозначным
<variant>положительным
<variant>отрицательным
<variant>нивелирущим
50 Если х ᴠ 1 то
1
0
Х
Х1
1х
51 Если х &1 то
1
0
х
х1
1х
52 Если x v x то
х
1
0
Х1
1х
53Если х ᴠ 0 то
х
0
1
10
х1
54Если x & 0 то
0
1
х
10
11
55Если x&x то
х
0
1
1х
хх
56Пара (V, E), где V – множество вершин, E – множество инцидентных им ребер называется
графом
маршрутом
цепью
<variant>контуром
<variant>прямой
57Чередующаяся последовательность х1,u1,х2u2…..xk,xkвершин и ребер графа, такая, что ui=xixi+1i=1,k называется
маршрутом
графом
цепью
<variant>контуром
<variant>прямой
58Маршрут называется цепью, если все его ребра
<variant> Различны
<variant>Одинаковы
<variant>Железные
<variant>Крепки
<variant>Круглые
59 Маршрут называется простой цепью, если все его вершины
<variant> Различны
<variant>Одинаковы
<variant>Железные
<variant>Крепки
<variant>Круглые
60Маршрут называется циклическим если
x1=xk+1
x1=xk+2
x1=xk-1
x1=x+1
<variant>x1=xk
61Граф называется связанным если любые две его несовпадающие вершины соединены
Маршрутом
Цепью
Вершиной
<variant>Ребром
<variant>орграфом
62Если ребра графа имеют направление то его называют
Орграфом
Маршрутом
Цепью
<variant>Вершиной
<variant>Ребром
63Алгоритм Дейкстры используется для нахождения
<variant>Кратчайших путей
<variant>Длинных путей
<variant>Прямых путей
<variant>Связанных путей
<variant>Внутренных путей
64 Метод динамического программирования используется для нахождения
<variant>Кратчайших путей
<variant>Длинных путей
<variant>Прямых путей
<variant>Связанных путей
<variant>Внутренных путей
65 Задачу о графах поставил
Эйлер
Ньютон
Паскаль
<variant>Морган
<variant>Данциг
66Транспортная задача- это задача которая
<variant> определяет оптимальный план поставки однородного груза из пунктов производства в пункты потребления
<variant>определяет затратный план поставки однородного груза из пунктов производства в пункты потребления
<variant>используют максимальное количество маршрутов доставки грузов
<variant>используют минимальное количество маршрутов доставки грузов
<variant>реализуют транспортных средств
67Транспортная задача.Аі- это
<variant>количество груза в і-пункте поставки
<variant>количество оптимального маршрутов
<variant>тариф і-го маршрута
<variant>количество ортимальных маршрутов
<variant>оценка і-го потенциала
68Транспортная задача. Вj- это
<variant>необходимое количество груза в j - пункте потребления
<variant>количество оптимального маршрутов
<variant>тариф j -го маршрута
<variant>количество ортимальных маршрутов
<variant>оценка j -го потенциала
69Транспортная задача. Хіj- это
<variant>количество груза которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество маршрута которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество тарифов которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество времени которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество информации которое поставляется из і-го пункта поставки в j-й пункт потребления
70Транспортная задача. Сіj- это
<variant>тариф указывающий на доставку единицы однородного груза из і-го пункта в j пункт потребления
<variant>количество груза которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество маршрута которое поставляется из і-го пункта поставки в j-й пункт потребленияаравы
<variant>количество времени которое поставляется из і-го пункта поставки в j-й пункт потребления
<variant>количество информации которое поставляется из і-го пункта поставки в j-й пункт потребления
71 Транспортная задача. Целевая функция будет иметь вид:
F(x)min=
F(x)max=
F(x)max=
F(x)max=
F(x)min=
72 =bjj=1,n означает что =bjj=1,n означает что
<variant>Все грузы из пункта поставки должны быть отгружены
<variant>Все потребности в грузах в пунктах должны быть удовлетворены
<variant>Транспортная задача имеет закрытого типа
<variant>Транспортная задача имеет открытого типа
<variant>Транспортная задача имеет самый оптимальный план
73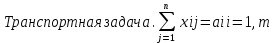 означает что означает что
<variant>Все потребности в грузах в пунктах должны быть удовлетворены
<variant>Транспортная задача имеет закрытого типа
<variant>Транспортная задача имеет открытого типа
<variant>Транспортная задача имеет самый оптимальный план
<variant>Все грузы из пункта поставки должны быть отгружены
74 означает что означает что
<variant>Модель транспортной задачи закрыта
<variant>Транспортная задача имеет открытого типа
<variant>Транспортная задача имеет самый оптимальный план
<variant>Все грузы из пункта поставки должны быть отгружены
<variant>Модель транспортной задачи открыта
75 означает что означает что
<variant>Модель транспортной задачи открыта
<variant>Транспортная задача имеет самый оптимальный план
<variant>Все грузы из пункта поставки должны быть отгружены
<variant>Модель транспортной задачи закрыта
<variant>Транспортная задача в принципе не решается
76Транспортная задача. Для решения ТЗ используетсяметод
<variant>потенциалов
<variant>напряжений
<variant>Эйлера
<variant>стыковок
<variant>правдоподобия
77Транспортная задача. Построение системы потенциалов осуществляется на основе уравнения
cij=ui+vj
cij=ui-vj
cij=ui/vj
cij=ui*vj
cij=(ui+vj)/2
78Транспортная задача. Начальный план перевозок строится наметоде
<variant>северо-западного угла
<variant>юго-восточного угла
<variant>северо-восточного угла
<variant>юго-западного угла
<variant>диагоналя
80Транспортная задача. Оптимальность плана перевозки определяется по формуле:
Wij=cij-(ui+vj)
Wij=cij+(ui+vj)
Wij=cij-(ui-vj)
Wij=cij*(ui+vj)
Wij=cij-(ui*vj)
81Транспортная задача. Улучшение плана осуществляется через
<variant> замкнутый контур
<variant>открытый контур
диагонали
петлю
ребро
82Транспортная задача. Количество оптимальных маршрутов определяется по формуле
k=m+n-1
k=m+n
m=k+m+1
k=m-n-1
<variant>k=n
83Транспортная задача. Если количество маршрутов будет меньше чем надо то используются
<variant> фиктивный маршрут с нулевыми тарифами
<variant>фиктивный маршрут с единичными тарифами
<variant>замкнутый контур
<variant>открытый контур
<variant>диагональ
84Транспортная задача.Метод наименьших стоимостей используется для
<variant>построения первого опорного плана
<variant>построения второго опорного плана
<variant>построения последнего опорного плана
<variant>нахождения кратчайших путей
<variant>определения количества маршрута
85Транспортная задача. Для решения ТЗ в ЕХСЕL используется программа
<variant>Поиск решения
<variant>Анализа данных
<variant>Поиск путей
<variant>Сравнения данных
<variant>Определения тренда
86Транспортная задача.ТЗ является задачей
<variant>Линейного программирования
<variant>Нелинейного программирования
<variant>Динамического программирования
<variant>Факторного анализа
<variant>Дисперсионного анализа
87Сетевое планирование- это
<variant> метод планирования работ операции в которых не повторяется
<variant>метод планирования работ операции в которых повторяется
<variant>метод построения сетевого маркетинга
<variant>метод планирования проекта
<variant>метод построения кодов
88Событие это
<variant> факт окончания всех входящих в сеть работ
<variant>интерпретация окончания всех входящих в сеть работ
<variant>факт которого надо фиксировать
<variant>факт окончания всех невходящих в сеть работ
<variant>факт начала всех невходящих в сеть работ
89На сетевом графе события изображаются
<variant> в виде вершин графа
<variant>прямой
<variant>точки
<variant> в виде ребра графа
<variant>диагонали графа
90Самый продолжительный путь сетевого графика от исходного события к завершающему называется
<variant>критическим
<variant>минимальным
<variant>оптимальным
<variant>максимальным
<variant>неправильным
91Комбинаторика является разделом дискретной математики, ориентированным на решение задач
<variant>выбора и расположения элементов
<variant>выбора и расположения уравнений
<variant>выбора и расположения формул
<variant>булевой функции
<variant>кодирования
92Основной комбинаторной задачей является
<variant>подсчет числа (n,r)- выборок при различных условиях
<variant>подсчет числа (n,r)- выборок при одинаковых условиях
<variant>определение (n,r)- выборок при различных условиях
<variant>определение (n,r)- выборок при одинаковых условиях
<variant>Создание кодов
93Задача о «Кенигсбергских мостах» относится к
<variant>Теории графов
<variant>Транспортной задаче
<variant>кодированию
<variant>комбинаторике
<variant>строительству
94Кодирование — это процесс преобразования данных с целью их
<variant>передачи,сжатия и сохранения от несанкционированного доступа.
<variant>Расчета, анализа и прогнозирования
<variant>передачи,сжатия и открытого доступа.
<variant>передачи,сжатия и сохранения от детей.
<variant>для вечного хранения
95Сжатие данных- это
<variant>алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма
<variant>алгоритмическое преобразование данных, производимое с целью увеличения занимаемого ими объёма
<variant>алгоритмическое преобразование функции, производимое с целью уменьшения занимаемого ими объёма
<variant>процедура для их раскодирования
<variant>необходимая процедура для оптимизации
96Криптография –это
<variant> область знаний о методах обеспечения конфиденциальности и целостности данных
<variant>область знаний о методах обеспечения открытости и целостности данных
<variant>область знаний о методах обеспечения разрушенияданных
<variant>процедура для их раскодирования
<variant>необходимая процедура для оптимизации
97Метод Хаффмана используется для
<variant>Кодирования
<variant>расшифровки
<variant>анализа данных
<variant>расчета данных
<variant>решения решения задач комбинаторики
98Совокупность двух множеств (вершин и ребер) называют
Графом
Отрезком
Функцией
<variant>Петлей
<variant>Сетью
99Если все ребра различны то маршрут называется
Цепью
Функцией
Отрезком
<variant>Петлей
<variant>Сетью
100Утверждение которое либо истинно либо ложно называется
<variant> Высказыванием
<variant>Дискретностью
<variant>Законом
<variant> Мыслью
<variant>Мнением
101Транспортная задача это
<variant> Расчет минимизаций затрат при перевозке груза
<variant>Расчет веса транспортных средств
<variant>Расчет грузоподъемности машин
<variant> Нахождение кратчайших путей при для транспорта
<variant>Нахождение максимальных путей при для транспорта
102Перестановкой элементов Рм множества М
называется ............их в некотором порядке
<variant> Расположение
<variant> Отсутстствие
<variant>Суммирование
<variant>Деление
<variant>Сочетание
103Комбинации, составленные из n данных элементов по k элементов (k<=n, k>0), которые отличаются либо составом элементов, либо порядком расположения элементов это.......
<variant>Размещение
<variant>Перестановка
<variant>Сочетание
<variant>Повторение
<variant>Суммирование
104Сочетанием называется
<variant>неупорядоченное подмножество из k элементов, принадлежащих множеству A.
<variant> упорядоченное подмножество из k элементов, принадлежащих множеству A
<variant>неупорядоченное подмножество из k элементов, непринадлежащих множеству A
<variant>необходимость создания комбинации элементов
<variant>взаимосвязь похожих элементов
105Формула бином Ньютона
(a+b)n=
(a+b)n=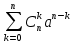
(a)n=
(a+b)n=
(a+b)n=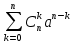
106Под вероятностью понимает
<variant> численную меру появления изучаемого события А
<variant>необходимость учета факторов
<variant>математическую формулу суммирования риска события А
<variant> численную меру непоявления изучаемого события А
<variant>гадание на игровых элементах
107Булевы функции предназначены для работы ........ значениями
<variant> Двоичными
<variant> Ординарными
<variant>Десятичными
<variant>Троичными
<variant>Буквенными
108 Операция конъюнкции предназначена для......
<variant> Умножения
<variant>Деления
<variant> Сложения
<variant>Возведения в степень
<variant>обертки
109Высказывание –это
<variant> некое утверждение о котором можно говорить что оно истинно или ложно
<variant> правило необходимое для совершения операции
<variant>результат который нужен исследователю
<variant>начало проверки гипотезы
<variant>мнение в котором нет пользы
110Граф это совокупность ......
<variant> Ребер и вершин
<variant> Прямых и кривых
<variant>Ребер и точек
<variant>Петлей и точек
<variant>Циклических путей
111Маршрут называется цепью, если
<variant> все вершины различны
<variant>все его ребра различны
<variant> все ребра одинковы
<variant>все вершины одинаковы
<variant>в нем есть петли
112Алгоритм Дейкестры используется для......
<variant>Нахождения кратчайших путей графа
<variant> Нахождения самых долгих путей графа
<variant>Совершения операции дизъюнкции
<variant>Совершения операции конъюнкции
<variant>Совершения операции инверсии
113Транспортная задача- это задача
<variant> которая определяет оптимальный план поставки
<variant> Которая имеет инженерную характеристику
<variant> описывающая графов
<variant>С дифференциальным уравнением
<variant>С интегральным исчислением
114 описывает ...... описывает ......
<variant> Закрытость транспортной задачи
<variant>Оптимальность транспортной задачи
<variant> Открытость транспортной задачи
<variant>Искаженность транспортной задачи
<variant> Многозначность транспортной задачи
115A3=45 означает что.......
<variant> Третий поставщик имеет 45 единиц груза
<variant> Третий потребитель имеет 45 единиц груза
<variant>Тариф третьего маршрута
<variant>Маршрут от от 4-го поставшика 5- му потребителю
<variant>Неправильное обозначение маршрута
116Критический путь описывает ......
<variant>Самый продолжительный путь
<variant>Самый короткий путь
<variant>Самый оптимальный путь
<variant>Неправильный путь
<variant>Самый легкий путь |
 Скачать 179.23 Kb.
Скачать 179.23 Kb.




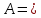 {1,2} B={2,3} тогда А х В=
{1,2} B={2,3} тогда А х В=




 =bjj=1,n означает что
=bjj=1,n означает что 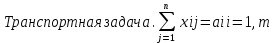 означает что
означает что  означает что
означает что означает что
означает что
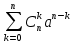

 описывает ......
описывает ......