Тестовые задания по Математике СПО. Тестовые задания по дисциплине Математика ответы. Тестовые задания по дисциплине Математика
 Скачать 24.71 Kb. Скачать 24.71 Kb.
|
|
Тестовые задания по дисциплине Математика 1. Дополнить: Предел отношений приращения функции к приращению аргумента при том, что приращение аргумента стремиться к нулю называется производной функции у= f (х) и обозначается у/ 2. Дополнить: Функция F(x) называется первообразной для функции f (х), если F(x) дифференцируема в любой точке отрезка [a,b] и ее производная равна f (х). 3. Дополнить: Lim [f(x) + g(x)] = Lim f(x) + Lim g(x) x→a x→a x→a Lim [f(x) * g(x)] = Lim f(x) * Lim g(x) x→a x→a x→a f(x) Lim f(x) Lim = , где Lim g(x) = 0 x→a g(x) Lim g(x) 4. Вычислить предел функции lim [(7x+2)(4x-3)(5x+1)] x→1 а) 45 б)54 в)64 г)44 5. Вычислить предел функции lim 3х2+х х → 0 х а)11 б)4 в)3 г)1 6. Наука, изучающая закономерности массовых явлений методом обобщающих показателей называется математическая статистика 7. Норма отпуска омнопона 0,1. Форма выпуска 1% по 1 мл. Больному можно отпустить ампул: а) 1; б) 10; в) 100; г) 5. 8. Норма отпуска пахикарпина 1,2. В одной таблетке содержится 0,1 лекарственного вещества. Больному можно отпустить таблеток: а) 120; б) 60; в) 12; г) 6. 9. После увеличения зарплаты фармацевту за непрерывность стажа работы на 20%,его зарплата составила 2400 руб. Первоначальная зарплата его была: а) 1920 руб; б) 2352 руб; в) 2000 руб; г) 1900 руб. 10. За вредные условия труда работникам аптеки полагается надбавка 15%. Если основной оклад 1200 руб., то зарплата с надбавкой составит: а) 1380 руб; б)1350 руб; в) 1215 руб; г) 180 руб. 11. Растворимость хлорида натрия при 200С составляет 36г. соли в 100г. воды. Масса соли в 340г. насыщенного при этих же условиях раствора: а) 88г; б)122,4г; в) 90г; г) 100г. 12. Концентрация масляного раствора, в 300г. которого содержится 30г. буры, равна: а) 10%; б)15%; в) 30%; г) 9%. 13. Чтобы приготовить 2000мл 0,9% раствора натрия хлорида сухого вещества нужно взять: а) 1,8г; б) 20г; в) 18г; г) 180г. 14. При сушке смородина теряет 80% своего веса. Чтобы получить 5 кг сухой смородины нужно взять свежей смородины: а) 6,25 кг; б) 25 кг; в) 20 кг; г) 10 кг. 15. Из 40 кг свежей черники получается 8 кг сушеной. Чтобы получить 5 кг сушеной нужно взять свежей черники: а) 64 кг; б) 25 кг; в) 10 кг; г) 30 кг. 16.Рассчитайте, какое количество 10% раствора роккала и воды необходимо взять для приготовления 1л 1% раствора: а) 50 мл 10% и 950 мл воды б) 390 мл 10% и 610 мл воды в) 100мл 10% и 900 мл воды г) 220 мл 10% и 780 мл воды 17. Рассчитайте какое количество сухого порошка потребуется для приготовления 400 мл 5% раствора а)0,2 гр. б)2 гр. в)20мг г)20гр. 18. Виды случайных событий (множественный ответ) а)совместные; б)совместимые; в)возвратные; г)противоположные. 19. В ящике 10 пронумерованных шаров с номерами от1 до 10. Вынули один шар. Вероятность того, что номер вынутого шара не превышает 10: а) 0; б) 1/2; в) 9/10; г) 1. 20. Вычислить: 5! +6! 4! а) 11; б) 7/24; в) 1/4; г) 35. 21. В отделе имеются 17 упаковок отечественного производства и 10 упаковок импортного производства некоторого лекарственного препарата. Вероятность того, что наудачу взятая упаковка окажется отечественного производства: а) 17\27; б) 10\17; в)17\10; г)10\27. 22. Найти производную функции f (x) = x3 – 4x + 5 и вычислите ее значение f’ (-1): а) 10; б) -1; в) 2; г) –7. 1 23. Вычислить ∫ 2х2 dx: 0 а) 5; б) 2\3; в) 6-1; г) 0. 24. Найти первообразную функции y = 1/2x: а) y = ¼x2+c; б) y = x3/ 2+c; в) y = 1/6х3+c; г) y = 2 lnx+c. 25.Найти дифференциал функции y = (5x – 3)3: а) dy = 3 (5x – 3)2 dx; б) dy = 15 (5x – 3)2 dx; в) dy = 15 (2x – 3) dx; г) dy = 3 (5x – 3)2 5. 26. Вторая производная y’’(x) функции y(x)= 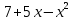 имеет вид: имеет вид:а) y’’=-2 , б)y’’=11, в) y’’=5-2x , г)y’’=0 27. Дифференциал функции y= 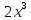 +7x +7xа) 6 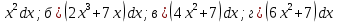 28. Дополнить: Операция интегрирования является обратной операции дифференцирования. 29. Определите ДЖЕЛ для мужчины 30 лет ростом 180 см: а) 5.1; б) 3.25;в)4.9; г)5,3 30. Вычислите массу семимесячного ребенка, если он родился с весом 3,5 кг а) 7,5; б) 8,4; в)7.9; г)8,3 |
