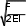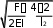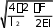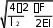цуыв. Тестовые задания по разделам изучения содержания дисциплины
 Скачать 250.83 Kb. Скачать 250.83 Kb.
|
В: ФАЙЛ +y x, Аch xcos exp 2     l 4EI l 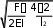 4EI F 42 2 4EI F 42 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 y | F | 2 y | | y | | | F | | |
| x4 4 y | F | x2 2 y | | | y | | | R 0 | |
| x4 4 y | F | x2 2 y | | | y | | | F | |
| x4 4 y | F | x2 2 y | | | y | | | R F | |
| x4 | | x2 | | | | | | R | |
В: ФАЙЛ + EIВ: ФАЙЛ - EIВ: ФАЙЛ - EIВ: ФАЙЛ - EI
ВЫБОР
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие поездов, имеет вид …
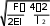 x
x 4EI F
42 2
l2
4x2
В: ФАЙЛ +
y x, Ach
xcos exp
1 2
l
4EI l 8R l
2
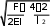 4EI F
4EI F 42 2
l2
4x2
В: ФАЙЛ -
y x, Ach
xexp
1 2
4EI l
8R l
2
2
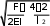 x
x 4EI F
42 2 l2
В: ФАЙЛ -
y x, Ach
xcos exp
l
4EI l 8R
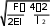
В: ФАЙЛ -
xl2
4x2
y x, Ach
xcos l
8R1 l2
ВЫБОР
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в бесстыковом пути для модели, учитывающей воздействие поездов для точки х = 0 …
4EI F 42 2 l2
2
В: ФАЙЛ +
y0,
f0 exp




4EI l 8R
4EI F2 l2



В: ФАЙЛ -
y0,
f0 exp
4EI
8R
4EI F 42 l2
В: ФАЙЛ -
y0,
f0 exp
4EI l2
8R




4EI F 42 2 l2
2
В: ФАЙЛ -
y0, exp




4EI l 8R
ВЫБОР
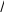 Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в бесстыковом пути для модели,
Решение дифференциального уравнения изменений поперечных перемещений под действием продольных сжимающих сил в бесстыковом пути для модели,учитывающей воздействие поездов для точки х = 0 при
l2 42EIF…
6, 25F2 2EI
В: ФАЙЛ +
y0,
f0 exp
EI
2RF


6, 25F2 2EI
В: ФАЙЛ -
y0,
f0 exp
EI
2RF


6, 25F2 EI
В: ФАЙЛ -
y0,
f0 exp
EI
2RF


6, 25F2
2EI
В: ФАЙЛ -
y0, exp
EI
2RF


ВЫБОР
Опасная скорость роста стрелы изгиба рельсов в плане определяется по формуле
…
6, 25 fF2 6, 25F2
В: ФАЙЛ +
y0, 0 exp
EI

EI
В: ФАЙЛ -
y0,
6, 25F2
 EI
EIexp
6, 25F2

EI
6, 25 fF2 6, 25F2
В: ФАЙЛ -
y0, 0 exp
EI

EI
6, 25 fF2 6, 25F2
В: ФАЙЛ -
y0, 0 exp
 EI EI
EI EIРаздел 03_Математические модели состояния и процессов в пределах статики, применяемые в расчетах объектов железнодорожной инфраструктуры
ВЫБОР
Величина концевого участка упругого стержня в пластической среде в статике определяется …
В: ФАЙЛ + l
Ft Rн

k r
В: ФАЙЛ - lk
В: ФАЙЛ - lk
Ftr
 Rн
Rн
r
F R2
В: ФАЙЛ - l t н

k r
ВЫБОР
При экспериментальной степенной зависимости погонного сопротивления, среднее rcp находится по формуле …
max
abd
r rcp 0
В: ФАЙЛ + max
max
bd
В: ФАЙЛ -
r rcp
0
max
max
ad
r rcp 0
В: ФАЙЛ - max
В: ФАЙЛ -
r rcp
max
ab
0
max
ВЫБОР
Необходимую подъемную силу для изгиба упругого стержня можно определить по формуле …
В: ФАЙЛ +
2 4 EJf ql
P
l3 2
В: ФАЙЛ -
2 4 EJf ql
P
В: ФАЙЛ - В: ФАЙЛ -
l3
2 4 Ef
P
l3
2 4 Jf
P
l3
2
ql
2
ql
2
ВЫБОР
Математическое выражение принципа Лагранжа …
n
В: ФАЙЛ + dAi 0
i
n
В: ФАЙЛ - Ai 0
i
n
В: ФАЙЛ - dA 0
n
i
В: ФАЙЛ - A 0
i
ВЫБОР
Выражение элементарной работы dA1внешней силы Рна перемещении df…
В: ФАЙЛ +
dA1 Рdf
В: ФАЙЛ - dA Рdf
В: ФАЙЛ - В: ФАЙЛ -
A1 РdfdA1 Рf
Работа распределенных сил сопротивления поперечным перемещениям q на длине изогнутого участка упругого стержня …
В: ФАЙЛ + dA qldf

2 2
В: ФАЙЛ - dA qdf

2 2
В: ФАЙЛ - dA qldf

2 4
В: ФАЙЛ - dA ldf

2 2
ВЫБОР
Работа сил погонного сопротивления продольным перемещениям раскрепленного участка упругого стержня на длине L…
В: ФАЙЛ + В: ФАЙЛ - В: ФАЙЛ - В: ФАЙЛ -
dA3 рLd
dA3 рd dA3 Ld dA3 рL
ВЫБОР
Работа внутренних сил изгиба упругого стержня находится …
В: ФАЙЛ +
dA4
2 4 ЕJf
l3 df
В: ФАЙЛ -
dA4
2 4 ЕJ
l3 df
В: ФАЙЛ -
dA4
2 4 Jf
l3 df
В: ФАЙЛ -
dA4
2ЕJfdfl3
ВЫБОР
Условия равновесия выражения бесконечно малого участка упругого стержня dx…
В: ФАЙЛ + F dF F rdx
В: ФАЙЛ - F dF rdxВ: ФАЙЛ - dF F rdxВ: ФАЙЛ - F dF F dx
Дифференциальное уравнение продольных сил в упругом стержне в пластичной среде в статике …


d2 r
В: ФАЙЛ +
dx2 E


d2 r
В: ФАЙЛ -
dx2 E
В: ФАЙЛ -
d2 r

 dx2
dx2 d2 r


В: ФАЙЛ -
d2 E
ВЫБОР
Формула для определения зазора в упругом стержне в статике …
В: ФАЙЛ +
2 Е t2
2r
В: ФАЙЛ -
В: ФАЙЛ -
2 Е t
2r
2 Еt2
2r
В: ФАЙЛ -
Е t2
2r
ВЫБОР
Значение дополнительной продольной силы F, возникающей в упругом стержне при его изгибе на ограниченном участке …
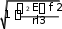 rl
rl В: ФАЙЛ +
F
 2
2 1
В: ФАЙЛ -
rl

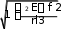 F 2
F 2
 rl
rl В: ФАЙЛ - F
 2
2 1
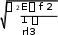 r
r  В: ФАЙЛ - F
В: ФАЙЛ - F 2
1
Значение дополнительной продольной силы F, возникающей в упругом стержне на ограниченной длине, имеющей кривизну …
В: ФАЙЛ +
F rL