Ток. Типовые звенья сау
 Скачать 298.93 Kb.
|
|
Типовые звенья САУ. Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями. В теории выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а, следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев. К простейшим типовым звеньям относятся: усилительное, инерционное (апериодическое 1-го порядка), интегрирующие (реальное и идеальное), дифференцирующие (реальное и идеальное), апериодическое 2-го порядка, колебательное, запаздывающее. 1) Усилительное звено. Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(р) = К. Параметр К называетсякоэффициентом усиления. Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рис. 1.18).  Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.  Интегрирующее.Идеальное интегрирующее. Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.  ; W(s) =  При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает (см. рис. 1.19) Это звено астатическое, т.е. не имеет установившегося режима. Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться. Реальное интегрирующее. Передаточная функция этого звена имеет вид: W(s) =  . Дифференцирующее.) Идеальное дифференцирующее. Выходная величина пропорциональна производной по времени от входной:  ; W(s) = K*s Реальное дифференцирующее. И  деальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям, передаточные функции которых вид:W(s) =  .Пример звена: электрогенератор. Входной параметр – угол поворота ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то на клеммах появится напряжение, но если ротор далее не вращать, напряжение снизится до нуля. Резко упасть оно не может вследствие наличия индуктивности у обмотки. Апериодическое (инерционное). Этому звену соответствуют ДУ и ПФ вида: 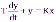 ; W(s) =  .Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х0.  y(t) = K x0 (1 -  ).Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.22). Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.22). Звенья второго порядка З  венья имеют ДУ и ПФ вида ,W(s) =  .При подаче на вход ступенчатого воздействия амплитудой х0 на переходная кривая будет иметь один из двух видов: апериодический (при Т1 2Т2) или колебательный (при Т1 < 2Т2). В связи с этим выделяют звенья второго порядка: апериодическое 2-го порядка (Т1 2Т2), инерционное (Т1 < 2Т2), консервативное (Т1 = 0). Запаздывающее. Если при подаче на вход объекта некоторого сигнала он реагирует на этот сигнал не моментально, а спустя некоторое время, то говорят, что объект обладает запаздыванием. Запаздывание – это интервал времени от момента изменения входного сигнала до начала изменения выходного. :Запаздывающее звено – это звено, у которого выходная величина у в точности повторяет входную величину х с некоторым запаздыванием y(t) = x(t -) Передаточная функция звена: W(s) = e-р. Примеры запаздываний: движение жидкости по трубопроводу (сколько жидкости было закачано в начале трубопровода, столько ее выйдет в конце, но через некоторое время, пока жидкость движется по трубе), движение груза по конвейеру (запаздывание определяется длиной конвейера и скоростью движения ленты) и т.д.. |