Лабораторная работа №2
Традиционные симметричные криптосистемы.
Цель работы – закрепление теоретических знаний по методам криптоанализа симметричных криптосистем и практическое освоение методов криптоанализа криптосистем гаммирования с периодической гаммой на примере криптосистемы Виженера.
Время - 4 часа.
1 Основные расчетные соотношения
Криптосистема Виженера представляет собой шифр гаммирования с использованием периодической гаммы малого периода. В криптосистеме
Виженера ключ kd
задается набором из d символов. Такие наборы
подписываются под открытым текстом x1, x2 ,..., xn,
xi Am, до получения
- число полных периодов
kd, r
nmod d.
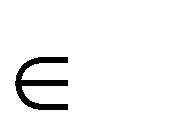 Уравнение шифрования для криптосистемы Виженера:
 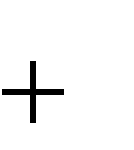 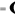  
ki
mod m
уi xi .
При дешифровании криптосистемы Виженера решаются две
взаимосвязанные задачи:
задача определение периода dключевой последовательности k;
задача дешифрования криптограммы Yпри известном периоде dдлине
 
.
k
ключевой последовательности
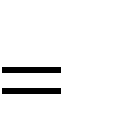 Основным инструментом решения задачи определения периода ключевой последовательности криптосистемы Виженера являются методы Фридмана, основанные на понятии индекса совпадения. Индексом совпадения Основным инструментом решения задачи определения периода ключевой последовательности криптосистемы Виженера являются методы Фридмана, основанные на понятии индекса совпадения. Индексом совпадения
последовательности Х
х1, х2 ,..., хп
называется величина
 ( Х) mFi (Fii1 n( n1) , (1) 1) 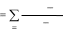 где ХAm- некоторая последовательность; Fi- частота встречаемости 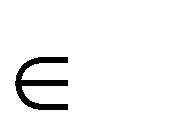 (число (число мест в тексте) i- буквы в последовательности Х. Для криптосистемы Виженера, получаемого шифрованием открытого 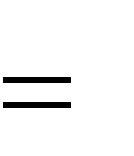 текста X a, a,..., a с помощью равновероятного выбора ключа из   K n K n1 2 n k 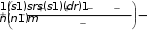    множества всех локально-периодических последовательностей справедливо dпериода dи  M (Y M (Y) ( s 1)srs( sn( n1)(d1) r) 2 pi i pi i. (2) 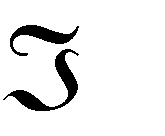 Первый метод Фридмана Первый метод Фридмана состоит в том, что вычисляется индекс
совпадения
(Y)
для имеющейся криптограммы в соответствии с выражением
 (1) и затем его значение сравнивается с (2) при d 1,2,3,... . При достаточной 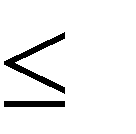 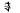 близости индекса совпадения к одному из значений (2), при некотором d, предполагают, что период равен этому значению d. Первый метод Фридмана
эффективен для d
5, т.к. значение M
(Y)
для фиксированного периода d
совпадает со значениями целого ряда различных периодов ключевой последовательности. Суть второгометодаФридманасостоит в опробовании возможных 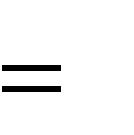 периодов dпо следующей схеме. Из исходной криптограммы Y y1, y2 ,..., ynдля предполагаемого периода dключевой последовательности выписывается 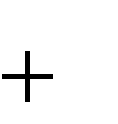 d dподпоследовательностей: 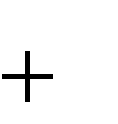  d d1) y1, y1 , y12d,... 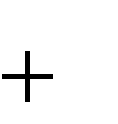  d d2) y2 , y2 , y22d,...   ..............  dd dd) yd, yd  , yd2d , yd2d,...
 Для каждой подпоследовательности подсчитывается ее индекс Для каждой подпоследовательности подсчитывается ее индекс
совпадения
(Yd) . Если все индексы совпадения в среднем близки к значению
   p i1 2 p i1 2 (среднее значение индекса совпадения случайных криптограмм, diполученных с помощью гамм периода 1), то принимают величину dза истинный период, в противном случае опробуется следующая величина периода. Второй метод Фридмана позволяет эффективно определять периоды 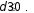   Метод «протяжки» вероятного слова Метод «протяжки» вероятного слова. При известном периоде ключевой последовательности dвыписываются две подпоследовательности исходной криптограммы:
y1, y2,..., yi,...y(k
1)d r;
   y1 y1 , y2,..., yi,..., ykd r, nkd r.       Формируется называемое «множество вероятных слов», которые, по мнению криптоаналитика, могут быть началом искомого открытого текста.
Для слова
a1 , a2 ,..., ar
из этого множества, находятся первые символы
      вероятного слова, а, следовательно, и первых символов ключевой последовательности, проверяется на «читаемость» следующего фрагмента расшифрованного текста   f 1( y1k1d),f 1 f 1( y1k1d),f 1( y2 k2d k2d),..., f1( yrkrd) .    Если полученная последовательность символов «читаемая», то полагают,
что
k1 , k2 ,..., kr
k1 , k2 ,..., kr, т.е. найдены первые r символов ключевой
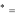 последовательности. Далее анализируя фрагменты расшифрованной криптограммы, ищут возможные продолжения открытого текста, таким образом, чтобы получить недостающую часть ключевой последовательности 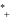 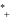 kr1, kr2 kr1, kr2,..., kdkr1, kr2,..., kd.   После того, как определен весь ключ, оставшаяся часть криптограммы расшифровывается на найденном ключе. Если же последовательность символов принимается как случайная (т.е. «нечитаемая»), то опробуется следующее вероятное слово. Вероятные слова могут выбираться также из предположения, что они является окончанием открытого текста или, в общем случае, располагаются на других позициях открытого текста. Методчтениявколонках. Рассмотрим два случая:
априорные вероятности символов ключевой последовательности не известны;
априорные вероятности символов ключевой последовательности известны.
Априорные вероятности символов ключевой последовательности не
известны. Пусть дана криптограмма Y
y1, y2 ,..., yn. Известен период
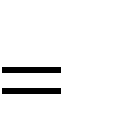  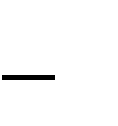 ключевой последовательности d. Сформируем две подпоследовательности исходной криптограммы
y1, y2,..., yi,...y(k
1)d r;
 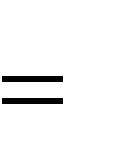  y1 y1 , y2,..., yi,..., ykd r, nkd r.  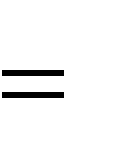   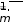 Будем полагать, что открытыми текстами, подлежащими шифрованию, являются содержательные тексты с известными вероятностями букв алфавита
P(aj)
pj, j
, где j- порядкоый номер буквы алфавита. Также будем
считать, что на множестве Kзадано равномерное распределение, т.е. ключом является реализация выборки объемом dиз равномерного распределения K.      Тогда вероятность Тогда вероятность того, что i-я и ( i d)-я буквы открытого текста были равны
соответственно,
xi и
xi d
, при условии, что i-я и ( i
d)-я буквы
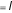 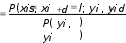 криптограммы равны соответственно, yiи yiопределяется выражением 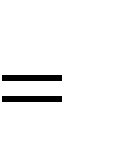 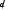 P P( xis, xi| yi, yi ) . 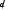 P P( xis, xi| yi, yi ) sl.
Для каждой пары
yiи yi
букв исходной криптограммы упорядочим в
соответствии с убыванием полученных значения условных вероятностей (5) пары букв открытого текста s и l . Построив такие колонки для каждого i , в результате получаем таблицу (табл. 1), в которой верхние пары имеют большую условную вероятность, чем нижние.       Таблица 1.
i 1
|
…
|
i j
|
…
|
i n
|
y1
y1 d
|
…
|
yj
yjd
|
…
|
y(k1)dr
ykdr
|
….
|
…
|
xjs, p
xj d l sl
|
…
|
…
|   Буквы искомого содержательного текста будут находится вероятнее всего в первых строках и задача сводится к подбору таких пар букв, чтобы в результате получался осмысленный текст. Априорныевероятностисимволовключевойпоследовательностиизвестны. Если априорно известны вероятности символов ключевой
последовательности, то задача дешифрования криптограммы аналогична задаче
восстановления текста, зашифрованного неравновероятной гаммой. Пусть
рi,
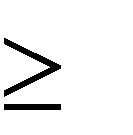 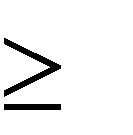 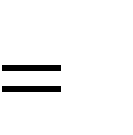 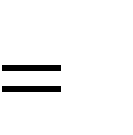 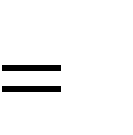 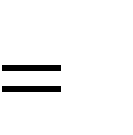 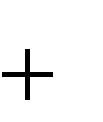   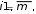 есть вероятность использования символа в ключевой последовательности. Рассмотрим простую задачу, когда некоторые символы вовсе не встречаются в ключевой последовательности. Положим, что 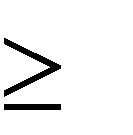 р1 р2 р1 р2... рl, plpl 2 ... pm0 , l m.  Составим таблицу (см. таблицу 2), в которой по строкам расположены символы, полученные путем расшифровки криптограммы одним символом
ключевой последовательности
ki , i
. Задача заключается в подборе по
столбцам символов таким образом, чтобы в результате получился осмысленный текст. Если нельзя исключить использования ни одного символа в ключевой последовательности, то тогда поступают следующим образом. Для составления 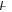 таблицы исключают из рассмотрения m наименее вероятных букв алфавита, дальнейшие действия аналогичны рассмотренным выше. Надежность такого метода меньше, так как не исключена возможность частичной, а может и полной, потери истинного открытого текста. Таблица 2.
ki yi
|
y1
|
….
|
….
|
yn
|
k1
|
yˆ1(k1)
|
….
|
…..
|
yˆn(k1 )
|
k2
|
yˆ1 (k2 )
|
….
|
….
|
yˆn(k2 )
|
….
|
….
|
….
|
….
|
….
|
kl
|
yˆ1(kl)
|
….
|
….
|
yˆn(kl)
| Порядок выполнения работы
При подготовке к лабораторной работе
На этапе подготовки к лабораторной работе студенты должны, используя литературу [1,2,3,4], материалы лекций углубить свои знания по следующим вопросам: криптосистема Виженера; методы определения периода ключевой последовательности; методы бесключевого чтения (метод «протяжки» вероятного слова, метод чтения в колонках). Студенты на предстоящее лабораторное занятие готовят алфавиты русского и английского языка со значениями вероятностей встречаемости символов.
Во время проведения занятия
Преподаватель перед проведением занятия проводит контрольный опрос студентов и определяет степень их готовности к лабораторной работе. Затем преподаватель разбивает группу студентов на подгруппы по два человека. Каждая подгруппа получает от преподавателя индивидуальный вариант задания на лабораторную работу, который представляет собой криптограммы, зашифрованные с помощью криптосистемы Виженера.
Лабораторная работа состоит из двух частей. В первойчастиработы студенты дешифрируют первую заданную криптограмму с использованием первого метода Фридмана и метода чтения в колонках. При этом студенты должны: определить период ключевой последовательности с помощью первого метода Фридмана; используя метод чтения в колонках для заданного случая дешифрировать первую криптограмму. Втораячастьработы заключается в дешифровании второй криптограммы с применением второго метода Фридмана и метода «протяжки» вероятного слова. На этом этапе студенты должны: используя второй метод Фридмана определить период ключевой последовательности; на основании вычисленного значения периода ключевой последовательности используя метод «протяжки» вероятного слова дешифрировать вторую криптограмму.
Если в результате дешифрирования заданных криптограмм получены осмысленные тексты, студенты оформляют отчет и представляют его преподавателю.
Содержание отчета
Отчет должен включать в себя следующие пункты:
Задание на выполнение лабораторной работы (исходные криптограммы).
Основные расчетные соотношения.
Результаты расчетов, представленные в виде табл. 1 и 2.
Результаты анализа, т.е. дешифрованные криптограммы.
Контрольные вопросы
Основные понятия криптографии и криптоанализа.
Методы Фридмана.
Метод «протяжки» вероятного слова, метод чтения в колонках.
Понятие индекса совпадения.
Криптосистема Виженера.
Связь криптосистемы Виженера с другими простейшими криптосистемами.
Литература
Рябко Б.Я., Фионов А.Н. Криптографические методы защиты информации. Учебное пособие для вузов. М.: Горячая линия – Телеком, 2005.
Баричев С.Г, Гончаров В.В., Серов Р.Е. Основы современной криптографии: Учебный курс. – 2-е изд. – М.: Горячая линия – Телеком, 2002.
Осипян В.О, Осипян К.В. Криптография в задачах и упражнениях. – М.: Гелиос АРВ, 2004.
Харин Ю.С., Беник В.И, Матвеев Г.В., Агиевич С.В. Математические и компьютерные основы криптологии: Учеб. пособие. – Минск: Новое знание, 2003.
|
 Скачать 329.56 Kb.
Скачать 329.56 Kb.
 Буквы искомого содержательного текста будут находится вероятнее всего в первых строках и задача сводится к подбору таких пар букв, чтобы в результате получался осмысленный текст.
Буквы искомого содержательного текста будут находится вероятнее всего в первых строках и задача сводится к подбору таких пар букв, чтобы в результате получался осмысленный текст.
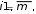 есть вероятность использования символа в ключевой последовательности. Рассмотрим простую задачу, когда некоторые символы вовсе не встречаются в ключевой последовательности. Положим, что
есть вероятность использования символа в ключевой последовательности. Рассмотрим простую задачу, когда некоторые символы вовсе не встречаются в ключевой последовательности. Положим, что Составим таблицу (см. таблицу 2), в которой по строкам расположены символы, полученные путем расшифровки криптограммы одним символом
Составим таблицу (см. таблицу 2), в которой по строкам расположены символы, полученные путем расшифровки криптограммы одним символом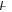 таблицы исключают из рассмотрения m наименее вероятных букв алфавита,
таблицы исключают из рассмотрения m наименее вероятных букв алфавита,


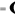




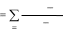 где
где

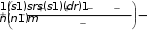
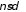
 множества
множества M
M 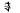 близости
близости


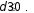
 y1 ,
y1 , вероятного
вероятного Если
Если последовательности.
последовательности.
 Будем
Будем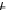

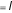
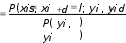 криптограммы
криптограммы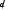 P(xi
P(xi




 Таблица 1.
Таблица 1.