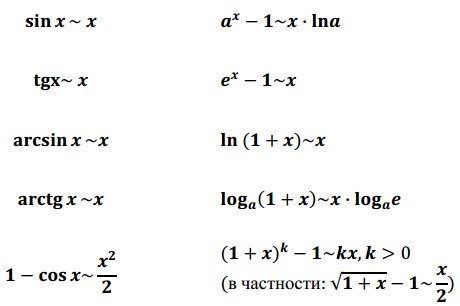МОДУЛЬ 1: Элементарные функции и пределы
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности. Теорема о единственности предела сходящийся последовательности(с доказательством).
Последовательностью называется числовая функция, определенная на множестве натуральных чисел.
Число A называется пределом числовой последовательности {an}, если для любого, даже сколь угодно малого положительного числа ε > 0, найдется такое число N (зависящее от ε), что для всех членов последовательности с номерами n > N верно неравенство: |an - A|< E.
Последовательность, которая имеет предел, называется сходящейся, в обратном случае последовательность расходится.
Теорема о единственности предела сходящийся последовательности: Последовательность не может иметь больше одного предела. Доказательство. Это следует из того, что последовательность не
может одновременно приближаться к двум разным числам одновременно.
Формально, выберем ε значительно меньше разницы между числами A и B.
Тогда очевидно, что мы не сможем указать такого номера N, начиная с
которого одновременно будут выполнены два условия: |an - A|< E и |an - В|< E
Этими рассуждениями теорема доказана.
Ограниченная числовая последовательность. Теорема об ограниченности сходящийся числовой последовательности. Признак Вейерштрасса сходимости монотонной последовательности (формулировка).
Последовательность ограничена, если найдется такое положительное число, для которого все члены последовательности по модулю окажутся не больше этого числа. {an}- ограничена, если существует М>0: |an|<= M любой n принадл. N

Теорема Вейерштрасса. (Основная теорема теории последовательностей). Если последовательность {an} является нестрого возрастающей (нестрого убывающей) и {an} ограничена сверху (снизу), то {an} является сходящейся. Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность {an} имеет предел.
Определения по Коши конечного и бесконечного предела функции в точке и на бесконечности. Односторонние пределы функции. Определение предела функции по Гейне. Теорема о связи двустороннего предела функции в точке с односторонними пределами (с доказательством).
Предел функции в бесконечности: Число A называется пределом функции y=f(x) при x стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного ε, найдется такое число M(зависящее от ε), что для всех x таких, что |x|>M, выполнено неравенство: |f(x) - A|< ε.
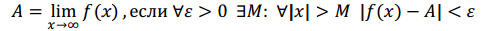
Предел функции в точке:Число A называется пределом функции y = f(x) при x → a, если для любого, даже сколь угодно малого положительного для любого, даже сколь угодно малого ε > 0, найдется такое число δ > 0 (зависящее от ε), что для всех x из δ-окрестности точки a, выполнено неравенство: |f(x) - A|< ε.
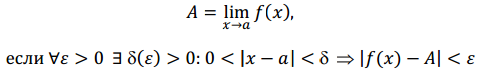
Односторонние пределы: Пределом функции f(x) в точке x=a слева называется предел, вычисляемый в предположении, что x → a, оставаясь все время меньше значения a. Аналогично, пределом справа называется предел функции f(x) при x → a, при том, что x > a. Односторонние пределы обозначаются так:
 Односторонним пределом функции называется предел справа или предел слева. Односторонним пределом функции называется предел справа или предел слева.
По Гейне: Число b называется пределом функции f(x) в точке a, если для любой последовательности {xn} прин D(f), которая сходится к , соответствующая последовательность значений функции {f(xn)} сходится к b.
Теорема о единственности предела функции(с доказательством).
Теорема: Последовательность точек расширенной числовой прямой R может иметь на этой прямой только один предел.
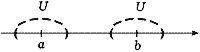 Допустим противное. Пусть существует такая последовательность xn прин. R , n = 1, 2, ..., что Допустим противное. Пусть существует такая последовательность xn прин. R , n = 1, 2, ..., что  = a и = a и  = b, причем a не равно b, a прин. R , b прин. R . Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b : U = b, причем a не равно b, a прин. R , b прин. R . Возьмем какие-либо непересекающиеся окрестности U = U(а) и V = V(b) точек а и b : U  V = V = 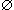 . Согласно определению предела вне окрестности U точки а, в частности в окрестности Vточки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие. . Согласно определению предела вне окрестности U точки а, в частности в окрестности Vточки b, содержится лишь конечное число членов последовательности {xn}. Однако точка b также является ее пределом, и потому в ее окрестности V должны находиться все члены последовательности {xn}, начиная с некоторого номера, а следовательно, бесконечно много ее членов. Получилось противоречие.
Ограниченные и локально ограниченные функции. Теорема о локальной ограниченности функции, имеющей конечный предел( с доказательством).
Локально ограниченная -- это значит ограниченная на каком-то множестве аргументов, то есть можно указать такие значения a и b, что a <= f(x) <= b для любого x из этого множества.
Теорема (локальная ограниченность функции, имеющий предел).Если предел f(x) при x → x0 равняется А, то найдется окрестность x0 , во всех точках которых функция f(x) ограниченна. Положим ε = 1. Из условия теоремы следует существование окрестности:  . Следовательно: . Следовательно:  
Отсюда для указанных х 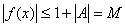 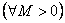 что и означает ограниченность f(x) в что и означает ограниченность f(x) в  . .
Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой ( с доказательством).
Функция y=f(x) называется бесконечно малой при x → x0 если , 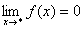 По определению предела функции это равенство означает, что для любого числа ε > 0 найдется число б = б(ε) > 0 , такое, что для всех x, удовлетворяющих неравенству 0 <|x-x0|<б, выполняется неравенство |f(x)| < ε. По определению предела функции это равенство означает, что для любого числа ε > 0 найдется число б = б(ε) > 0 , такое, что для всех x, удовлетворяющих неравенству 0 <|x-x0|<б, выполняется неравенство |f(x)| < ε.
Запишем это определение, используя логическую символику: 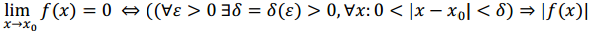 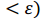
Теорема: Для того, чтобы функция  , определённая в , определённая в  имела конечный предел при x → a, необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при x → a ( имела конечный предел при x → a, необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при x → a ( , где , где  - б.м.ф. при x → a). - б.м.ф. при x → a).
Доказательство: I Необходимость:
Дано: 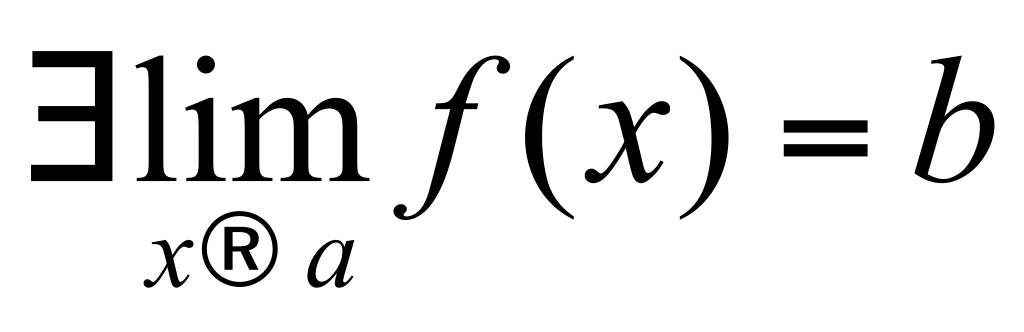 Доказать: Доказать: 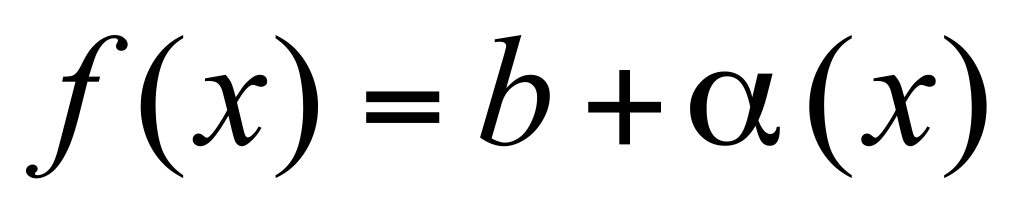 , где , где  - б.м.ф. при x → a. - б.м.ф. при x → a.
 Пусть Пусть 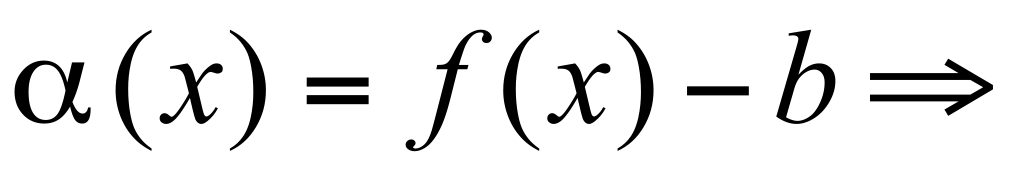 по определению б.м.ф по определению б.м.ф 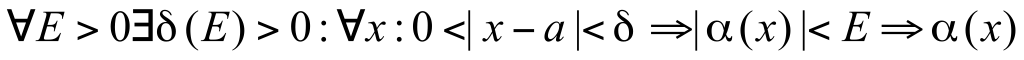 - б.м.ф. при x → a. - б.м.ф. при x → a.
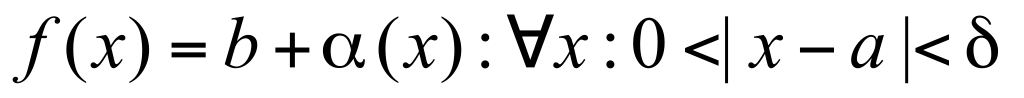 II Достаточность: Дано: II Достаточность: Дано: 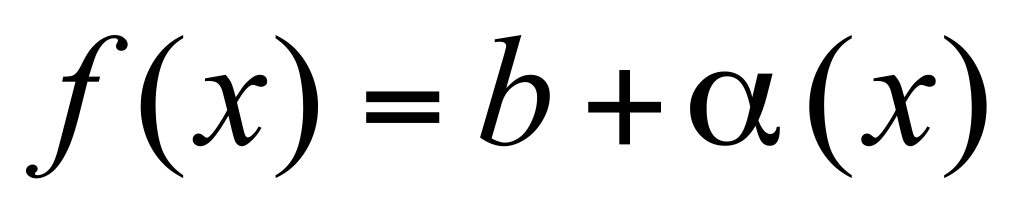 , где , где  - б.м.ф. - б.м.ф.
при x → a. Доказать: 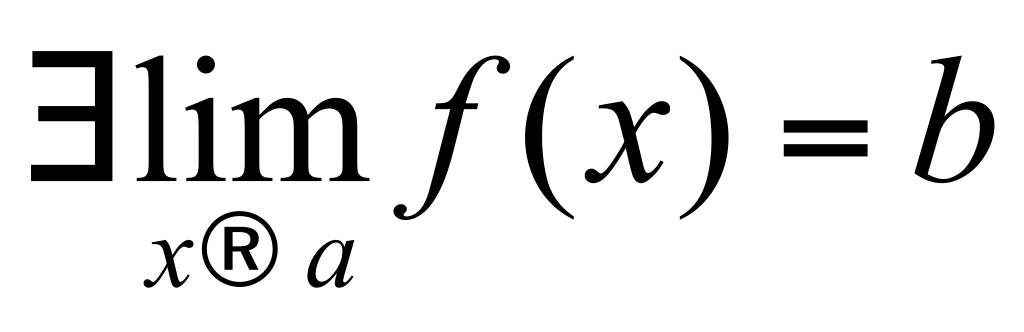
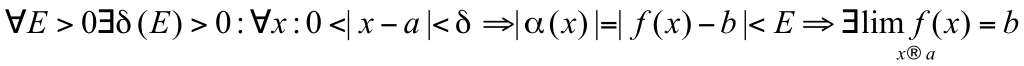
Теорема о сумме конечного числа бесконечно малых функций ( с доказательством). Теорема о произведении бесконечно малой на ограниченную (с доказательством).
Теорема (сумма бесконечно малых величин). Если функции а(х) и δ(х) являются бесконечно малыми, то их сумма а(х) + δ(х) -бесконечно малая. Доказательство. Пусть ε - произвольное положительное число. Так
как функции а(х) и δ(х) бесконечно малые, то найдутся такие числа δ1 и δ2,
что при 0 < |x-a|< δ1 и 0 < |x-a|< δ2 имеют место неравенства: 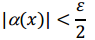 
Обозначим через δ наименьшее из двух чисел δ1 и δ2. Тогда при 0 < |x-a|< δ будет выполнено: 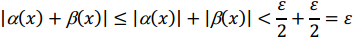 Этим доказано, что для любого ε > 0 существует такое число δ > 0, что при 0 < |x-a| < δ выполнено неравенство: |а(х) + δ(х)| < ε, сумма бесконечно малых есть бесконечно малая. Следствием теоремы является ее распространение на случай алгебраической суммы любого конечного числа бесконечно малых. Этим доказано, что для любого ε > 0 существует такое число δ > 0, что при 0 < |x-a| < δ выполнено неравенство: |а(х) + δ(х)| < ε, сумма бесконечно малых есть бесконечно малая. Следствием теоремы является ее распространение на случай алгебраической суммы любого конечного числа бесконечно малых.
Теорема (произведение бесконечно малой величины на ограниченную величину). Произведение бесконечно малой величины на ограниченную величину есть бесконечно малая величина. Доказательство. Пусть f(x) – ограниченная при x → a функция, а а(х) бесконечно малая. Тогда существует такое число M > 0, что  для всех x, достаточно близких к a. Для ε > 0 существует δ > 0, что при условии 0 < |x-a| < δ одновременно выполняются неравенства: для всех x, достаточно близких к a. Для ε > 0 существует δ > 0, что при условии 0 < |x-a| < δ одновременно выполняются неравенства:   Составим произведение: Составим произведение:  Этим доказано, что произведение бесконечно малой на ограниченную величину есть бесконечно малая. Этим доказано, что произведение бесконечно малой на ограниченную величину есть бесконечно малая.
Бесконечно большие функции. Теорема о связи бесконечно малой и бесконечно большой функции ( с доказательством).
Функция y = f(x) называется бесконечно большой величиной при x → a (или при x → ∞), если для любого, даже сколь угодно большого числа M > 0 найдется δ (зависящее от M), что для всех x таких, что 0 < | x – a |< δ,
выполнено неравенство: | f (x)| > M. Бесконечно большая величина больше любого наперед взятого большого числа. Бесконечно большой величиной называется переменная величина, абсолютное значение которой неограниченно возрастает.
Теорема (связь между бесконечно малыми и бесконечно большими величинами).
(1) Если α (x) – бесконечно малая, то 1/ α (x) бесконечно большая.
Если β (x) – бесконечно большая, то 1/ β (x) бесконечно малая.
Доказательство. (1) Выберем M > 0 и обозначим 1/ M = ε. Так как α (x) бесконечно малая, то числу ε > 0 соответствует δ > 0 такое, что при 0 < |x-a| < δ выполняется неравенство: 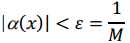 Следовательно, Следовательно, 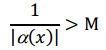 Эта величина является бесконечно большой. (2) Выберем ε > 0 и обозначим 1/ε = М. Так как β(х) бесконечно большая, то числу M соответствует δ > 0, такое, что при 0 < |x-a| < δ выполняется неравенство: Эта величина является бесконечно большой. (2) Выберем ε > 0 и обозначим 1/ε = М. Так как β(х) бесконечно большая, то числу M соответствует δ > 0, такое, что при 0 < |x-a| < δ выполняется неравенство: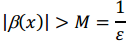 Следовательно, Следовательно, 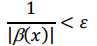 Эта величина является бесконечно большой. Эта величина является бесконечно большой.
Теорема о пределе суммы, произведения и частного функции (доказательство для функции и последовательности).
1)Предел суммы двух функций равен сумме их пределов: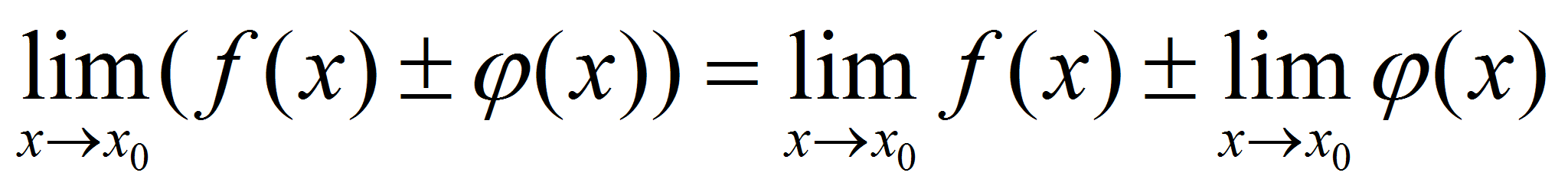 Доказательство: Пусть Доказательство: Пусть 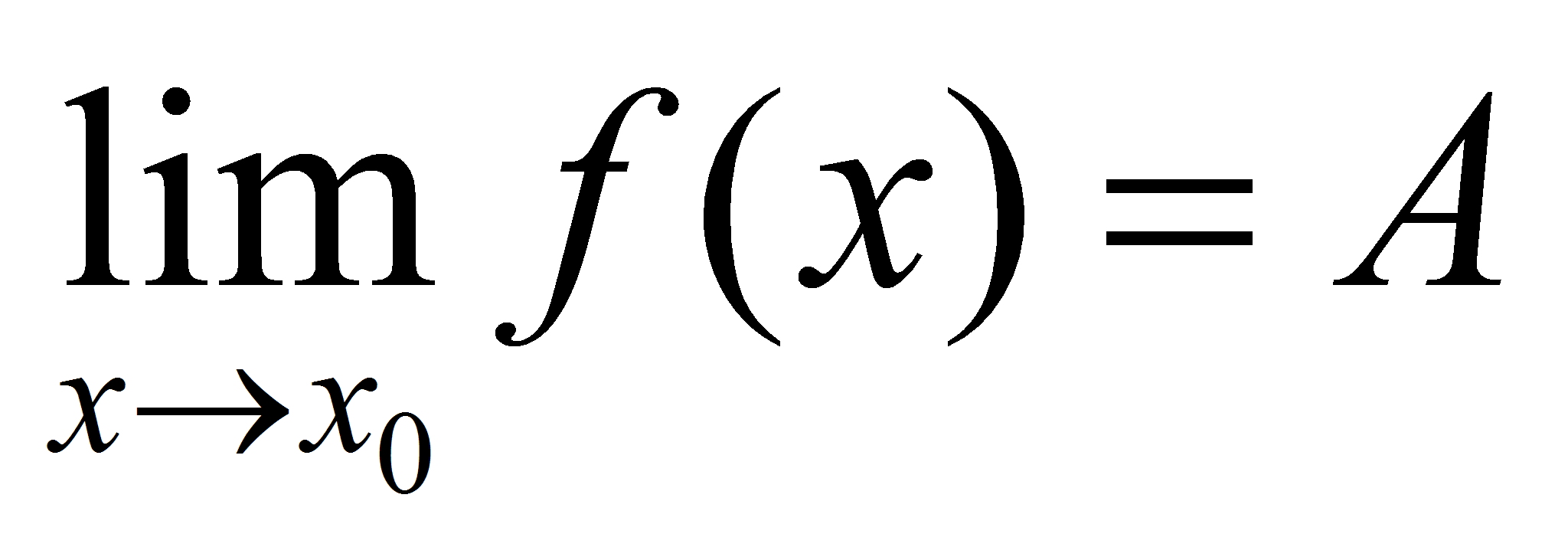 , ,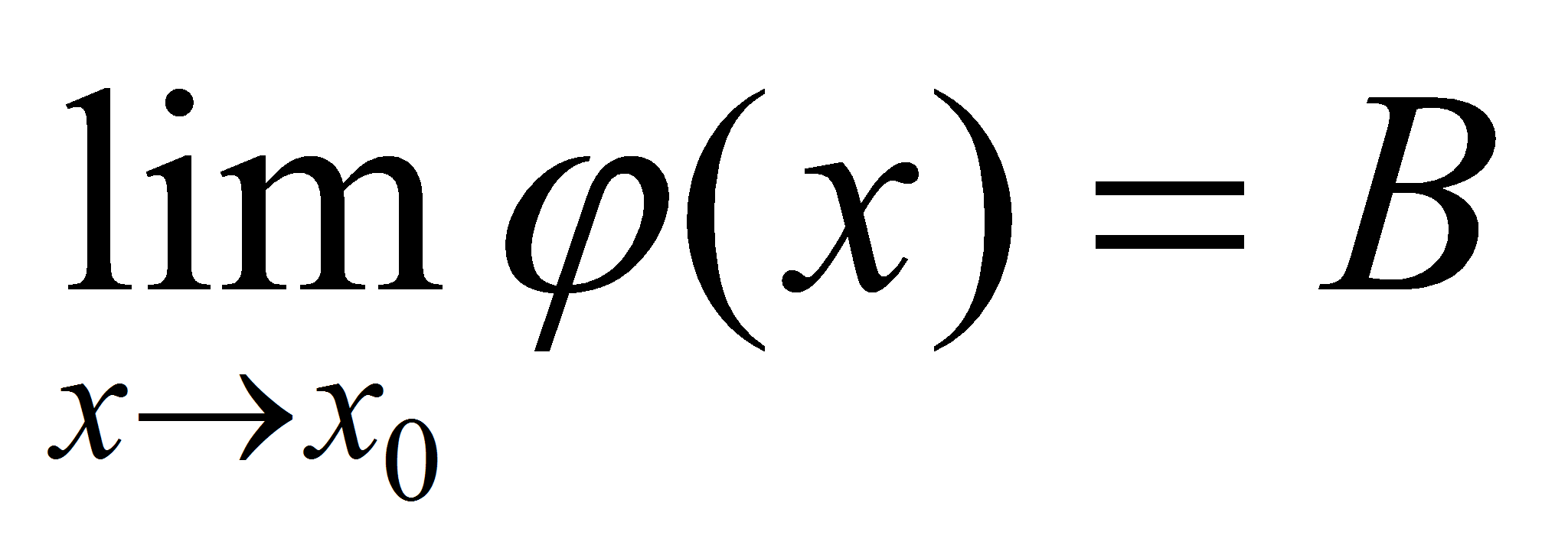 . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать: . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать: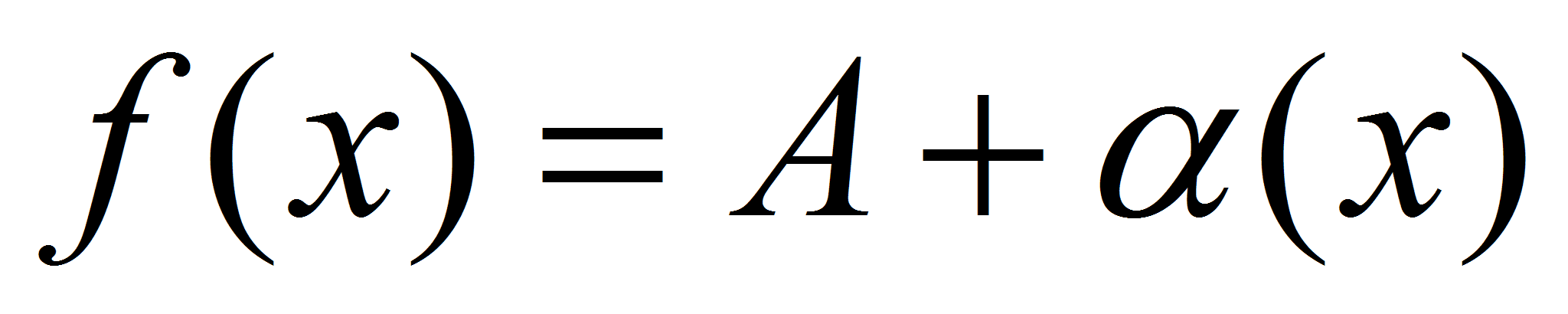 и и 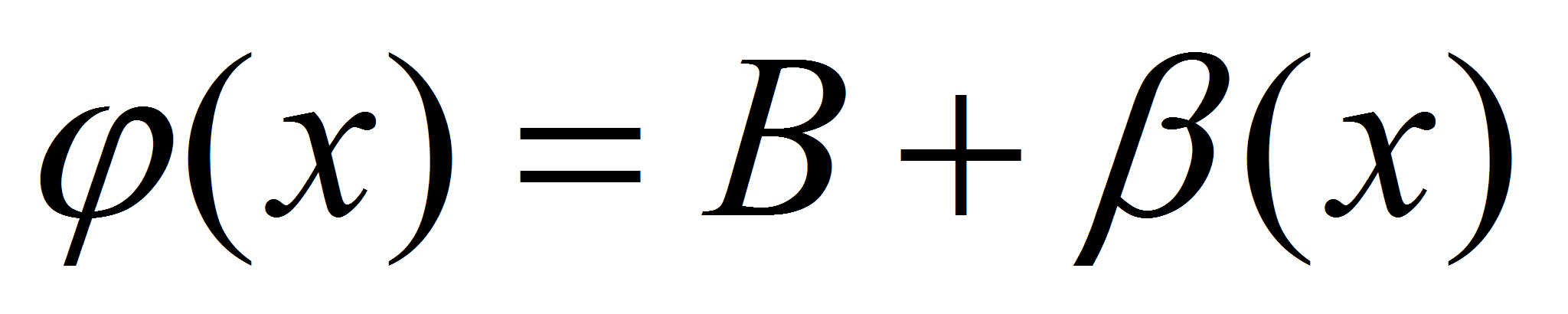 . Следовательно, . Следовательно,  , где , где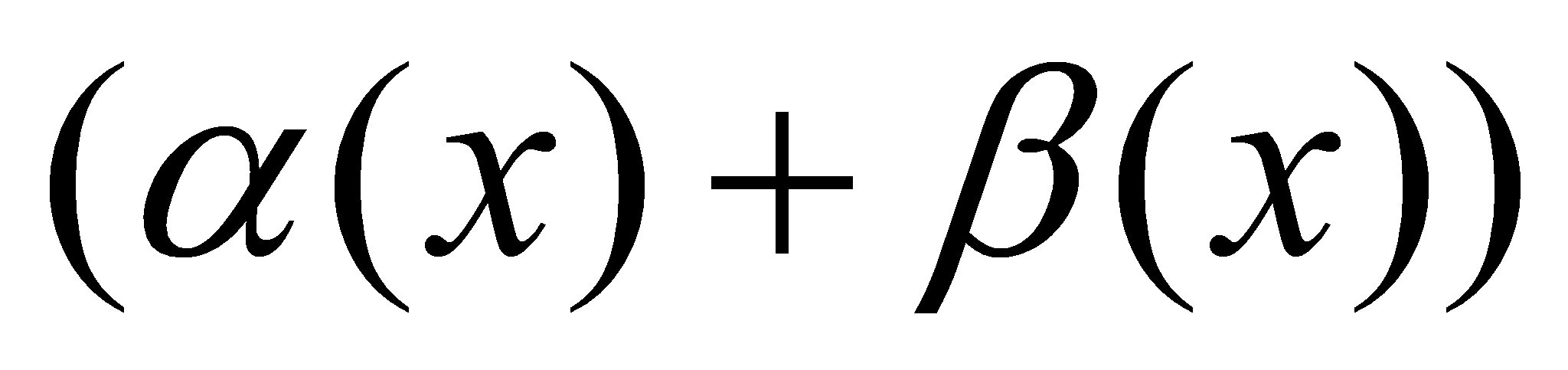 - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать  , или , или 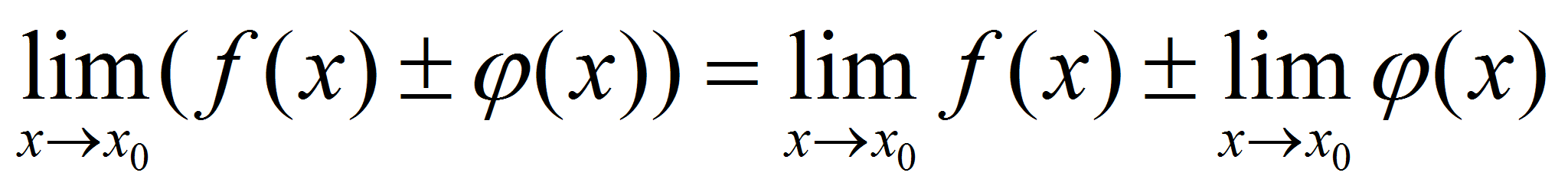 . .
2)Предел произведения двух функций равен произведению их пределов: . .
Доказательство: Пусть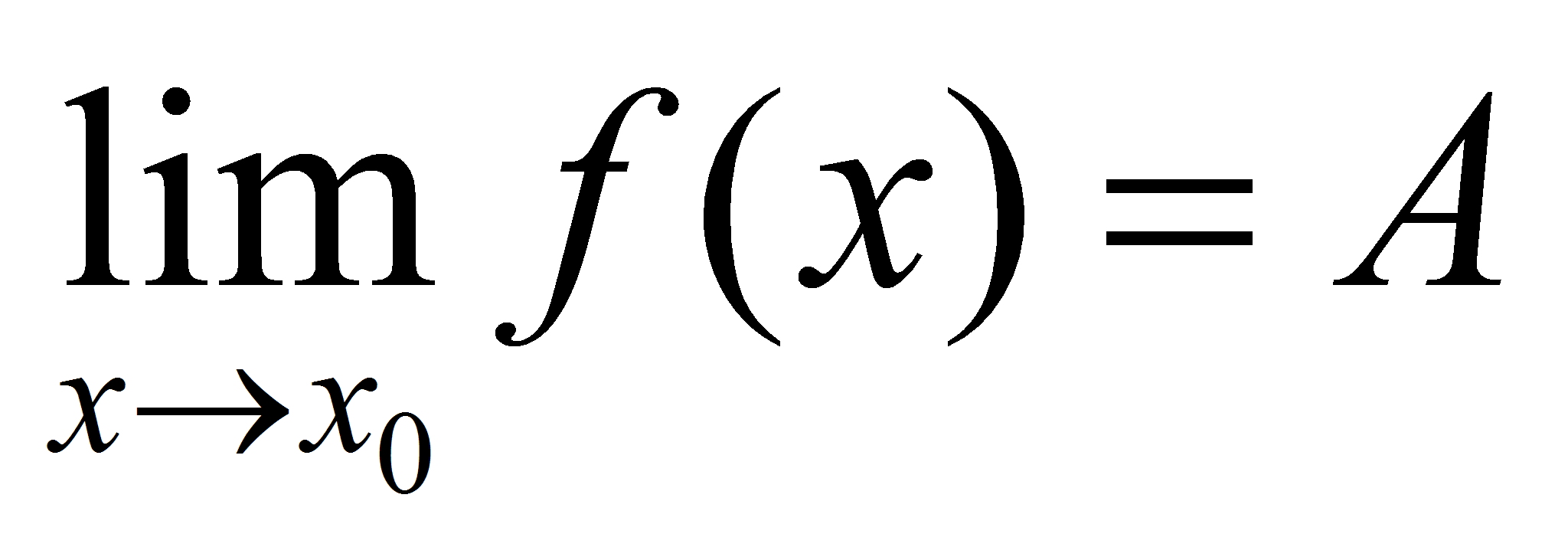 , ,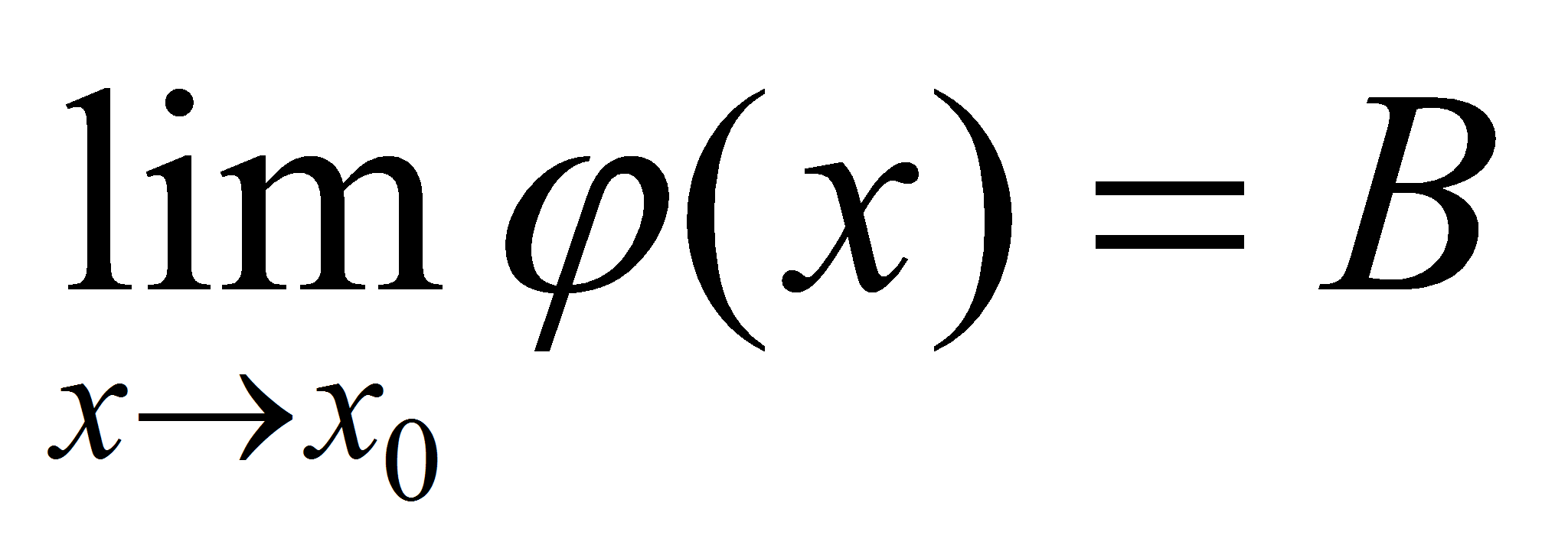 . Тогда . Тогда 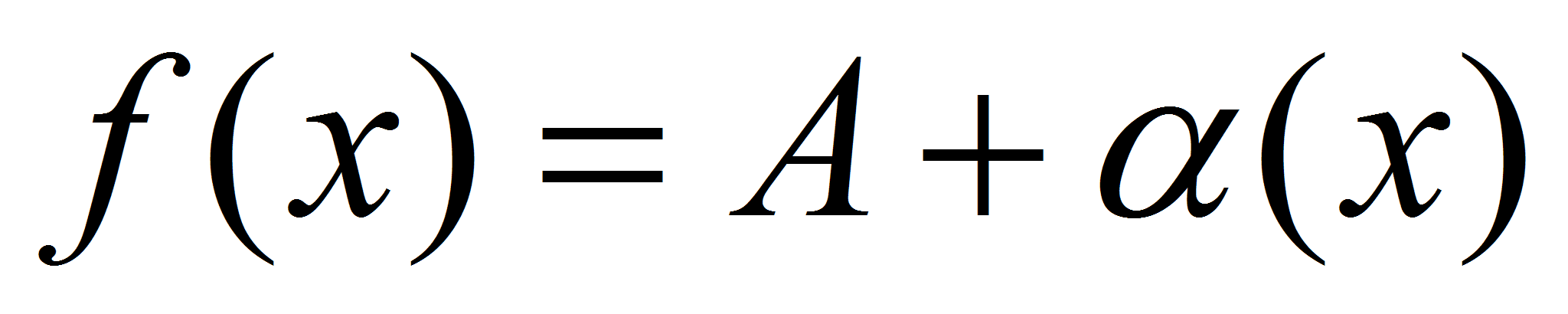 и и 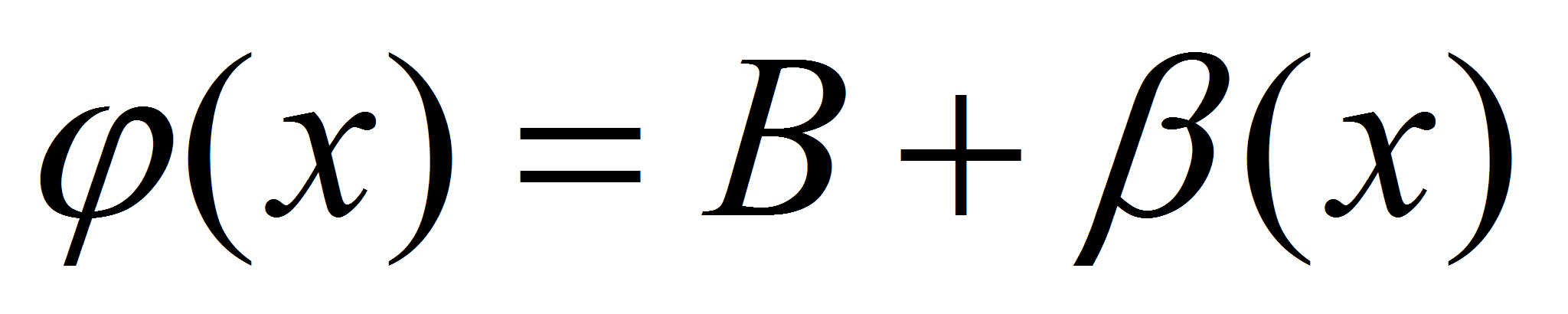 . Следовательно . Следовательно
 , ,  . .
Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда 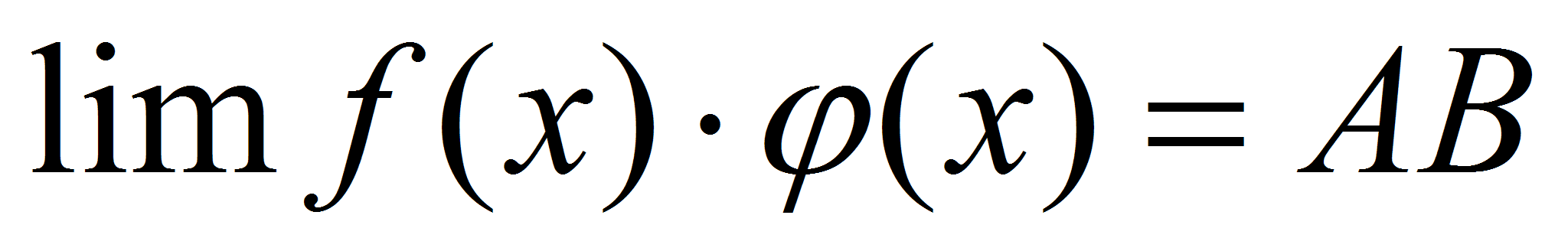 , т.е. , т.е. . .
3)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен: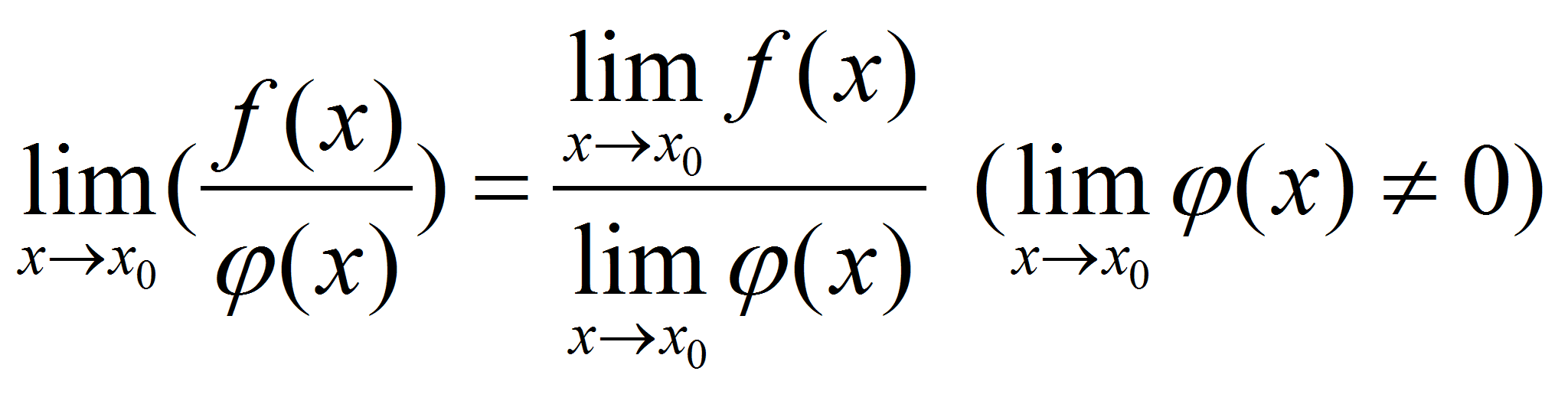 . Доказательство: Пусть . Доказательство: Пусть 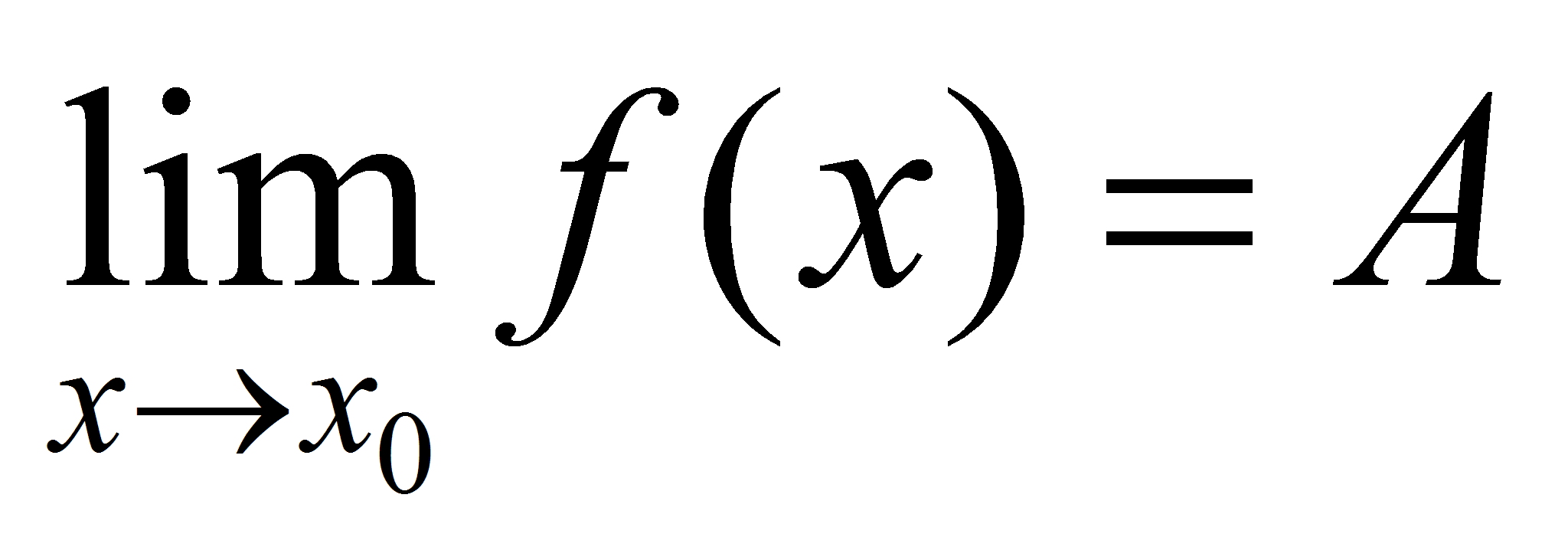 , , . Тогда . Тогда 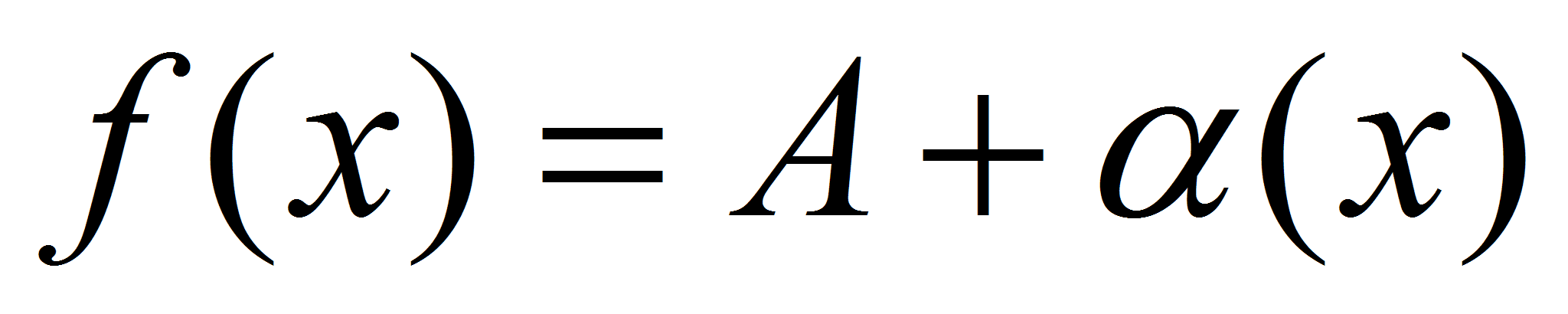 и и 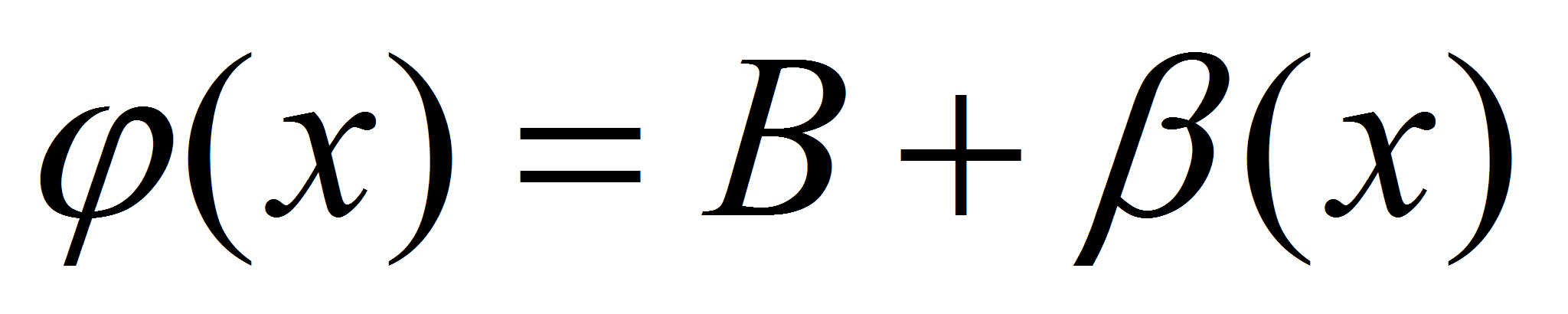 . Тогда . Тогда 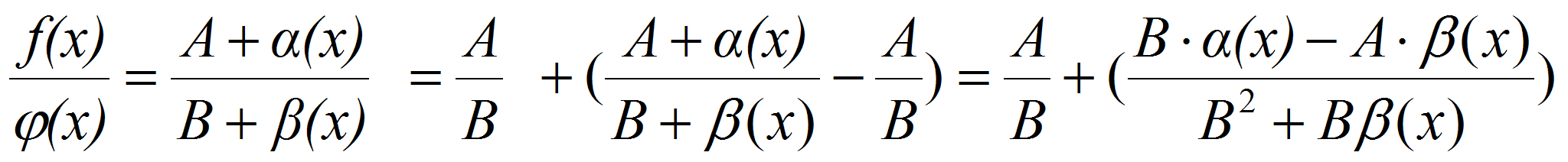 . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция. . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.
Поэтому 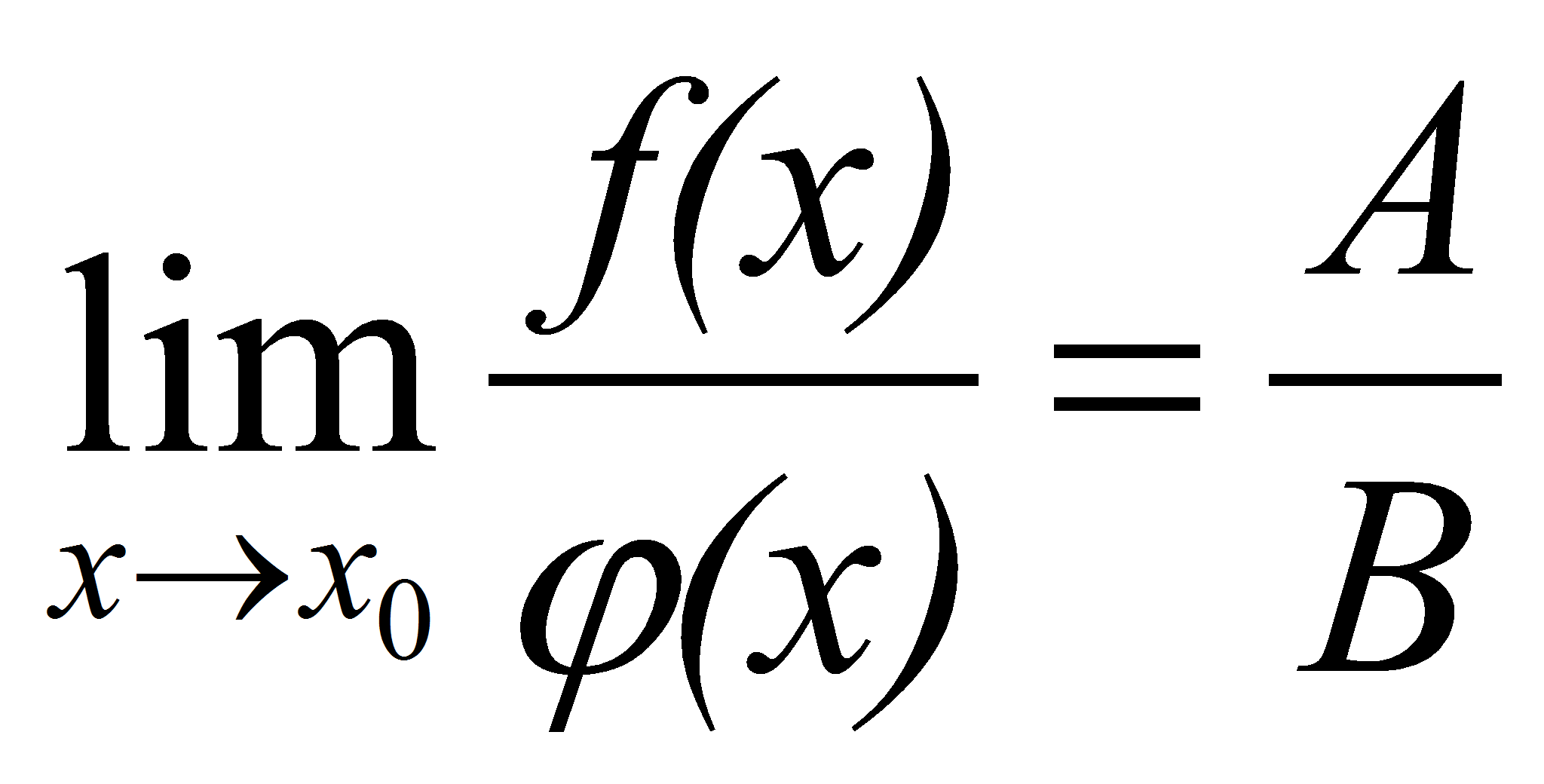 , т.е. , т.е. 
Теорема о пределе сложной функции (с доказательством).


Теорема о знакопостоянстве функции, имеющей ненулевой предел ( с доказательством).
Теорема: Если 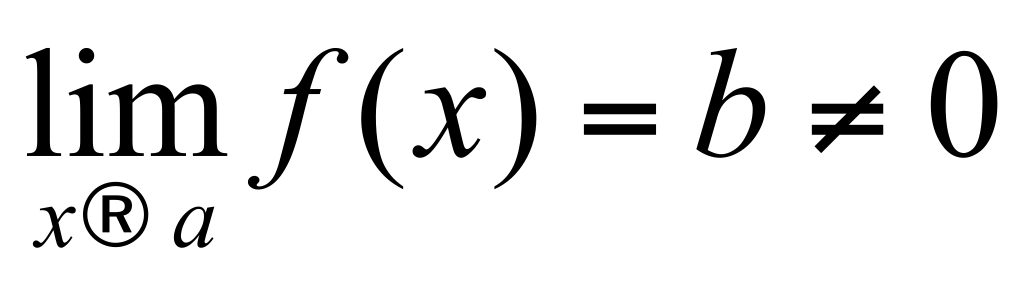 , то существует окрестность точки а, в которой , то существует окрестность точки а, в которой  и знак и знак  совпадает со знаком значения b. совпадает со знаком значения b.
Доказательство: по условию  , т.е. , т.е. , или , или  справедливы неравенства справедливы неравенства  . Возьмём за . Возьмём за  число число  . Тогда . Тогда  , , 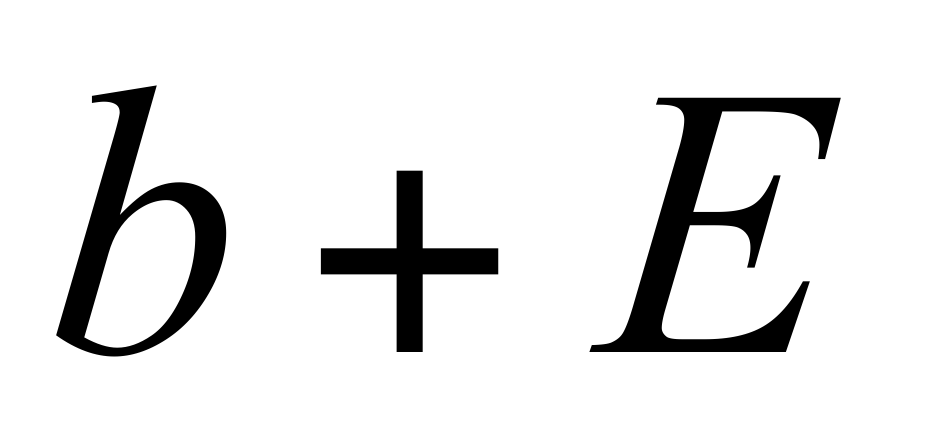 , , 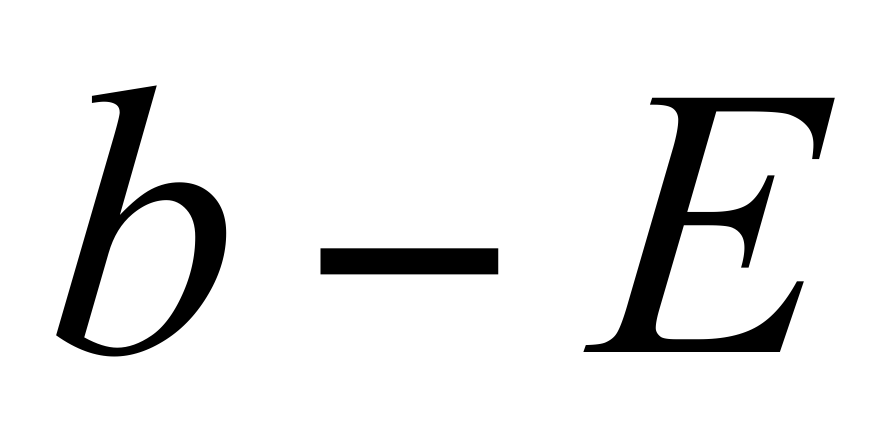 являются числами одного знака. Следовательно, в силу неравенства являются числами одного знака. Следовательно, в силу неравенства 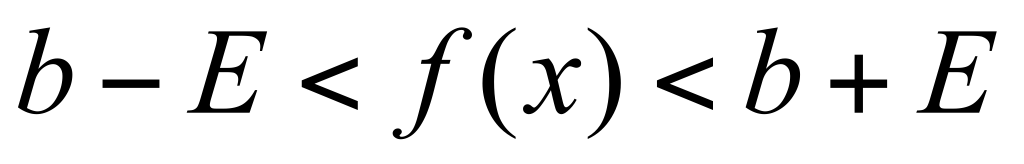 , ,  и имеет знак числа b в указанной и имеет знак числа b в указанной  -окрестности точки а. -окрестности точки а.
Теорема о предельном переходе в неравенстве (доказательство для функции и последовательности).

Теорема о пределе промежуточной функции (доказательство для функции и последовательности).
Теорема Пусть функции 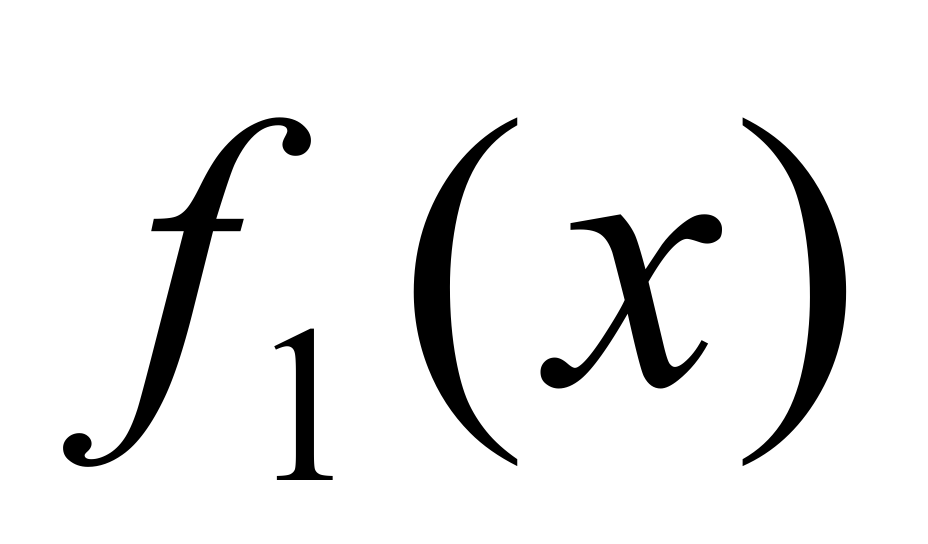 и и 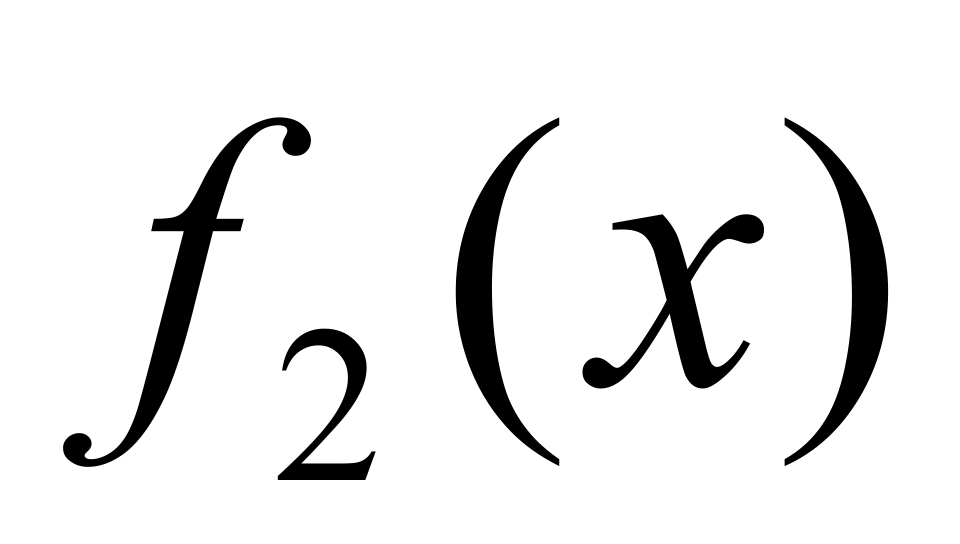 имеет конечный предел А при имеет конечный предел А при  и пусть и пусть 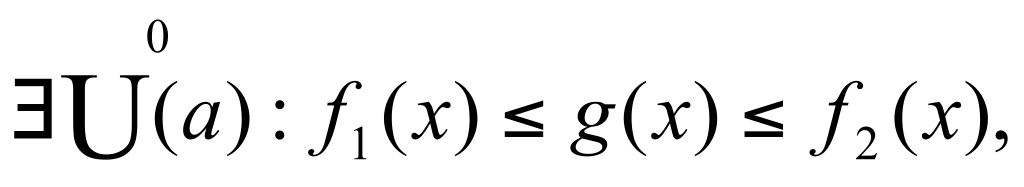 тогда тогда 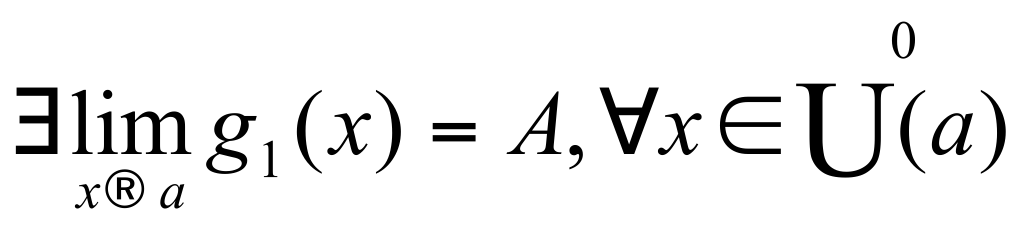 Доказательство: Доказательство:
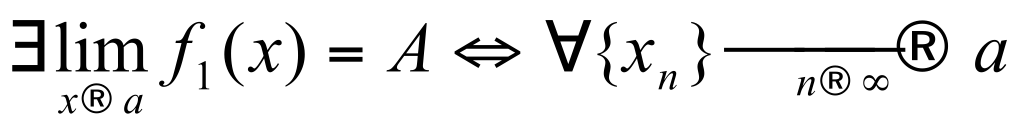 , , 
 , , 
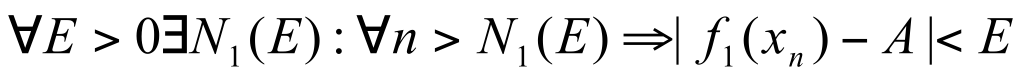 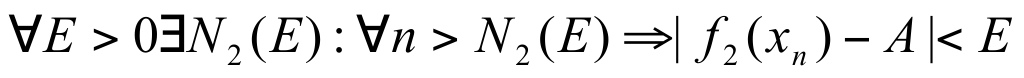
Рассмотрим 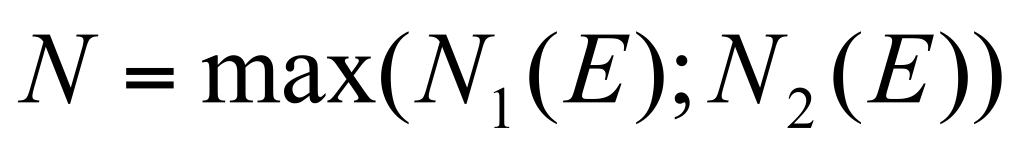 , начиная с некоторого номера N , начиная с некоторого номера N 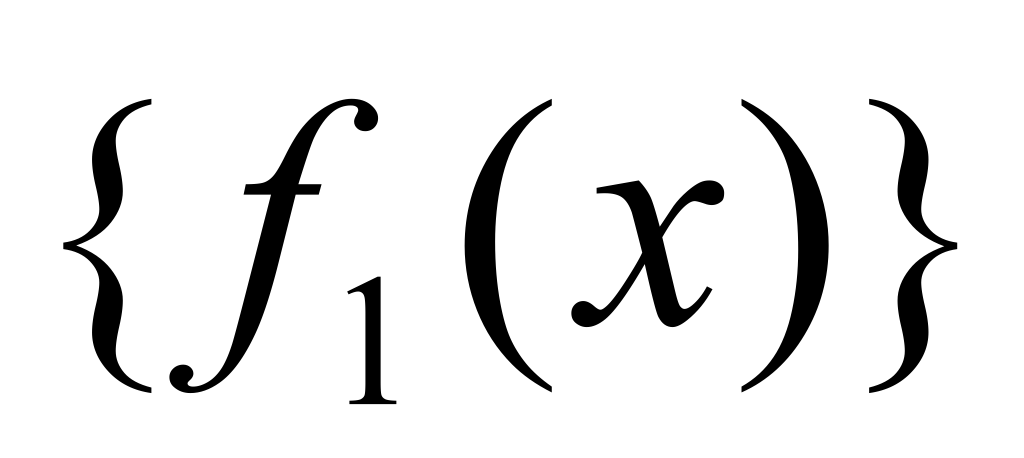 и и  , будут одинакого выполняться , будут одинакого выполняться 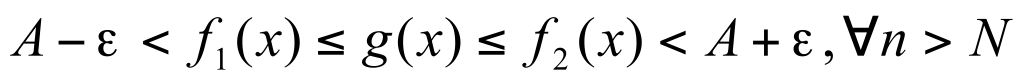 . Значит, . Значит, 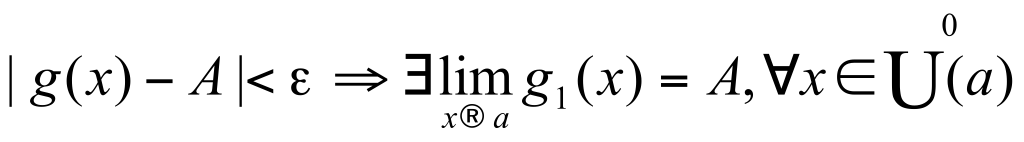
Предел промежуточной последовательности
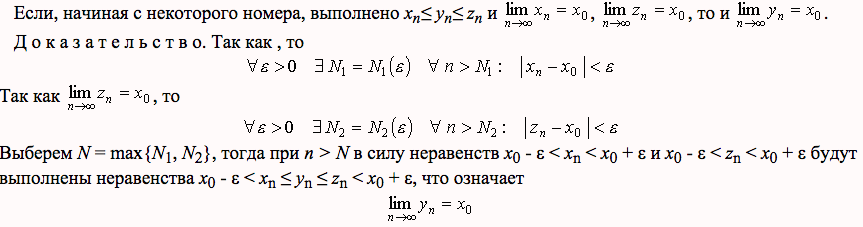
Первый замечательный предел (с выводом). Второй замечательный предел (вывод для функций с использованием теоремы Вейерштрасса для последовательностей).
Вывести 1 замечательный предел: 
Пусть  , , 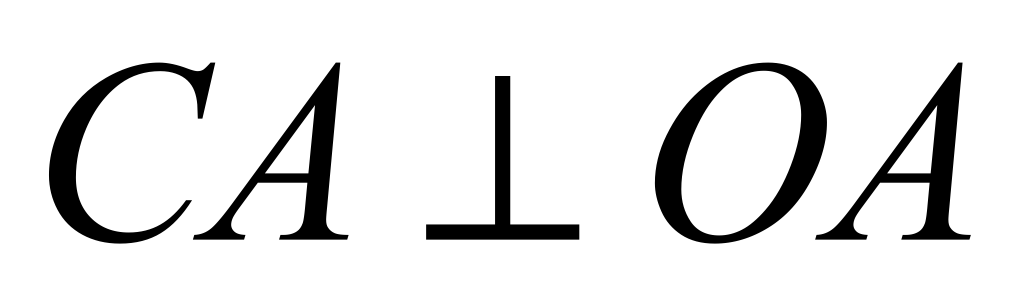 .Проведем геометрическое доказательство, основанное на очевидном соотношении между тремя площадями: Ясно, что .Проведем геометрическое доказательство, основанное на очевидном соотношении между тремя площадями: Ясно, что 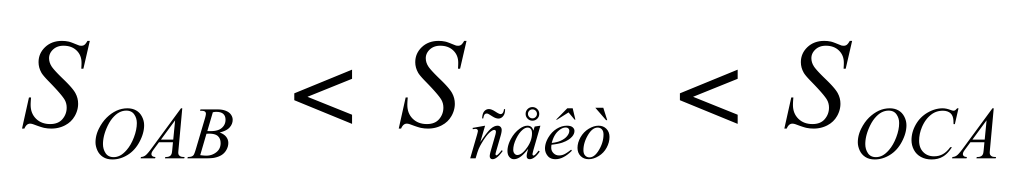 , s2(сектор оab) но , s2(сектор оab) но
 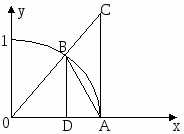
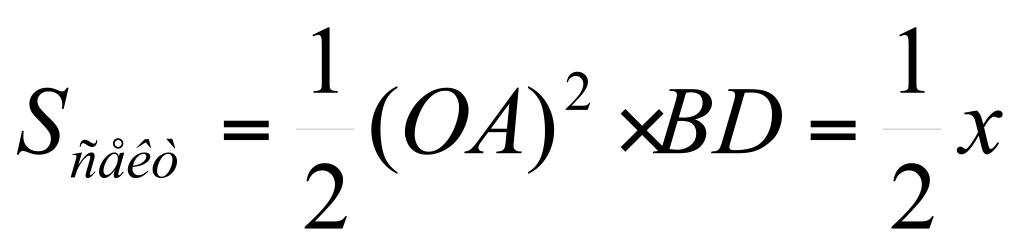
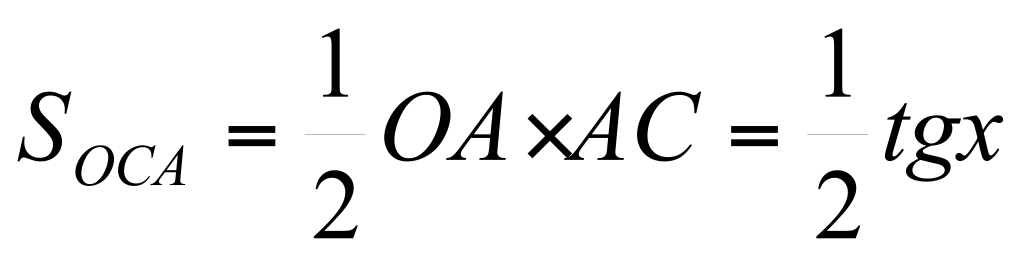 , т.е. , т.е.
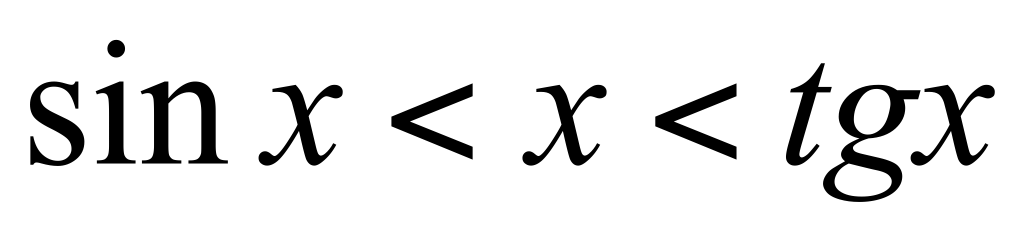 , т.к. , т.к. 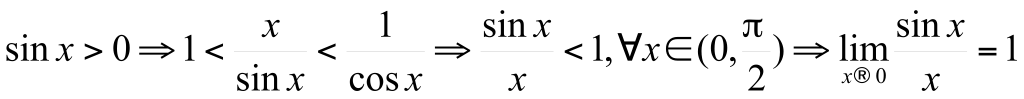 . .
Второй замечательный предел:
Рассмотрим последовательность ,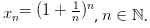 . Покажем, что последовательность ограничена и возрастает. Сначала докажем монотонность. Воспользуемся биномом Ньютона: . Покажем, что последовательность ограничена и возрастает. Сначала докажем монотонность. Воспользуемся биномом Ньютона: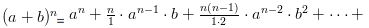 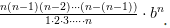 Полагая, что a=1, b= 1/n получим: Полагая, что a=1, b= 1/n получим: 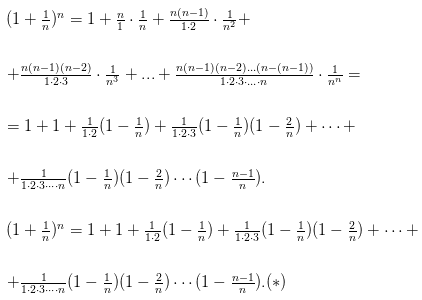 Из равенства (*)следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины , (1-1/n),... возрастают. Поэтому последовательность Из равенства (*)следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины , (1-1/n),... возрастают. Поэтому последовательность  — возрастающая, при этом — возрастающая, при этом  Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (*) на единицу. Правая часть увеличится, получим неравенство: Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (*) на единицу. Правая часть увеличится, получим неравенство: Усилим полученное неравенство, заменив числа 3,4,5...,n, стоящие в знаменателях дробей, числом 2: Усилим полученное неравенство, заменив числа 3,4,5...,n, стоящие в знаменателях дробей, числом 2: 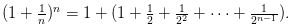 Сумму в скобке найдем по формуле суммы членов геометрической прогрессии: Сумму в скобке найдем по формуле суммы членов геометрической прогрессии: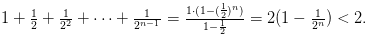 Поэтому: Поэтому:  Итак, последовательность ограничена, при этом для Итак, последовательность ограничена, при этом для  выполняются неравенства (**) и (***) : выполняются неравенства (**) и (***) : 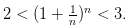 Следовательно, на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой e : Следовательно, на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой e :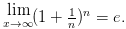 Определение: Числом е называется предел последовательности Определение: Числом е называется предел последовательности т. е. т. е. 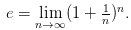
Сравнение бесконечно малых и бесконечно больших функций. Теоремы об эквивалентных бесконечно малых и бесконечно больших функциях(с доказательством). Выделение главной части.
а) Сравнение бесконечно малых функций
Для определения бесконечно малых и бесконечно больших функций воспользуемся, так называемым сравнением функций. Пусть у нас есть две функции p(x) и q(x), которые стремятся к А при аргументе x стремящемся к А. И будем рассматривать предел их отношения при аргументе x, стремящемся к некоторому числу A. Тогда возможны следующие варианты:
1)  , т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)). , т.е. предел отношения функций существует и он равен нулю, в этом случае говорят, что p(x) бесконечно малая функция более высокого порядка и принято обозначать p(x) = o(q(x)).
2)  , т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)). , т.е. предел отношения функций существует и он равен С - некоторой константе, в этом случае говорят, что p(x) и q(x) бесконечно малые функции одного порядка и принято обозначать p(x) = O(q(x)).
3) Если данный предел: 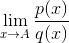 не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы. не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.
4)  , т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)). , т.е. предел отношения функций существует и он равен бесконечности, в этом случае говорят, что g(x) бесконечно малая функция более высокого порядка и принято обозначать q(x) = o(p(x)).
Сравнение бесконечно больших функций Также как и в предыдущем пункте будем рассматривать предел отношения двух функций. Только теперь у нас функции стремятся к бесконечности при аргументе x, стремящемся к А. Возможны следующие варианты:
1)  , т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка. , т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка.
2)  , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка. , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка.
3)  , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка. , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.
4) Если данный предел: 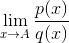 не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы. не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.
 
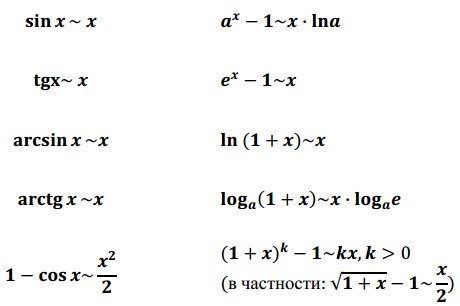
Непрерывность функции действительного переменного в точке. Теорема о непрерывности сложной функции (с доказательством).
Теорема:

Точки разрыва и их классификация. Доказательство непрерывности функции многочлена и y=sin x.
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел и правосторонний предел ;
Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции. называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке (формулировки соответствующей теоремы).
Функцию f(x) называют непрерывной на [a,b], если она непрерывна на (a,b) и непрерывна справа в точке x=a и непрерывна слева в точке x=b.
Первая теорема Вейерштрасса. Если f(x) непрерывна на [a,b], то она ограничена на этом отрезке. 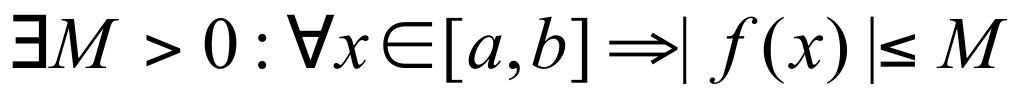 .Вторая теорема Вейерштрасса. Если f(x) непрерывна на [a,b], то она достигает на этом отрезке своего наименьшего (наибольшего) значения. Первая теорема Больцано-Коши. Функция .Вторая теорема Вейерштрасса. Если f(x) непрерывна на [a,b], то она достигает на этом отрезке своего наименьшего (наибольшего) значения. Первая теорема Больцано-Коши. Функция 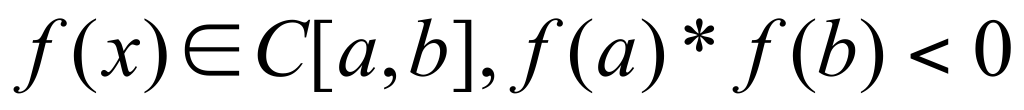 , тогда , тогда 
Доказательство: [a,b] разделим пополам и получим отрезки [a,a+b/2] и [a+b/2,b]. Из них выберем тот, на концах которого ф-ция принимает значения, разные по знаку и обозначим [a1,b1], f(a1)*f(b1)<0. С этим отрезком поступим так же. [a1,a1+b1/2] и [a1+b1/2,b1]. Выберем отрезок с разными по знаку концами. Когда-нибудь получим отрезок  . . 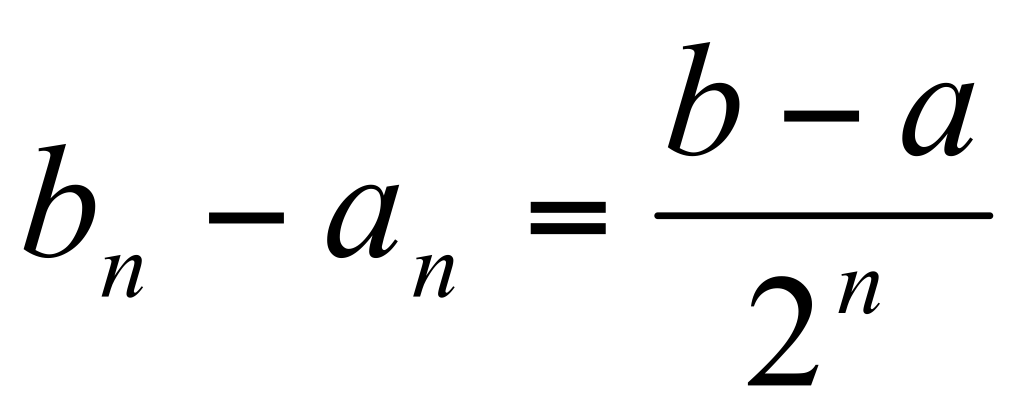 . При . При  , ,  . Получим систему вложенных отрезков . Получим систему вложенных отрезков 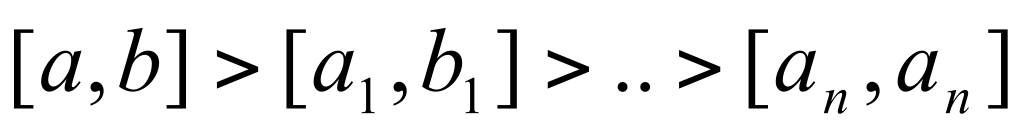 . Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что . Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что  . Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то . Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то 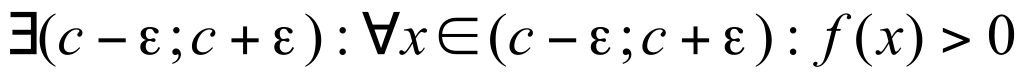 ; ; 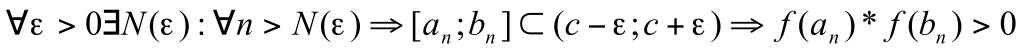 - притиворечие, что и треб. доказ. - притиворечие, что и треб. доказ.
Вторая теорема Больцано-Коши.
Пусть  непрерывна на [a,b] и на концах отрезка принимает значения B и A, ( непрерывна на [a,b] и на концах отрезка принимает значения B и A, ( , тогда для любого числа С: , тогда для любого числа С:  . .
Доказательство. Рассмотрим F(x)=f(x)-C.
F(x) непрерывна на отрезке, как разность двух непрерывных функций.
F(a)*F(b)<0
По первой теореме Б-К 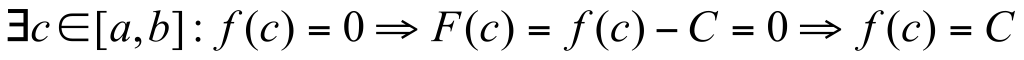 . .
|
 Скачать 3.78 Mb.
Скачать 3.78 Mb.




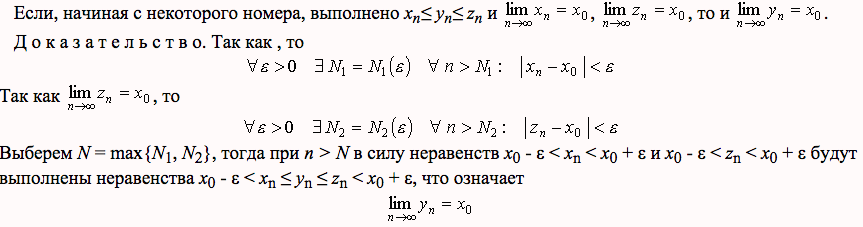

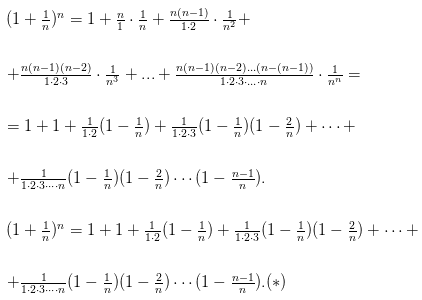 Из равенства (*)следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины , (1-1/n),... возрастают. Поэтому последовательность
Из равенства (*)следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины , (1-1/n),... возрастают. Поэтому последовательность