Транспортная задача. Метод северо-западного угла. Транспортная задача. Метод северозападного угла
 Скачать 227.61 Kb. Скачать 227.61 Kb.
|
1.2 Математическая модельПеременными (неизвестными) транспортной задачи являются xij, i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок по формуле (2). 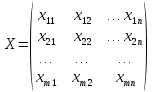 (2) (2)Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны формуле (3). 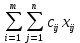 (3) (3)По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид по формуле (4): 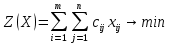 (4) (4)Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид по формуле (5). 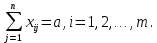 (5) (5)Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид формуле (6). 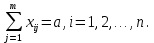 (6) (6)В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей по формуле (7). 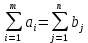 (7) (7)Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи — открытой. Математическая формулировка транспортной задачи такова: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений по формуле (5) и (6)б условиям неотрицательности по формуле (8) и обеспечивающие минимум целевой функции по формуле (4). 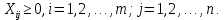 (8) (8)Вывод: цель транспортной деятельности считается достигнутой если найдено оптимально решение. 1.3 Определение опорного плана. Предварительные сведенияОпорный план транспортной задачи находим следующим образом. На каждом шаге в таблице условий задачи заполняем одну клетку, которая называется занятой. Обозначим через Kij клетку, где I -номер пункта отправления (строка), j-номер пункта назначения (столбец). Клетку Kij заполняем так, чтобы удовлетворялись полностью потребности пункта назначения j, либо обеспечивался полный вывоз груза из пункта отправления i. В первом случае временно исключаем из рассмотрения столбец j и изменяем запас груза пункта отправления i. Во втором случае временно исключаем строку i и изменяем потребность груза пункта назначения j. Далее повторяем процедуру с таблицей условий с исключенной строкой или столбцом. В m+n−1-ом шаге получаем задачу с одним пунктом отправления и одним пунктом назначения. Остается свободной одна клетка. Запасы оставшегося пункта отправления будут равны потребностям пункта назначения. Заполнив эту клетку заканчиваем m+n−1-ый шаг и получаем опорный план. Если на некотором шаге (но не на последнем) потребности очередного пункта назначения равны запасам пункта отправления, то временно исключаем из рассмотрения либо столбец, либо строку (только одно из двух). Тогда либо запасы данного пункта отправления, либо потребности данного пункта назначения считаем равным нулю. Этот нуль при очередном шаге записываем в очередную заполняемую клетку. Данный подход обеспечивает ровно m+n−1 занятых клеток, что обеспечивает возможность проверки полученного опорного плана на оптимальность и нахождение оптимального плана. 2 Разбор задачи2.1 Начальные сведенияРешим задачу, даны поставщики с запасами: 14, 66, 33, даны покупатели с потребностями: 53, 35, 73, даны тарифы перевозок единицы груза из каждого пункта отправления во все пункты назначения, они задаются матрицей:
Найти оптимальный план перевозок. |
