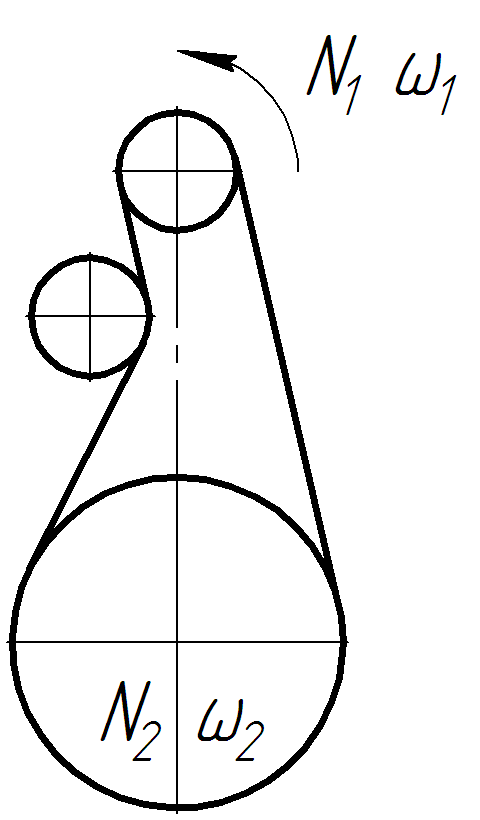
Контрольная работа по деталям машин. Вариант 01. Требуется рассчитать плоскоременную передачу с натяжным роликом (рисунок 1)

• Название: Требуется рассчитать плоскоременную передачу с натяжным роликом (рисунок 1)
• Анкор: Контрольная работа по деталям машин
• Дата: 06.04.2023
• Размер: 416 Kb.
• Имя файла: Вариант 01.doc
• Тип: Документы; #1042120

Задание 1
Требуется рассчитать плоскоременную передачу с натяжным роликом (рисунок 1).

Исходные данные: - мощность на ведущем валу N1 = 8 кВт; - угловая скорость ведущего шкива ω1 = 144 с-1; - угловая скорость ведомого шкива ω2 = 32 с-1. Определяем частоты вращения шкивов (n1 и n2) Определяем передаточное число u' = ω1 / ω2 = 144 / 32 = 4,5

Рисунок 1 – Схема передачи

Определяем предварительный диаметр ведущего шкива
d₁ = (35…70) ∙ δ = (35…70) ∙ 2,8 = 98 … 196 мм
где δ = 2,8 мм – толщина ремня [1, с. 80, таблица 5.1].

Принимаем стандартный диаметр d₁ = 180 мм [1, с. 448, таблица К40].

Определяем предварительный диаметр ведомого шкива
d₂ = u'·d₁(1 – ε) = 4,5·180·(1 – 0,015) = 798 мм
Принимаем стандартный диаметр d₂ = 800 мм [1, с. 448, таблица К40].

Определяем диаметр натяжного ролика
d₀ = d₁ … 0,8 ∙ d₁ = 180 … 0,8 ∙ 180 = 180 … 144 мм
Принимаем стандартный диаметр d₀ = 160 мм [1, с. 448, таблица К40].

Определяем фактическое передаточное число и его отклонение от требуемого (Δu ≤ 3%)

;
Определяем минимальное межосевое расстояние для передачи с натяжным роликом

а ≥ d₁ + d₂ = 180 + 800 = 980 мм
Принимаем межосевое расстояние a = 1135 мм.

Помещать ролик желательно на ведомой ветви так, чтобы угол огибания его ремнем был не более 120°, а центр ролика располагался от центра малого шкива на расстоянии
A ≥ d₀ + (0,5…1) ∙ d₁ = 160 + (0,5…1) ∙ 180 = 250 … 340 мм
Принимаем A = 300 мм.

Для определения точного положения натяжного ролика на ведомой ветви зададимся стандартной длиной ремня = 4000 мм [1, с. 81].

Вычерчиваем схему передачи в масштабе 1:10 (рисунок 2). По вычерченной в масштабе схеме передачи, определяем углы α₁ = 190,8°, α₂ = 228°, α₀ = 58,7° и длины прямолинейных участков λ_1…0 = 247,2 мм, λ_0…2 = 688 мм и λ_2…1 = 1091,8 мм.

Проверяем длину ремня, одновременно уточняя положение натяжного ролика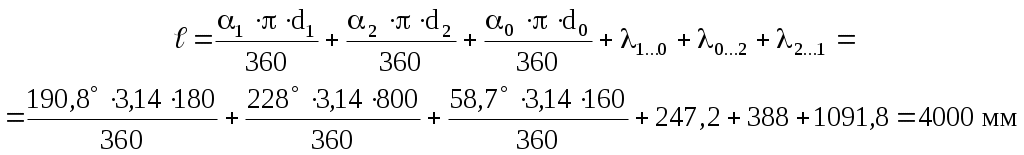

Определяем скорость ремня, сравнивая ее с допускаемой [ ]=35 м/с [1, с. 81]
< 35 м/с
где d₁ = 0,18 м – диаметр ведущего шкива.
Определяем частоту пробегов ремня, сравнивая ее с допускаемой [U]=15 с^-1 [1, с. 82]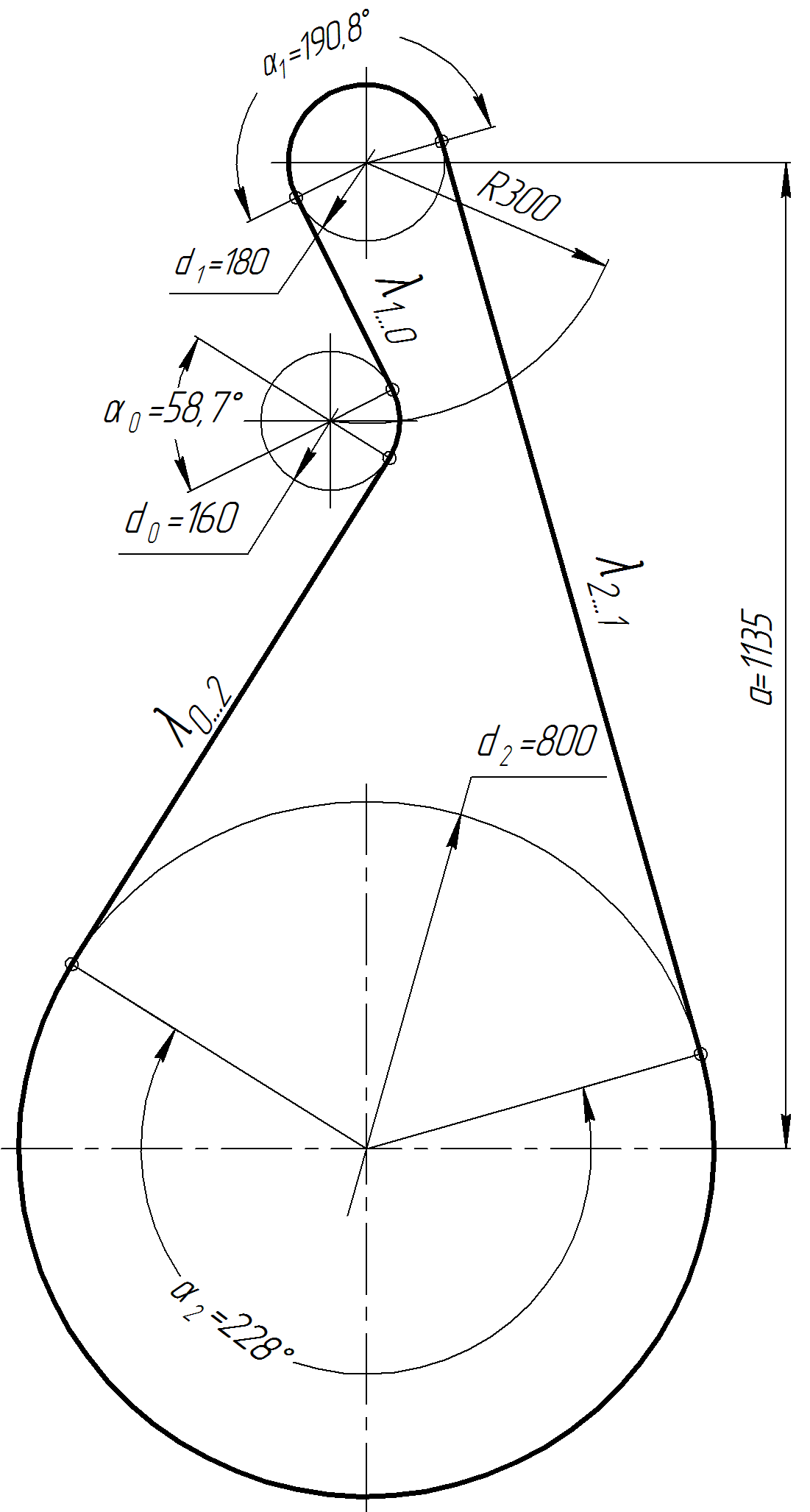
< 15 с^-1

Рисунок 2 – Схема передачи (1:10)
Рассчитываем окружную силу, растягивающую ремни
F_t = N₁ / = 8·10³ / 13 = 615,4 Н
Определяем допускаемую удельную окружную силу
[k_п] = [k₀] ∙ С_θ ∙ С_α ∙ С ∙ С_р ∙ С_d ∙ С_F = 1,6 ∙ 0,8 ∙ 1 ∙ 0,97 ∙ 0,8 ∙ 1,2 ∙ 0,85 = 1,0 МПа
где [k₀] = 1,6 МПа [1, с. 80, таблица 5.1] – допускаемая приведенная удельная окружная сила;

С_θ = 0,8 [1, с. 82, таблица 5.2] – коэффициент от угла наклона линии центров шкивов к горизонту;

С_α = 1 [1, с. 82, таблица 5.2] – коэффициент от угла обхвата ведущего шкива;

С = 0,97 [1, с. 82, таблица 5.2] – коэффициент от центробежной силы;

С_р = 0,8 [1, с. 82, таблица 5.2] – коэффициент от динамичности нагрузки и длительности работы (работа в две смены с умеренными колебаниями нагрузки);

С_d = 1,2 [1, с. 83, таблица 5.2] – коэффициент от диаметра меньшего шкива;

С_F = 0,85 [1, с. 83, таблица 5.2] – коэффициент от неравномерности распределения нагрузки между кордшнурами плоского ремня.

Определяем минимальную ширину ремня

Принимаем хлопчатобумажный цельнотканый пропитанный ремень шириной b=220 мм. Шкивы принимаем шириной 240 мм.

Определяем площадь поперечного сечения ремня
А = δ ∙ b = 2,8 ∙ 220 = 616 мм²
Определяем силу предварительного натяжения ремня
F₀ = A ∙ σ₀ = 616 ∙ 2 = 1232 Н
где σ₀ = 2 МПа [1, с. 80, таблица 5.1] – предварительное натяжение.

Определить силы натяжения ведущей (F₁) и ведомой (F₂) ветвей ремня
F₁ = F₀ + 0,5 ∙ F_t = 1232 + 0,5 ∙ 615,4 = 1540 Н

F₂ = F₀ – 0,5 ∙ F_t = 1232 – 0,5 ∙ 615,4 = 924 Н
Определить силу давления ремня на вал

Рассчитываем напряжение от силы натяжения ведущих ветвей
σ₁ = F₁ / А = 1540 / 616 = 2,5 МПа
Рассчитываем напряжение от изгиба
σ_и = Е_И · δ / D₁ = 100 · 2,8 / 180 = 1,56 МПа

где Е_И = 100 МПа [1, с.123] – условный модуль упругости материала ремня.

Рассчитываем напряжение от центробежной силы
σ = ρ · ² · 10^-6 = 1200 · 13² · 10^-6 = 0,2 МПа
где ρ = 1200 кг/м³ [1, с.123] – плотность материала ремня.

Рассчитываем максимальное напряжение в сечении ремня, сравнивая его с допускаемым [σ]_Р = 8 МПа [1, с. 85]
σ_max = σ₁ + σ_и + σ = 2,5 + 1,56 + 0,2 = 4,3 МПа < 8 МПа

Задание 2
Требуется рассчитать механические передачи привода (рисунок 2).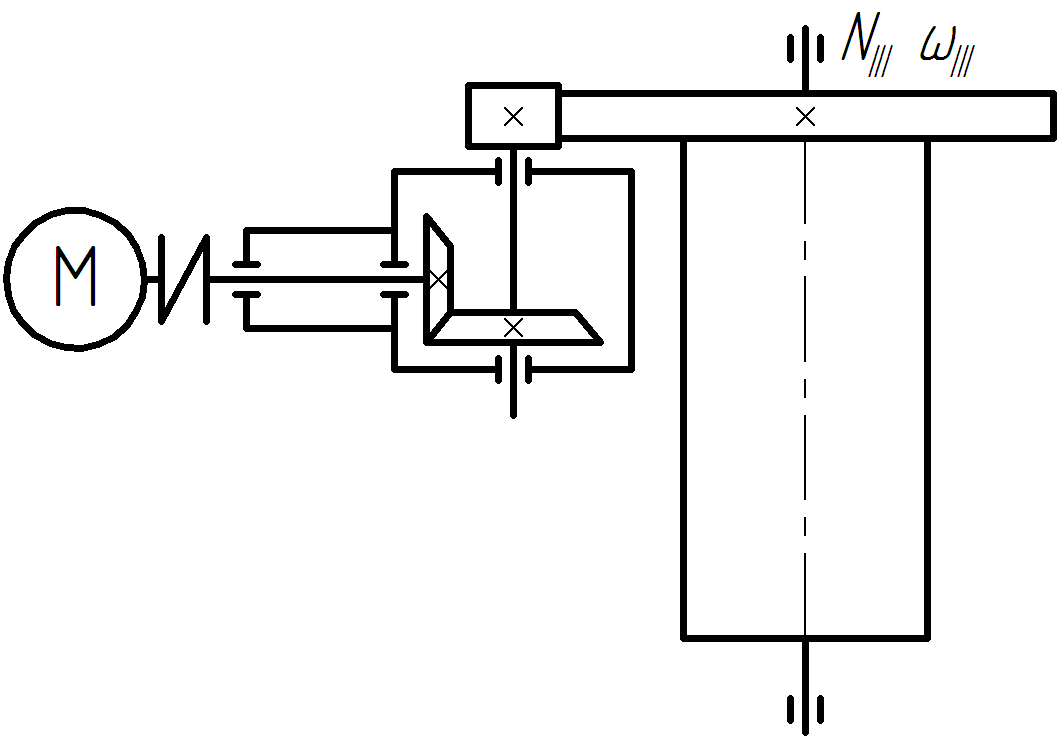

Рисунок 2 – Схема передачи

Исходные данные:

- мощность на ведомом валу N_III = 5 кВт;

- угловая скорость ведомого вала ω_III = 5 с^-1.

- передаточное отношение привода u = 14.
Определяем угловую скорость ведущего вала
ω_I = ω_I ∙ u = 5 ∙ 14 = 70 с^-1;
По кинематической схеме определяем общий КПД привода
η_общ = η_к · η_з · η_м · η^k_пк = 0,97 · 0,97 · 0,98 · 0,99³ = 0,9
где Ση_i – КПД элементов, составляющих привод [1, с. 61, таблица 7]

η_к = 0,97 – КПД конической передачи;

η_з = 0,97 – КПД цилиндрической передачи;

η_м = 0,98 – КПД муфты;

η_п = 0,99 – КПД одной пары подшипников качения.

k = 3 – число пар подшипников качения.

Определяем требуемую мощность электродвигателя
N_Э.тр = N_III / η_общ = 5 / 0,9 = 5,56 кВт

Определяем частоты вращения валов (n₁ и n₃)

Предварительно принимаем передаточное число конической передачи u_к=4,5, тогда передаточное число цилиндрической передачи
u_з = u / u_к = 14 / 4,5 = 3,1
Принимаем u_з = 3,15.
Вычисляем фактическое значение передаточного отношения привода
u = u_к · u_з = 4,5 · 3,15 = 14,175
Определяем отклонение от требуемого (допускается расхождение 5%)

Определяем частоты вращения валов
n_I = n_эд = 668,5 мин^-1

n_II = n_I / u_к = 668,5 / 4,5 = 148,6 мин^-1

n_III = n_II / u_ч = 148,6 / 3,15 = 47,2 мин^-1
Определяем мощности на валах привода
N_III = 5 кВт

N_II = N_III / (η_з · η_п) = 5 / (0,97 · 0,99) = 5,2 кВт

N_I = N_II / (η_к · η_п) = 5,2 / (0,97 · 0,99) = 5,4 кВт
Определяем вращающие моменты на валах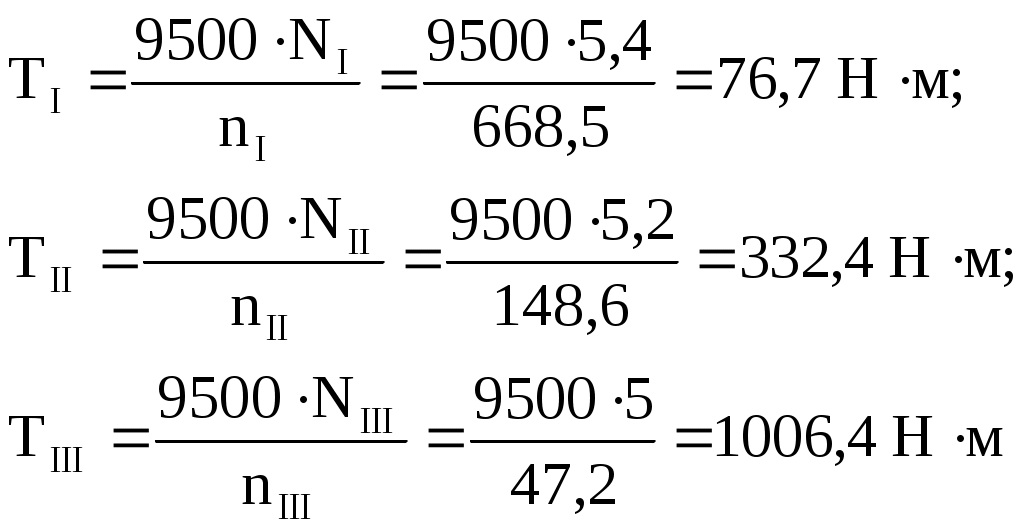

Исходные данные для расчета конической передачи редуктора:

- вращающие моменты Т₁ = 76700 Н·мм

Т₂ = 332400 Н·мм.

- частоты вращения n₁ = 668,5 мин^-1; n₂ = 148,6 мин^-1.

- требуемое передаточное число u = 4,5.

Примем для шестерни и колеса одну и ту же марку стали с различной термообработкой: для шестерни сталь 40Х улучшенную с твердостью НВ 270; для колеса сталь 40Х улучшенную с твердостью НВ 245 [2, с. 34, таблица 3.3].

Определяем допускаемые контактные напряжения:


где σ_Hlimb = 2НВ + 70 = 2245 + 70 = 560 МПа [2, с. 34, таблица 3.2] – предел контактной выносливости материала колеса;

K_HL = 1 [2, с. 33] - коэффициент долговечности при длительной эксплуатации;

[S_H] = 1,1 - коэффициент безопасности [2, с. 33].

Принимаем коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба при консольном расположении шестерни К_Н = 1,35 [2, с. 32, таблица 3.1.].

Принимаем коэффициент ширины венца по отношению к внешнему конусному расстоянию _bRe = 0,285 [2, с. 49].

Определяем внешний делительный диаметр колеса по условию контактной прочности активных поверхностей зубьев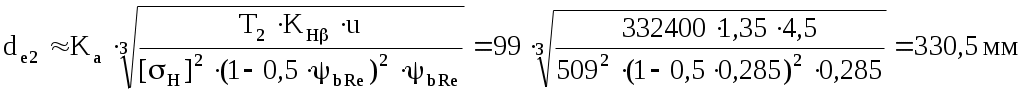

где К_а = 99 [2, с. 49] – коэффициент для прямозубых передач.

Определяем число зубьев колеса, приняв число зубьев шестерни z₁ = 20
z₂ = z₁u = 20  4,5 = 90
Определяем внешний окружной модуль
мм (округляем до 4 мм)
Определяем углы делительных конусов
₂ = аrctg u = аrctg 4,5 = 77°28’;

₁ = 90° – ₂ = 90° – 77°28’ = 12°32’.
Определяем внешнее конусное расстояние R_e и длину зуба b:
мм;

b = _bReR_e = 0,285184,4 = 52,6 мм (принимаем b = 55).
Уточняем внешние делительные диаметры
d_e1 = m_e  z₁ = 4  20 = 80 мм.

d_e2 = m_e  z₂ = 4  90 = 360 мм.
Определяем средний делительный диаметр шестерни и колеса
d₁ = 2 (R_e – 0,5b)  sin₁ = 2 (184,4 – 0,555)  sin12°32’ = 68,1 мм

d₂ = 2 (R_e – 0,5b)  sin₂ = 2 (184,4 – 0,555)  sin77°28’ = 306,32 мм
Определяем внешние диаметры шестерни и колеса (по вершинам зубьев)
d_ae1 = d_e1 + 2m_ecos₁ = 80 + 24cos1232’ = 87,81 мм.

d_ae2 = d_e2 + 2m_ecos₂ = 360 + 24cos7728’ = 361,74 мм.
Определяем средний окружной модуль
мм.
Определяем коэффициент ширины шестерни по среднему диаметру

Определяем среднюю окружную скорость колес
м/с
Назначаем 7-ю степень точности передачи.

Для проверки контактных напряжений уточняем коэффициент нагрузки:
К_Н = К_Н  К_Н  К_НV = 1,3  1,0  1,05 = 1,37
где К_Н = 1,3 [2, с. 39, таблица 3.5] – коэффициент, учитывающий распределение нагрузки по длине зуба при _bd = 0,8, консольном расположении колёс и твёрдости НВ<350;

К_Н = 1,0 [2, с. 39, таблица 3.4] – коэффициент, учитывающий распределение нагрузки между прямыми зубьями;

К_НV = 1,05 [2, с. 40, таблица 3.6] – коэффициент, учитывающий динамическую нагрузку в зацеплении для прямозубых колёс при ≤ 5 м/с.

Проверяем контактное напряжение на активных поверхностях зубьев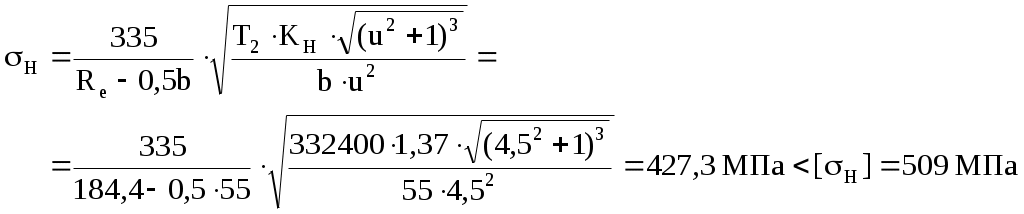

Определяем окружную силу в зацеплении:
Н
Проверяем зубья на выносливость по напряжениям изгиба. Для этого определяем изгибное напряжение по формуле:
;
где K_F = K_F  K_Fv = 1,62  1,3 = 2,1 – коэффициент нагрузки;

K_F = 1,62 [2, с. 43, таблица 3.7] – коэффициент, учитывающий распределение нагрузки по длине зуба при _bd = 0,8, консольном расположении колёс и твёрдости НВ<350;

K_Fv = 1,3 [2, с. 43, таблица 3.8] - коэффициент, учитывающий динамическую нагрузку в зацеплении для прямозубых колёс 7-й степени точности;

= 0,85 [2, с. 51] – опытный коэффициент, учитывающий понижение нагрузочной способности конической прямозубой передачи по сравнению с цилиндрической;

Y_F – коэффициент формы зуба выбираем в зависимости от эквивалентных чисел зубьев:

Рассчитываем эквивалентное число зубьев шестерни и колеса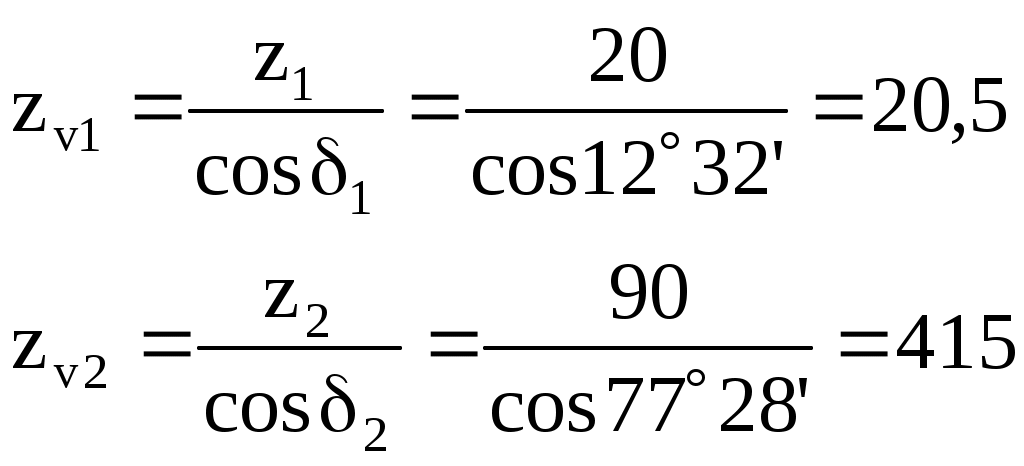

При этом Y_F1 = 4,07 и Y_F2 = 3,6 [2, с. 42.].
Определяем допускаемое напряжение при проверке зубьев на выносливость по напряжениям изгиба по формуле:
;
где = 1,8НВ – предел изгибной выносливости для стали 40Х улучшенной при твердости НВ < 350 [2, с. 44, табл. 3.9];

[S_F] = [S_F]’[S_F]” = 1,75  1 = 1,75 – коэффициент безопасности;

[S_F]’ = 1,75 [2, с. 44, таблица 3.9] для стали 40Х улучшенной при твердости НВ<350;

[S_F]” = 1 [2, стр. 44] – для поковок и штамповок.

Определяем допускаемое напряжение при проверке зубьев на выносливость по напряжениям изгиба для шестерни и для колеса:

- для шестерни

МПа;
где = 1,8НВ = 1,8270 = 486 МПа – предел изгибной выносливости для стали 40Х улучшенной при твердости НВ = 270.
- для колеса

МПа;
где = 1,8НВ = 1,8245 = 441 МПа – предел изгибной выносливости для стали 40Х улучшенной при твердости НВ = 245.

Определяем отношение для шестерни и колеса:

- для шестерни: ;

- для колеса:
Дальнейший расчет ведем для зубьев шестерни, так как полученное отношение для него меньше.

Определяем напряжение для проверки зубьев шестерни на выносливость по напряжениям изгиба

МПа < [_F2] = 277,5 МПа
Радиальная сила для шестерни, равная осевой силе для колеса
F_r1 = F_a2 = F_t  tg  cos₁ = 2253  tg20  cos1232’ = 800 Н
Осевая сила для шестерни, равная радиальной силе для колеса
F_a1 = F_r2 = F_t  tg  sin₁ = 2253  tg20  sin1232’ = 178 Н
Исходные данные для расчета цилиндрической передачи редуктора:

- вращающие моменты Т₁ = 332400 Н·мм

Т₂ = 1006100 Н·мм.

- частоты вращения n₁ = 148,6 мин^-1; n₂ = 47,2 мин^-1.

- требуемое передаточное число u = 3,15.
Примем для шестерни и колеса одну и ту же марку стали с различной термообработкой: для шестерни сталь 40Х улучшенную с твердостью НВ 270; для колеса сталь 40Х улучшенную с твердостью НВ 245 [2, с. 34, таблица 3.3].

Допускаемые контактные напряжения

где σ_Hlimb – предел контактной выносливости при базовом числе циклов.

К_HL = 1,0 – коэффициент долговечности при числе циклов нагружения больше базового, что характерно при длительной эксплуатации редуктора;

[S_H] = 1,2 [2, с. 33] – коэффициент безопасности при улучшении.

Согласно источнику [2, с. 34, таблица 3.2] для легированных сталей с твердостью поверхности зубьев НВ < 350 и термической обработкой (улучшение)
σ_Hlimb = 2 · НВ + 70
Вычислим допускаемые контактные напряжения отдельно для шестерни и колеса

- для шестерни

- для колеса
Для косозубых колес расчетное контактное напряжение вычисляем по формуле
[σ_H] = 0,45·([σ_H1] + [σ_H2]) = 0,45·(508 + 466,5) = 438,5 МПа
Проверяем условие [σ_H] ≤ 1,23·[σ_H2] = 1,23·466,5 = 573 МПа > 438,5 МПа – условие выполнено.

Коэффициент К_Нβ = 1,25 [2, с. 32, таблица 3.1] – для несимметричного расположения колес относительно опор при повышенной твердости зубьев.

Принимаем коэффициент ширины венца по межосевому расстоянию [2, с. 36].

Определим межосевое расстояние из условия контактной выносливости активных поверхностей зубьев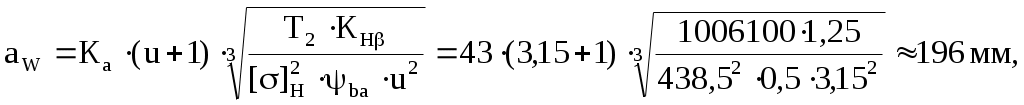

где К_а = 43 [2, с. 32] – коэффициент для косозубых колес;

u = 3,15 – передаточное число цилиндрической ступени редуктора;

T₂ = 1006100 Н·мм – крутящий момент на колесе.

Ближайшее значение межосевого расстояния по ГОСТ 2185-66 a_W = 200 мм [2, с. 36].

Нормальный модуль зацепления принимаем из диапазона
m_n = (0,01…0,02)·a_W = (0,01…0,02)·200 = 2,0 … 4,0 мм (принимаем m_n = 4 мм [2, с. 36].
Определяем необходимое суммарное число зубьев быстроходной ступени предварительно приняв угол наклона зубьев β = 18°

Определяем числа зубьев шестерни и колеса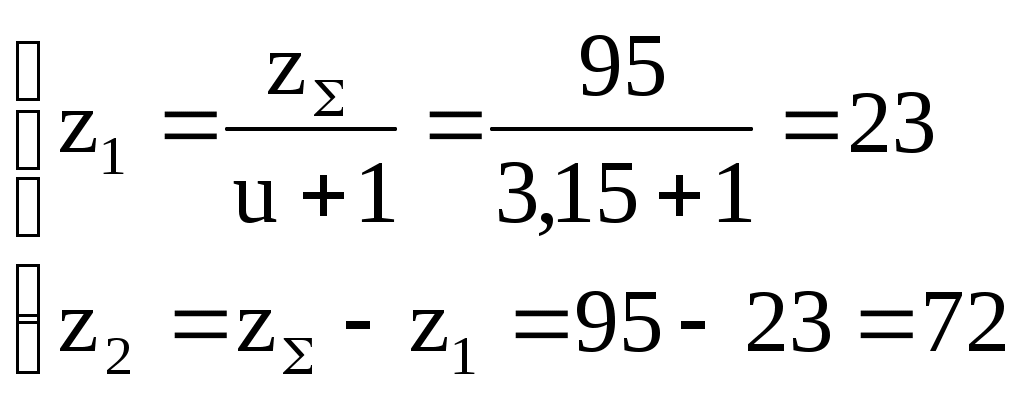

Проверяем межосевое расстояние

Расхождение устраним уточнением угла β

Рассчитываем основные размеры шестерни и колеса

- делительный диаметр шестерни и колеса

мм;

мм.

- диаметр вершин шестерни и колеса

d_а1 = d₁ + 2m = 96,84 + 24 = 104,84 мм;

d_а2 = d₂ + 2m = 303,16 + 24 = 311,16 мм.

- диаметр впадин шестерни и колеса

d_f1 = d₁ – 2,5m = 96,84 – 2,54 = 86,84 мм;

d_f2 = d₂ – 2,5m = 303,16 – 2,54 = 293,16 мм.

Рассчитываем ширину венца колеса b₂ = ψ _ВА · а _W = 0,5 · 200 = 100 мм

Рассчитываем ширину венца шестерни b₁ = b₂ + 5 = 100 + 5 = 105 мм

Определяем коэффициент ширины шестерни по диаметру
ψ_bd = b₁ / d₁ = 105 / 96,84 = 1,1
Определяем окружную скорость колеса
м/с
где n₁ = 148,6 об/мин – частота вращения шестерни (вал II).
При такой окружной скорости назначаем 8-ю степень точности передачи [2, с. 32].

Определяем значение коэффициента неравномерности распределения нагрузки по ширине венца К_Нβ = 1,13 [2, с. 39, таблица 3.5] при ψ_bd = 1,1 и твердости НВ < 350.

Определяем значение коэффициента К_Нα = 1,06 [2, с. 39, таблица 3.4] при 8-й степени точности передачи и < 1 м/с.

Определяем значение динамического коэффициента К_Н = 1 [2, с. 40, таблица 3.6].

Определяем уточненный коэффициент нагрузки
К_Н = К_Нβ · К_Нα · К_Н = 1,13 · 1,06 · 1,0 ≈ 1,2
Проверяем контактные напряжения на активных поверхностях зубьев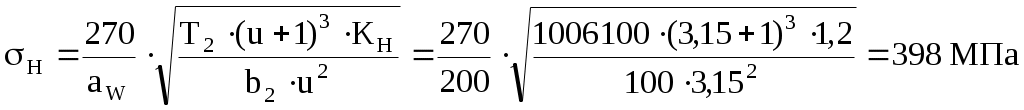
< [σ_H] = 438,5 МПа
Определяем окружное усилие в зацеплении

Определяем радиальное усилие в зацеплении

Определяем осевое усилие в зацеплении

Выполняем расчет зубчатой передачи на изгибную прочность.

Определяем коэффициент нагрузки
K_F = К_Fβ · К_F = 1,27 · 1,1 ≈ 1,4
где К_Fβ = 1,27 [2, с. 43, таблица 3.7] при ψ_bd = 1,1 и твердости НВ < 350;

К_F = 1,1 [2, с. 43, таблица 3.8] при < 3 м/с и 8-й степени точности передачи.

Определяем эквивалентные числа зубьев



Определяем коэффициент формы зуба для шестерни Z_υ1 = 26,8:
Y_F1 = 3,86 [2, с. 42]
Определяем коэффициент формы зуба для колеса Z _υ2 = 84:
Y_F2 = 3,6 [2, с. 42]
Определяем допускаемые напряжения для шестерни и колеса

где = 1,8 ∙ НВ₁ = 1,8 ∙ 270 = 486 МПа [2, с. 44, таблица 3.9] – предел изгибной выносливости шестерни при базовом числе циклов;

= 1,8 ∙ НВ₂ = 1,8 ∙ 245 = 441 МПа [2, с. 44, таблица 3.9] – предел изгибной выносливости колеса при базовом числе циклов;

[S_F] = [S_F]´ · [S_F]´´ = 1,8 · 1 = 1,8 – коэффициент безопасности;

[S_F]´ = 1,8 [2, с. 44, таблица 3.9] – коэффициент, учитывающий свойства материалов и термообработку;

[S_F]´´ = 1 [2, с. 44] – для поковок и штамповок.

Производим сравнительную оценку прочности на изгиб зубьев шестерни и колеса:

- для шестерни

[_F1]/ Y_F1 = 270 / 3,86 = 70

- для колеса

[_F2]/ Y_F2 = 245 / 3,6 = 68

Расчет показывает, что [_F1]/ Y_F1 > [_F2]/ Y_F2 , следовательно, зубья колеса менее прочные, поэтому дальнейший расчет ведем по зубьям колеса.

Определяем коэффициент, учитывающий угол наклона зуба



Определяем коэффициент торцевого перекрытия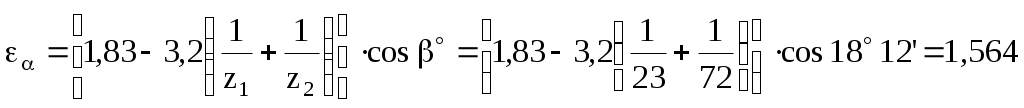



Определяем фактическое напряжение изгиба в опасном сечении зуба

МПа
где b₂ = 100 мм – ширина венца колеса.

Из проверочного расчета видно, что фактическое изгибное напряжение не превышает допускаемое: _F = 48,1 МПа < []_F2 = 245 МПа.

Список использованных источников
1 Шейнблит, А. Е. Курсовое проектирование деталей машин. М.: Высш. шк., 1991. – 432 с.

2 Чернавский, С. А. Курсовое проектирование деталей машин. М.: Машиностроение, 1988 – 416 с.