Требуется выбрать и дать техническое и экономическое
 Скачать 216.11 Kb.
|
 Наименьшая среди четных загрузок (отмеченных знаком минус) равна 20 (в клетке А2Б1). Уменьшив на 20 загрузки клеток А1Б3, А2Б1 и А3Б2 и увеличив также на 20 загрузки клеток А3Б3, A1B1 и А2Б2, получим новый план, представленный в табл. 11. По этому варианту плана транспортная работа составит 1700 тонно-километров, или на 60 тонно-километров меньше.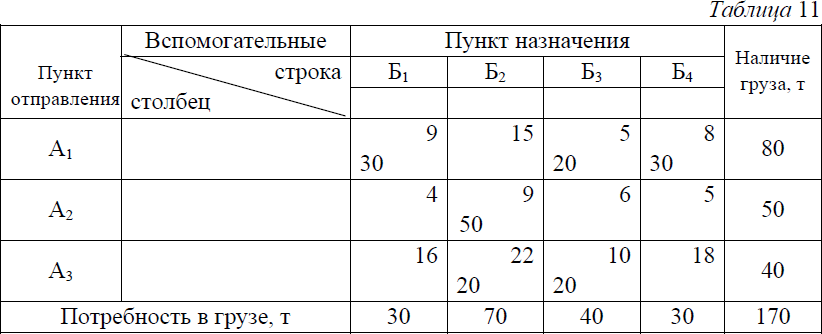 Полученный план лучше предыдущего, однако, неизвестно, является ли он оптимальным. Чтобы ответить на этот вопрос, необходимо исследовать его на оптимальность, повторив весь процесс вычислений. Из табл. 11 видно, что и этот план, как и предыдущий, не является оптимальным. Об этом говорит наличие в матрице потенциальной клетки A1Б2. Изменив уже известным способом загрузки в клетках, отмеченных вершинами вновь построенной цепочки, получаем новый план, представленный в табл.12 . Для его проверки на оптимальность приступаем к расчету индексов и убеждаемся, что все их определить не удается. Причиной этого является так называемое вырождение плана, т.е. уменьшение числа занятых клеток против необходимого.  Дело в том, что все индексы могут быть найдены, и притом однозначно, только при строго определенном количестве занятых клеток, равном в общем случае m+n—1, где m—число пунктов отправления, n—число пунктов назначения. В нашей задаче m=3, а n=4. Следовательно, для определения всех индексов нужно иметь в матрице 3+4—1=6 занятых клеток. В табл. их только пять, поэтому индексы U3 V3 не удается определить. 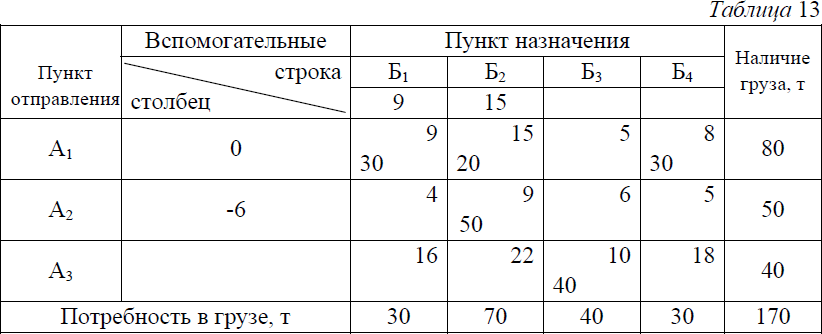 Вырождение матрицы так же, как и излишнее количество занятых клеток, нарушают нормальную процедуру вычислений и их нужно устранять. Избавиться от вырождения можно путем записи в одной из незанятых клеток матрицы перевозки объемом 0 тонн. В табл. 13 нулевую загрузку можно поставить в одну из клеток A1Б3, А2Б3, А3Б1 А3Б2 и А3Б4. Легко проверить, что только эти клетки, став занятыми нулевой загрузкой, позволят найти недостающие индексы U3 и V3. Лучше всего поставить нулевую перевозку в клетку с меньшим расстоянием, т.е. в клетку А1Б3. Теперь определив недостающие индексы, убеждаемся, что последний план является оптимальным, поскольку у всех незанятых клеток матрицы расстояния больше суммы соответствующих им индексов (табл. 14). Транспортная работа по этому плану составит 1600 тонно- километров. 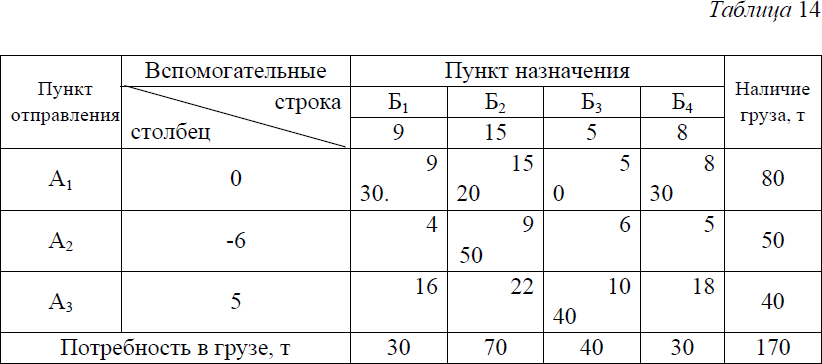 В случае если число занятых клеток в матрице больше, чем m+n—1, поступают следующим образом. В табл. 15 - семь занятых клеток вместо необходимых шести (m+n-1=3+4—1=6). Наличие лишней занятой клетки приводит к тому, что индексы определяются неоднозначно. В первом случае U2=9—15= - 6, во втором U2=6—5= 1. 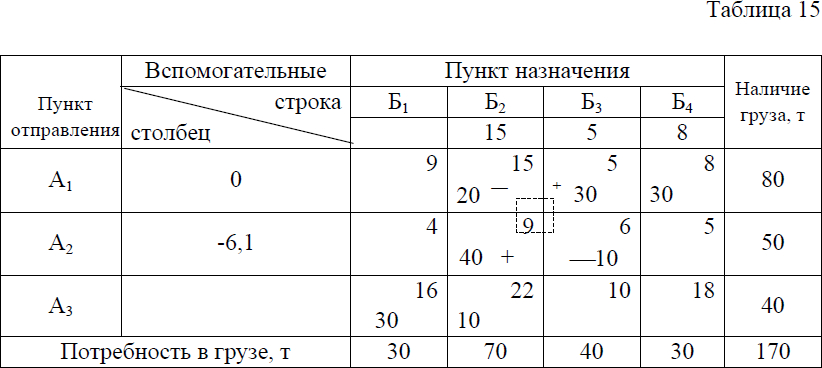 Уменьшение числа занятых клеток производится следующим образом. В матрице строят замкнутую цепочку из горизонтальных и вертикальных отрезков так, чтобы все ее вершины находились в занятых клетках (см. табл. 16). Такая цепочка в матрице с числом занятых клеток более m+n -1 всегда имеется. На вершинах цепочки, начиная с клетки, имеющей наименьшую загрузку, расставляют попеременно знаки минус и плюс, после чего загрузки со знаком минус уменьшают, а со знаком плюс увеличивают на величину наименьшей из них. В результате число занятых клеток уменьшится не менее чем на одну (табл.17). При необходимости данную процедуру повторяют столько раз, сколько это необходимо для получения m+n -1 занятых клеток. 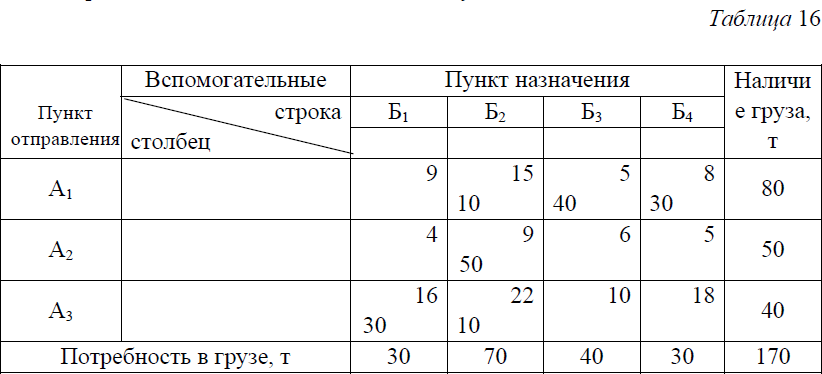 |