Задача по электротехнике. Задача 1. Требуется выполнить
 Скачать 312.07 Kb. Скачать 312.07 Kb.
|
|
вариант 49 Задание 1 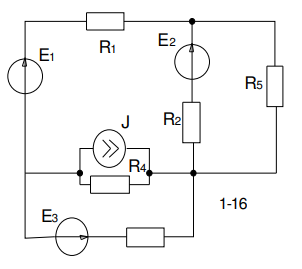  Расчет линейной электрической цепи постоянного тока. Дана электрическая цепь, содержащая источники постоянной ЭДС и постоянного тока. Номер схемы и параметры элементов заданы в таблице 1. Схемы приведены на рис.1. Требуется выполнить: 1. Записать систему уравнения по законам Кирхгофа для расчета токов в цепи. 2. Рассчитать токи в ветвях цепи методом контурных токов. 3. Рассчитать токи в ветвях цепи методом узловых потенциалов. 4. Определить мощность потребителей и источников и проверить баланс мощности.  1. Записать систему уравнения по законам Кирхгофа для расчета токов в цепи.  Составим уравнения по первому закону Кирхгофа. При составлении уравнений "втекающие" в узел токи будем брать со знаком "+", а "вытекающие" - со знаком "-". Количество уравнений, составляемых по первому закону Кирхгофа, равно Nу−1, где Nу - число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 3 - 1 = 2.  Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Количество уравнений, составляемых по второму закону Кирхгофа, равно Nв−Nу+1, где Nв - число ветвей без источников тока. Для данной схемы количество уравнений по второму закону Кирхгофа равно 5 - 3 + 1 = 3.  Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:  Подставим в полученную систему уравнений значения сопротивлений и источников и получим: 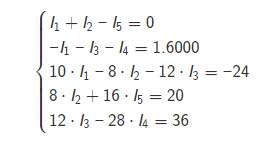 Решим систему уравнений и получим искомые токи: 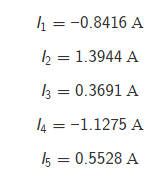 2. Рассчитать токи в ветвях цепи методом контурных токов. Рассчитаем схему по методу контурных токов. В данной схеме: узлов - 3, ветвей без источников тока - 5, независимых контуров - 3. Количество уравнений, составляемых по методу контурных токов, равно Nв−Nу+1, где Nв - число ветвей без источников тока, Nу - число узлов. Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 5 - 3 + 1 = 3. Произвольно зададим направления обхода контуров и соответствующие контурные токи. Принятые направления обхода контуров: Контур №1 обходится через элементы E1, R1, E2, R2, R3, E3 в указанном порядке. Через эти элементы протекает контурный ток I11. Контур №2 обходится через элементы R2, E2, R5 в указанном порядке. Через эти элементы протекает контурный ток I22. Контур №3 обходится через элементы E3, R3, R4 в указанном порядке. Через эти элементы протекает контурный ток I33. Дополнительно зададим контурные токи, создаваемые источниками тока. Контурный ток J протекает через элементы J, R3, E3 в указанном порядке. Составим уравнения по методу контурных токов. 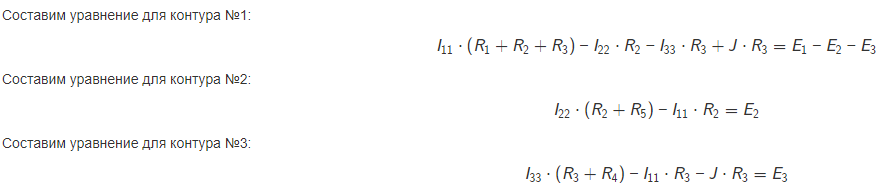 Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:  Подставим в полученную систему уравнений значения сопротивлений и источников и получим: 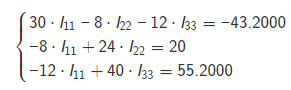 Решим систему уравнений и получим искомые контурные токи: 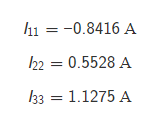  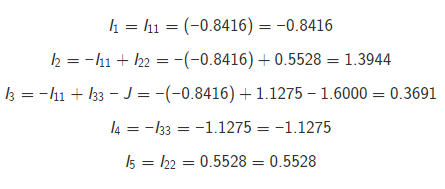 3. Рассчитать токи в ветвях цепи методом узловых потенциалов. Рассчитаем схему по методу узловых потенциалов. В данной схеме: узлов - 3, ветвей - 6, из них особых ветвей - 0. Под особыми ветвями понимаются ветви, в которых имеется только источники ЭДС. Количество уравнений, составляемых по методу узловых потенциалов, равно Nу−1−Ne, где Nу - число узлов, Ne - число особых ветвей. Для данной схемы количество уравнений, составляемых по методу узловых потенциалов, равно 3 - 1 - 0 = 2. В исходной схеме нет особых ветвей. Примем потенциал узла №1 равным нулю, т.е.φ1=0 В 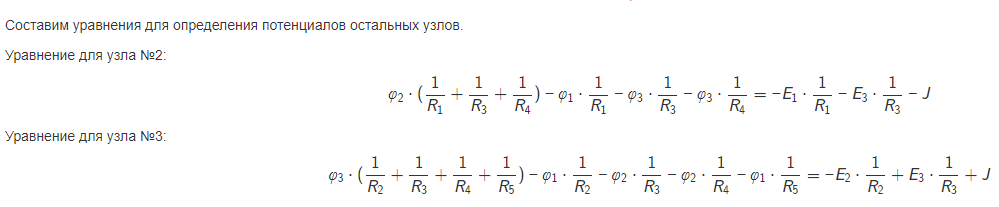    Проверим баланс мощностей. Определим мощность, потребляемую приёмниками: Подставим числовые значения и получим: Определим мощность, отдаваемую источниками: Sист=SE+SJ, где SE - мощность, отдаваемая источниками ЭДС, SJ - мощность, отдаваемая источниками тока. Определим мощность SE, отдаваемую источниками ЭДС: Подставим числовые значения и получим:  Определим мощность SJ, отдаваемую источником тока J: Определим напряжение на источнике тока J, обозначенное как UJ. Для этого рассмотрим контур, проходящий через элементы J, R3, E3 в указанном порядке, и составим для этого контура уравнение по второму закону Кирхгофа. Получим: Выразим из полученного уравнения напряжение UJ и подставим числовые значения. Получим:  |
