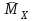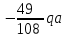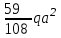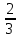Статически неопредлимые системы. Задача 2. Для заданной схемы нагружения (Приложение 9) раскрыть статическую неопределимость и построить эпюры внутренних усилий
 Скачать 280.56 Kb. Скачать 280.56 Kb.
|
|
Расчет статически неопределимых систем Задача №2. Для заданной схемы нагружения (Приложение 9) раскрыть статическую неопределимость и построить эпюры внутренних усилий.  Исходные данные q = 13 Н/мм a = 450 мм Е = 2∙105 МПа [δ] = 20 мм [σ] = 135 МПа с = 1 1. Вычерчиваем в масштабе схему нагружения  2. Определяем количество неизвестных реакций в опорах и количество уравнений равновесия. В данной задаче четыре неизвестные реакции – три в жесткой заделке и одна в шарнирно-подвижной опоре. Уравнений равновесия три – так как система плоская. Степень статической неопределимости – это разность между количеством неизвестных реакций в опорах и количеством уравнений равновесия: 4 неизвестные реакции – 3 уравнения равновесия = 1 раз статически неопределимая система (4 н.р. – 3 ур.р. = 1 р.с.н.с.). Степень статической неопределимости показывает число дополнительных (лишних) связей. 3. Выбираем основную систему (О.С.). Это система без нагрузок и дополнительных связей – конструкция с необходимой опорой (без лишней опоры) – жесткой заделки достаточно для равновесия системы, но при этом может быть большое перемещение под нагрузкой свободного конца конструкции, чтобы его не было ставят дополнительную опору. В итоге перемещения нет, но данная опора дополнительная (лишняя). В заданной схеме оставляем жесткую заделку и убираем шарнирно-подвижную опору.  4. В том месте, где убрали опору прикладываем силу неизвестную Х1 и прикладываем всю внешнюю нагрузку. Система со всей внешней нагрузкой и неизвестной силой в том месте, где была опора – эквивалентная.  5. Записываем канонические уравнения. Условие, при котором в направлении отброшенной реакции опоры не будет перемещений - каноническое уравнение: то есть в нашем варианте не должно быть вертикального перемещения.  где Δ1F - перемещение грузового состояния, δ11 - перемещение единичного состояния. Из данного условия выражаем силу неизвестную  То есть теперь необходимо определить перемещение грузовое и единичное. 6. Начертить грузовое (Г.С.) и единичное состояния (Е.С.) Грузовое состояние – система с внешней нагрузкой  Единичное состояние – система с одной силой, равной одному.  7. Записываем выражения внутренних силовых факторов для грузового состояния и единичного состояния Делим систему на три силовых участка z1, z2 и z3 Участок первый 0 ≤ z1 ≤ a Момент изгибающий грузовой 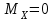 Момент изгибающий единичный 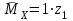 Участок второй 0 ≤ z2 ≤ a Момент изгибающий грузовой 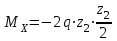 Момент изгибающий единичный  Участок третий 0 ≤ z3 ≤ a Момент изгибающий грузовой  Момент изгибающий единичный 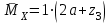 8. Строим эпюру момента изгибающего для единичного состояния Подсчитываем значения внутренних силовых факторов в начале и конце каждого участка. Результаты заносим в таблицу 1. Таблица 1 – Результаты расчета внутренних силовых факторов
По результатам таблицы строим эпюры внутренних усилий 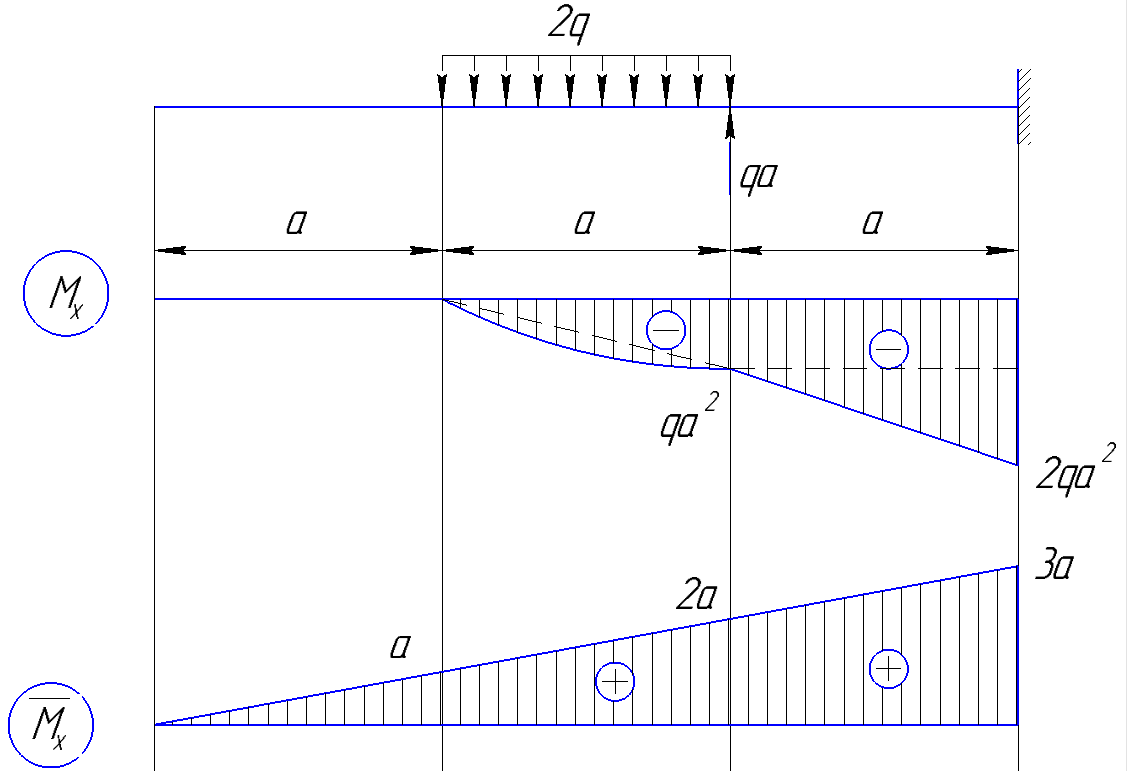 9. Разбиваем эпюру момента изгибающего для грузового состояния на простые фигуры: прямоугольник, треугольник, сегмент. 10. Отмечаем на схеме центр тяжести каждой полученной простой фигуры на эпюре момента изгибающего для грузового состояния 11. Напротив соответствующего центра тяжести каждой полученной простой фигуры показываем на эпюре момента изгибающего для единичного состояния соответствующее значение (ординату) момента изгибающего единичного  12. Методом перемножения площадей эпюры момента изгибающего для грузового состояния на соответствующие ординаты момента единичного (способ Верещагина) определяем грузовое перемещение 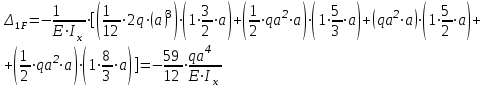 13. Методом перемножения площадей эпюры момента изгибающего для единичного состояния на соответствующие ординаты момента единичного под центрами тяжести простых фигур (способ Верещагина) определяем единичное перемещение  14. По полученным перемещениям используя канонические уравнения находим неизвестную реакцию 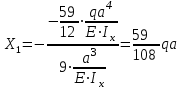 Знак плюс в решении говорит о том, что направление неизвестной силы Х1 было выбрано верно –вверх. 15. Чертим грузовое состояние с найденной неизвестной реакцией 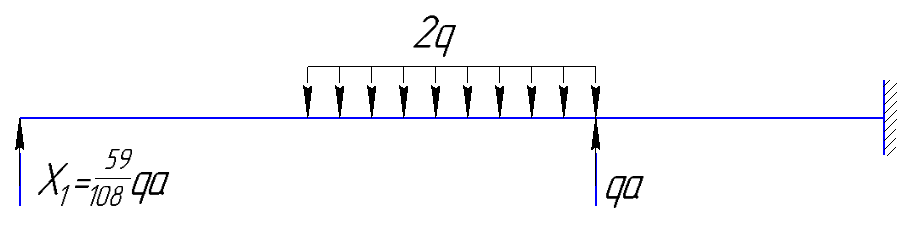 16. Выбираем новую основную систему – оставляем опору, которую убирали в начале, и заменяем жесткую заделку на шарнирно-неподвижную опору. 17. В новой основной системе задаем перемещение: угловое, равное единице в направлении отброшенной связи – момент единичный 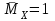 . .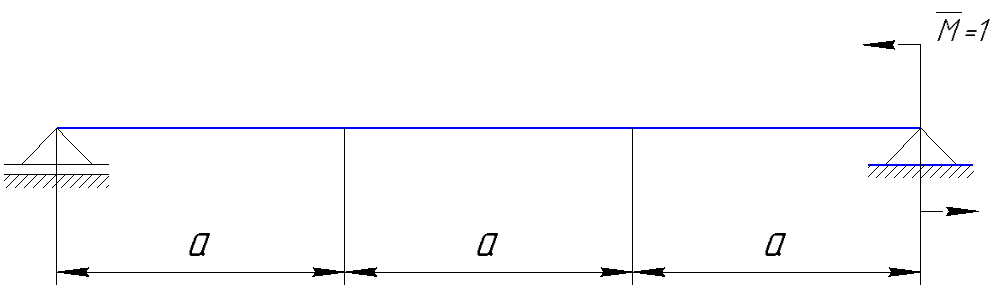 18. Строим эпюры внутренних силовых факторов для грузового состояния с найденной неизвестной реакцией (с раскрытой статической неопределимостью) Делим систему на три силовых участка z1, z2 и z3 Участок первый 0 ≤ z1 ≤ a Сила поперечная 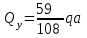 Момент изгибающий грузовой 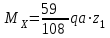 Участок второй 0 ≤ z2 ≤ a Сила поперечная 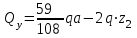 Момент изгибающий грузовой 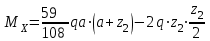 Участок третий 0 ≤ z3 ≤ a Сила поперечная 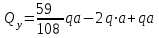 Момент изгибающий грузовой 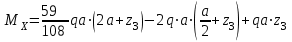 19. Строим эпюры момента изгибающего для новой основной системы Здесь нужно определить реакции в опорах. Находим их из условия равновесия системы – сумма моментов всех сил относительно точки равна нулю. Сумма моментов всех сил относительно точки А: 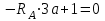 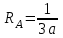 Сумма моментов всех сил относительно точки B: 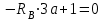 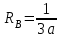 Делим систему на три силовых участка z1, z2 и z3 Участок первый 0 ≤ z1 ≤ a Момент изгибающий единичный 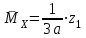 Участок второй 0 ≤ z2 ≤ a Момент изгибающий единичный  Участок третий 0 ≤ z3 ≤ a Момент изгибающий единичный  Подсчитываем значения внутренних силовых факторов в начале и конце каждого участка. Результаты заносим в таблицу 1. Таблица 2 – Результаты расчета внутренних силовых факторов
По результатам таблицы строим эпюры внутренних усилий На втором участке пойдет парабола с вершиной, так как эпюра силы поперечной пересекается с нулевой линией. Приравниваем выражение силы поперечной на втором участке к нулю и находим расстояние пересечения с нулевой линией. 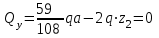 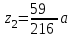 Подставляем данное значение в выражение момента изгибающего для грузового состояния на втором участке 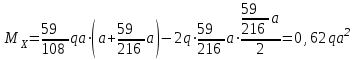 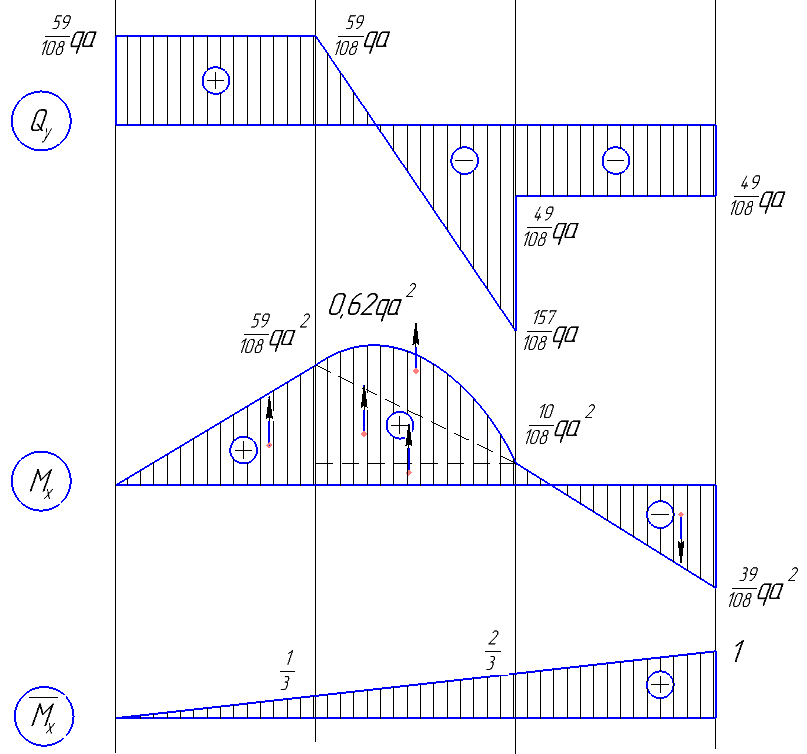 20. Определяем перемещение угловое либо линейное. Разбиваем эпюру момента изгибающего для грузового состояния на простые фигуры: прямоугольник, треугольник, сегмент. Отмечаем на схеме центр тяжести каждой полученной простой фигуры на эпюре момента изгибающего для грузового состояния. Напротив соответствующего центра тяжести каждой полученной простой фигуры показываем на эпюре момента изгибающего для единичного состояния соответствующее значение (ординату) момента изгибающего единичного. Методом перемножения площадей эпюры момента изгибающего для грузового состояния на соответствующие ординаты момента единичного (способ Верещагина) определяем угловое перемещение  Угловое перемещение равно нулю – задача решена верно! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||