курс. Тренировочные задания к экзамену 1 кур 1. Тренировочные задания для подготовки к экзамену по дисциплине Математика 1 курс 1 семестр Часть 1
 Скачать 19.96 Kb. Скачать 19.96 Kb.
|
|
Тренировочные задания для подготовки к экзамену по дисциплине «Математика» 1 курс 1 семестр Часть 1 Развитие понятия о числе. Комплексные числа № 1. Найдите корни уравнения на множестве комплексных чисел: а) х2 + 4х + 12 = 0; б) х2 – 4х + 8 = 0; в) х2 – 6х + 16 = 0; г) 2х2 + х + 1 = 0. № 2. Найдите: z1 + z2; z1 – z2; z1 · z2, если а)z1 = 2 –i и z2 = –1 + 5i; б) )z1 = 3 – 2i и z2 = – 1 –i; в) z1 = – 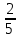 i и z2 = 0,5 – 0,2i. i и z2 = 0,5 – 0,2i. Степени и корни n-й степени № 3. Вычислите: а) (2- 6)- 0,5 • 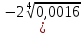 ) + 20; б) ( ) + 20; б) (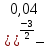 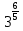 • • 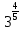 ; ;в) –2 (4-2)-1 • 10-1, г) 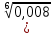 )2 – (– 0,2)-1; д) )2 – (– 0,2)-1; д) 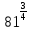 – –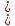 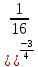 ; ;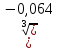 е) 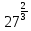 • • 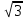 ; ж) 160,25 : 0,0000320,4; з) ; ж) 160,25 : 0,0000320,4; з) 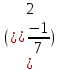 1,4. 1,4.№ 4. Упростите: а) 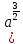 : : 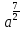 ) • а-4; б) (2х-5)-2 • ) • а-4; б) (2х-5)-2 • 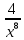 ; в) а8(а-2 – а-4); г) ; в) а8(а-2 – а-4); г) 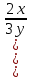 : : 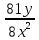 . .№ 5. Найдите значение выражения: а) 2 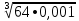 ; б) ; б) 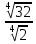 + + 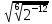 ; ; в) 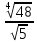 • • 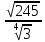 ; г) ; г) 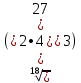 3; д) 3; д) 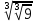 • • 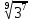 ; ;е) 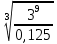 ; ж) ; ж) 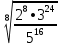 ; ж) ; ж) 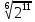 • • 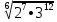 . .№ 6. Упростите выражение: а) 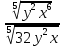 ; б) ; б) 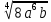 • • 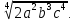 № 7. Представьте число в стандартном виде: а) 25000000; б) 0,00902; в) 10.050.000.000; г) 0,000005. № 8. Сравните числа: а) 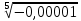 и и 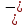 10)-2; б) ( 10)-2; б) ( 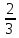 )-2 и 1,52; в) )-2 и 1,52; в) 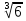 и 1; г) и 1; г) 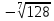 и и 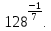 Логарифмы № 9. Найдите: а) 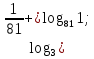 б) б) 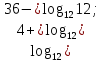 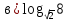 ; ;г) 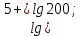 д) д) 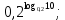 е) е) 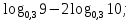 ж) ж) 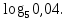 № 10. Сравните: а) 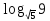 и и 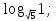 б) б) 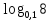 и и 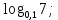 в) в) 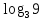 и и 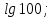 г) г)  10-2. 10-2.Основы тригонометрии № 11. Изобразите на единичной окружности точку, соответствующую углу: а)  = - 405° и определите знаки соs = - 405° и определите знаки соs б)  = - = - 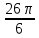 и определите знаки соs и определите знаки соs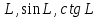 ; ;в) 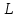 = 1,4π = 1,4π и определите знаки соs и определите знаки соs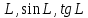 ; ;г) 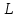 = 2,8π = 2,8π и определите знаки соs и определите знаки соs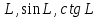 . .№ 12. Найдите знак произведения: а) соs 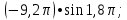 б) 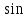 ( (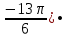 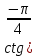 ). ).№ 13. Вычислите: а) 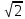 соs соs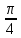 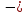 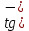 4π); 4π);б) 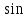 2( 2(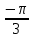 ) + 2 ) + 2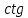 ( (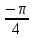 ); );в) соs150° + 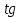 135°; 135°;г) cos (- 540°) - sin 240°. № 14. Упростите, используя формулы тригонометрии: а) 2tg x • ctg x + 1; б) 4 – sin2 x – cos2 x; в) 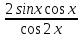 ; ;г) sin x • ctg x – 2 cos x; д) 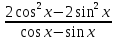 ; ;е) 3cos2 x – 1 + 3 sin2 x; ж) sin40°cos10° - sin10°cos40°. № 15. Найдите sin 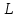 и tg и tg 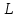 , если сos , если сos 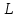 = =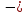 0,6 и 0,6 и 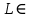 III четверти. III четверти.№ 16. Решите уравнение: а) sin 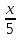 = 1; = 1;б) 4ctg x + 4 = 0; в) 2sin x 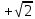 = 0; = 0;г) cos 3x = 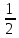 ; ;д) tg x + 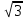 = 0; = 0;е) 2cos 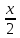 = 0; = 0;ж) sin ( 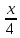 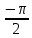 ) + 1 = 0. ) + 1 = 0.Функции, их свойства и графики № 17. Найдите область определения функции: а) у = 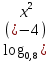 ; б) у = ; б) у = 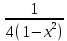 ; в) у = ; в) у = 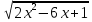 ; ; г) у = 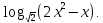 |
