Глава3. Третья трансформаторы тока и схемы их соединения

• Название: Третья трансформаторы тока и схемы их соединения
• Анкор: Глава3.doc
• Дата: 29.01.2017
• Размер: 5.44 Mb.
• Имя файла: Глава3.doc
• Тип: Глава; #993
• страница: 3 из 4

3.5. ТИПОВЫЕ СХЕМЫ СОЕДИНЕНИЯ ОБМОТОК ТРАНСФОРМАТОРОВ ТОКА
Схема соединения ТТ и обмоток реле в полную звезду. Трансформаторы тока устанавливаются во всех фазах. Вторичные обмотки ТТ и обмотки реле соединяются в звезду, и их нулевые точки связываются одним проводом, называемым нулевым (рис. 3.11). В нулевую точку объединяются одноименные зажимы обмоток ТТ. Стрелками показаны условные положительные направления первичных и вторичных токов с учетом полярности обмоток ТТ, начала которых обозначены точками.

При нормальном режиме и трехфазном КЗ, как показано на рис. 3.11, в реле I, II и III проходят токи фаз I_a = I_A/К_I; I_b =I_B/К_I; I_c =I_C/К_I, а в нулевом проводе – их геометрическая сумма:

I_H.П = (I_a + I_b + I_c) (3.12)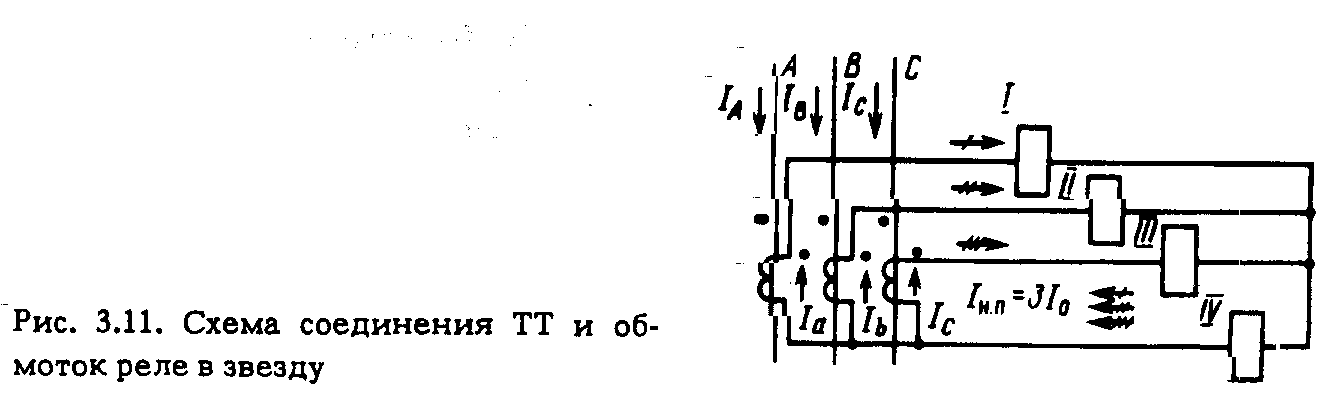



которая при симметричных режимах равна нулю (рис. 3.12, а).

Придвухфазных К 3 ток проходит только в двух поврежденных фазах и соответственно в реле, подключенных к ТТ поврежденных фаз (рис. 3.12, б), ток в неповрежденной фазе отсутствует:

I_C = – I_B.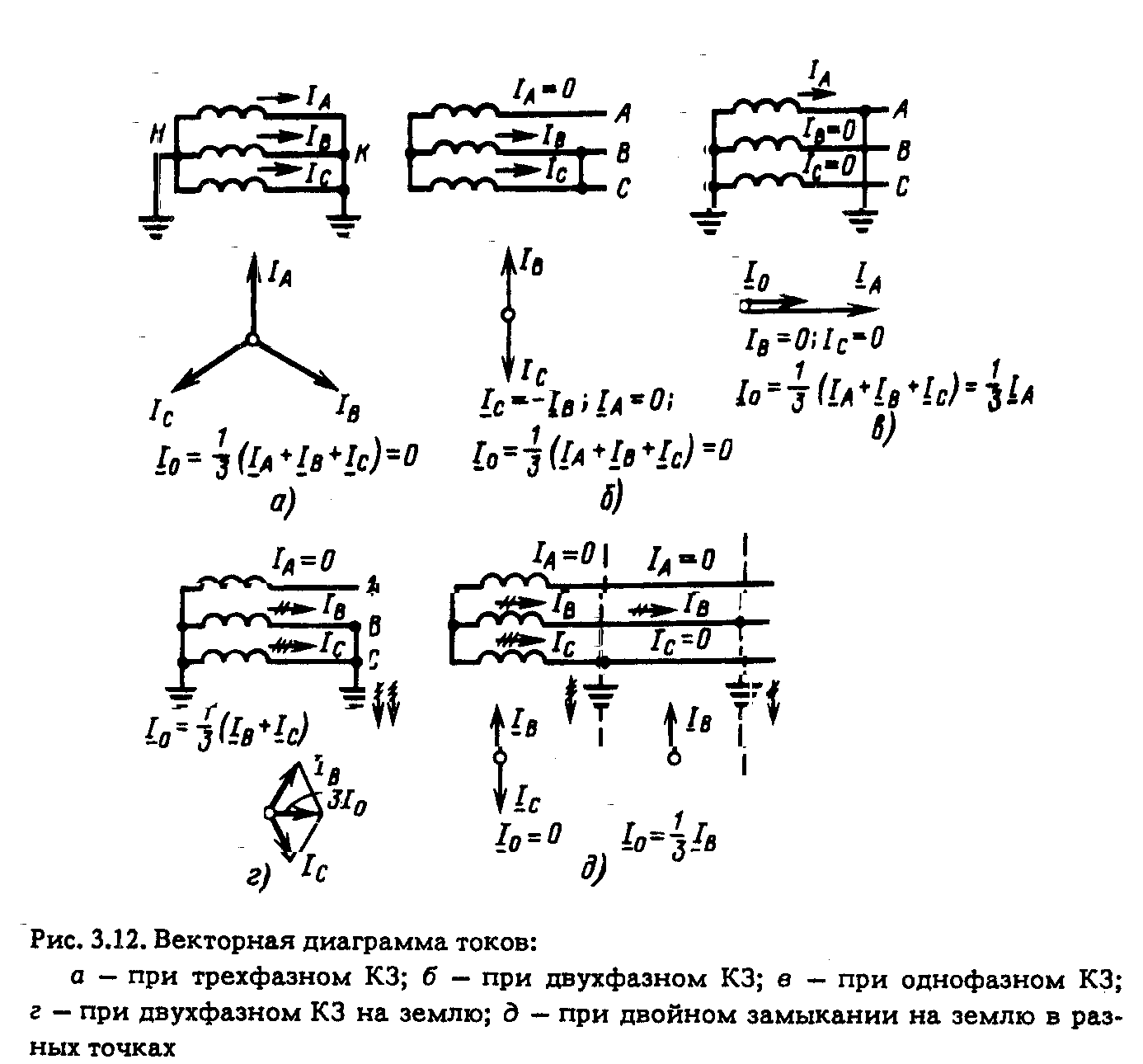



Ток в нулевом проводе отсутствует как в нагрузочном (симметричном) режиме, так и при трех- и двухфазных КЗ. Однако в результате неидентичности характеристик и погрешностей ТТ в нулевом проводе протекает ток небаланса I_H.П = I_HБ: в нормальном режиме он имеет значение 0,01-0,2 А, а при К3 возрастает.

Приоднофазных К3 первичный ток протекает только по одной поврежденной фазе (рис. 3.12, в). Соответствующий ему вторичный ток протекает также только через одно реле и замыкается по нулевому проводу.

При двухфазных КЗ на землю (рис. 3.12,г) ток проходит в двух реле, включенных на поврежденные фазы (например, В и С) (рис. 3.12, г). В нулевом проводе протекает геометрическая сумма этих токов, отличная от нуля.

При двойном замыкании на землю в разных точках протекание токов в сети показано на рис. 3.12, д. На участке между местами замыкания на землю условия аналогичны однофазному КЗ, а между источником питания и ближайшим к нему местом повреждения соответствуют двухфазному КЗ.

Нулевой провод схемы соединения в звезду является фильтром токов НП. Ток I₀ определяется из (3.12). Токи прямой и обратной последовательностей, как видно из рис. 3.13, в нулевом проводе не проходят, так как сумма векторов каждой из этих систем равна нулю (рис. 3.13, б, в). Токи же НП совпадают по фазе и поэтому в нулевом проводе проходит утроенное значение этого тока: I_H.П = 3I₀.

При нарушении (обрыве) вторичной цепи одного из ТТ в нулевом проводе возникает ток, равный току фазы, что может привести к непредусмотренному действию реле, установлен- ному в нулевом проводе. В рассмотренной схеме реле, установленные в фазах, реагируют на все виды КЗ, а реле в нулевом проводе – только на КЗ на землю. Схема соединения ТТ и обмоток реле в звезду применяется в РЗ, действующих при всех видах КЗ.



Как рассматриваемая, так и другие схемы соединения ТТ и реле характеризуются отношением тока в реле I_P к току в фазе I_Ф,которое называется коэффициентом схемы:

k_CX = I_P/I_Ф. (3.13)

Для схемы соединения в звезду k_CX = 1.

Схема соединения ТТ и обмоток реле в неполную звезду. Трансформаторы тока устанавливаются в двух фазах и соединяются так же, как и в схеме соединения в звезду (рис. 3.14, а). В реле I и III проходят токи соответствующих фаз

I_a = I_A/K_I и I_c = I_C/K_I,

а в обратном (общем) проводе (реле IV) ток равен их геометрической сумме:

I_О.П = I_IV = - (I_a + I_c) (3.14)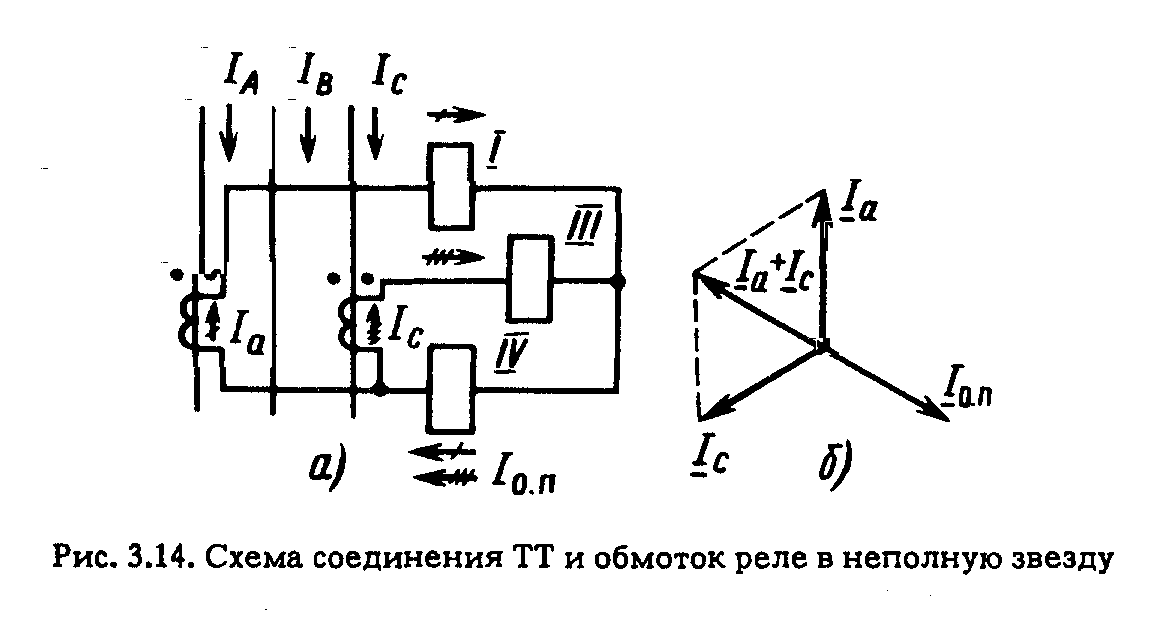



С учетом векторной диаграммы I_a + I_c = – I_b, т. е. I_О.П равен току фазы, отсутствующей во вторичной цепи (рис. 3.14, б).

При трехфазном КЗ и в нормальном режиме токи проходят по обоим реле I и III и в обратном проводе. В случае двухфазного КЗ токи появляются в одном или двух реле (I и III) в зависимости от того, какие фазы повреждены. Ток в обратном проводе при двухфазных КЗ между фазами А и С, в которых установлены ТТ согласно рис. 3.12, б с учетом того, что I_c = – I_a, равен нулю, а при замыканиях между фазами АВ и ВС он соответственно [см. (3.14)] равен: I_О.П = – I_a и : I_О.П = – I_c.

В случае однофазного КЗ фаз (А или С), в которых установлены ТТ, во вторичной обмотке ТТ и обратном проводе проходит ток КЗ. При замыкании на землю фазы В, в которой ТТ не установлен, токи в РЗ не появляются. Коэффициент схемы k_CX = 1.

Схема соединения ТТ в треугольник, а обмоток реле в звезду. Вторичные обмотки ТТ, соединенные последовательно разно- именными выводами (рис. 3.15), образуют треугольник. Реле, соединенные в звезду, подключаются к вершинам треугольника. Из токораспределения видно, что в каждом реле протекает ток, равный геометрической разности токов двух фаз:

I_I = I_A/K_I – I_B/K_I,

I_II = I_B/K_I – I_C/K_I,

I_III = I_C/K_I – I_A/K_I,
При симметричной нагрузке и трехфазном КЗ в реле проходит ток, в 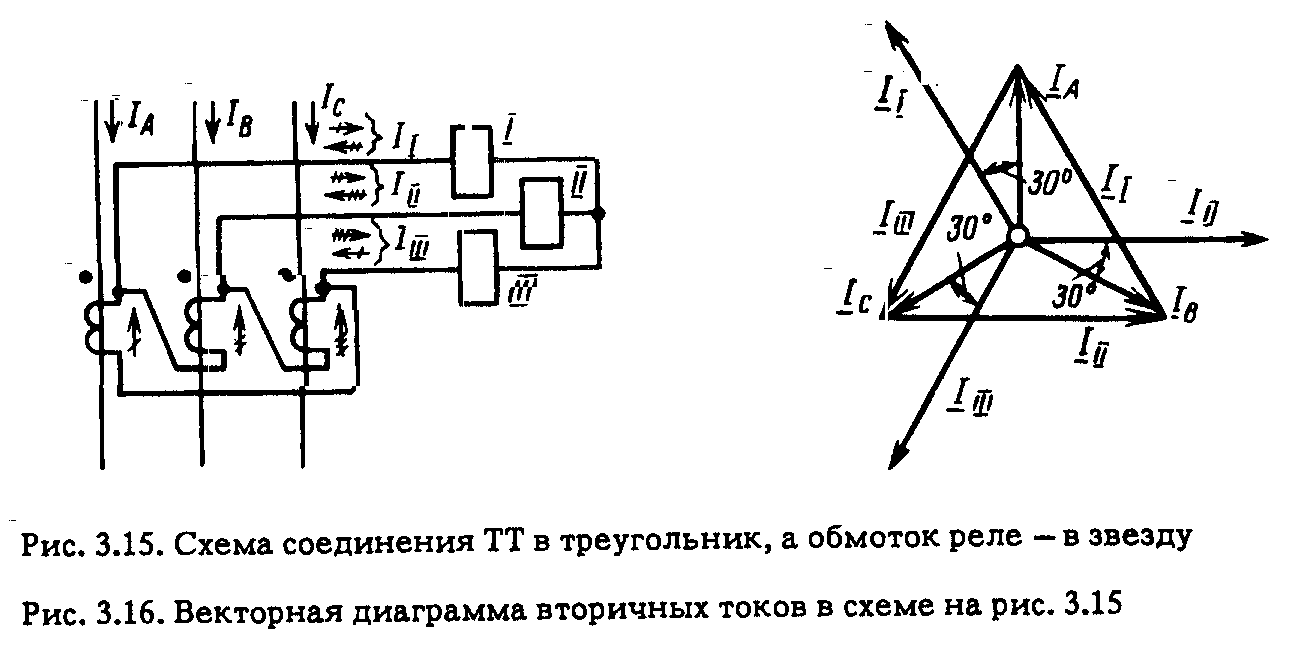раз больший тока фазы и сдвинутый относительно него по фазе на 30^o (рис. 3.16).


В табл. 3.2 приведены значения токов при других видах КЗ в предположении, что коэффициент трансформации ТТ равен единице. Схема соединений ТТ в треугольник обладает следующими особенностями:

токи в реле протекают при всех видах КЗ;

РЗ по такой схеме реагируют на все виды повреждений;

отношение тока в реле к фазному току зависит от вида КЗ; токи НП не выходят за пределы треугольника.



Отсюда следует, что при КЗ на землю в реле попадают только прямая и обратная последовательности, т.е. только часть тока КЗ. Описанная выше схема применяется в основном для дифференциальных и дистанционных РЗ.

Поскольку в рассматриваемой схеме ток в реле при трехфазных симметричных режимах в 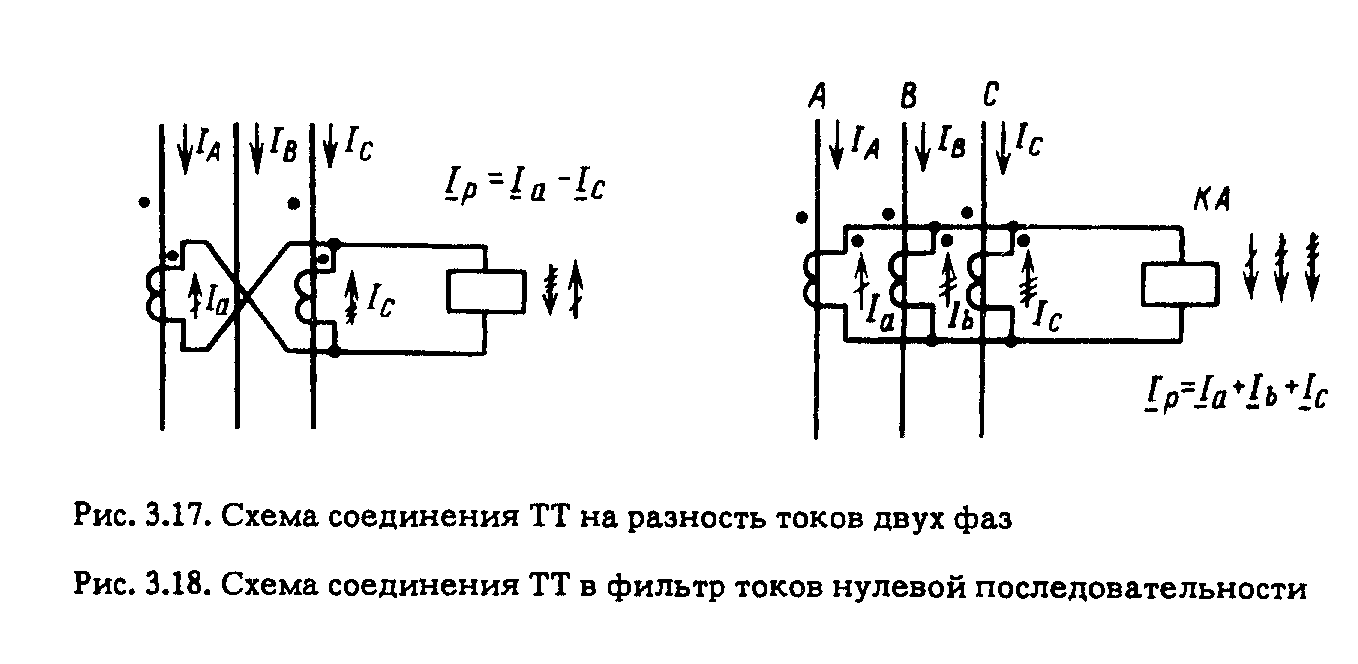раз больше тока в фазе, коэффициент схемы согласно (3.13) равен:





Схема соединения с двумя ТТ и одним реле, включенным на разность токов двух фаз. Трансформаторы тока устанавливаются в двух фазах (например, А и С на рис. 3.17); их вторичные обмотки соединяются разноименными зажимами, к которым подключается обмотка реле. Из токораспределения, показанного на рис. 3.17 для случая, когда по первичной цепи проходят положительные токи I_A, I_B, I_C, находим, что ток в реле I_P равен геометрической разности токов двух фаз I_a и I_c, т. е.

I_P = I_a – I_c, (3.15)

где I_a = I_A /К_I; I_c = I_C /К_I.

При симметричной нагрузке и трехфазном КЗ разность токов I_a – I_c враз больше тока в фазе (I_a и I_c) и, следовательно,

(3. 15а)

При двухфазном КЗ АС (фазы, на которых установлены ТТ):

(3.156)

где I_Ф = |I_a| = |I_c|.

При двухфазных КЗ АВ или ВС в реле поступает ток только одной фазы I_a или I_c:

(3. 15в)

где I_Ф = I_a или I_Ф = I_с.

Из (3.15а) – (3.15в) следует, что данная схема по сравнению со схемами полной и двухфазной звезды имеет худшую в раз чувствительность при КЗ между фазами АВ и ВС.

В случае двухфазного КЗ между фазами В и С за силовым трансформатором с соединением обмоток звезда – треугольник ток в реле I_P = I_a – I_c, оказывается равным нулю, так как токи I_a и I_c, равны по значению и совпадают по фазе, что видно из токораспределения на рис. 3.19.

Рассматриваемая схема может применяться только для РЗ от междуфазных КЗ в тех случаях, когда она обеспечивает необходимую чувствительность при двухфазных КЗ и когда не требуется ее действие при КЗ за трансформатором с соединением обмотки . Коэффициент схемы при симметричных режимах

Схема соединения ТТ в фильтр токов НП. Трансформаторы тока устанавливаются на трех фазах, одноименные зажимы вторичных обмоток соединяются параллельно, и к ним подключается обмотка реле КА (рис. 3.18). Ток в реле равен геометрической сумме вторичных токов трех фаз:

I_P = I_a + I_b + I_c = 3I₀.

Рассматриваемая схема является фильтром токов НП. Ток в реле появляется только при одно- и двухфазных КЗ на землю. Поэтому схема применяется для РЗ от КЗ на землю.

Включение реле по схеме на рис. 3.18 равносильно его включению в нулевой провод звезды по рис. 3.11.

Анализ работы схем соединения ТТ при двухфазных КЗ за трансформаторами с соединением обмоток 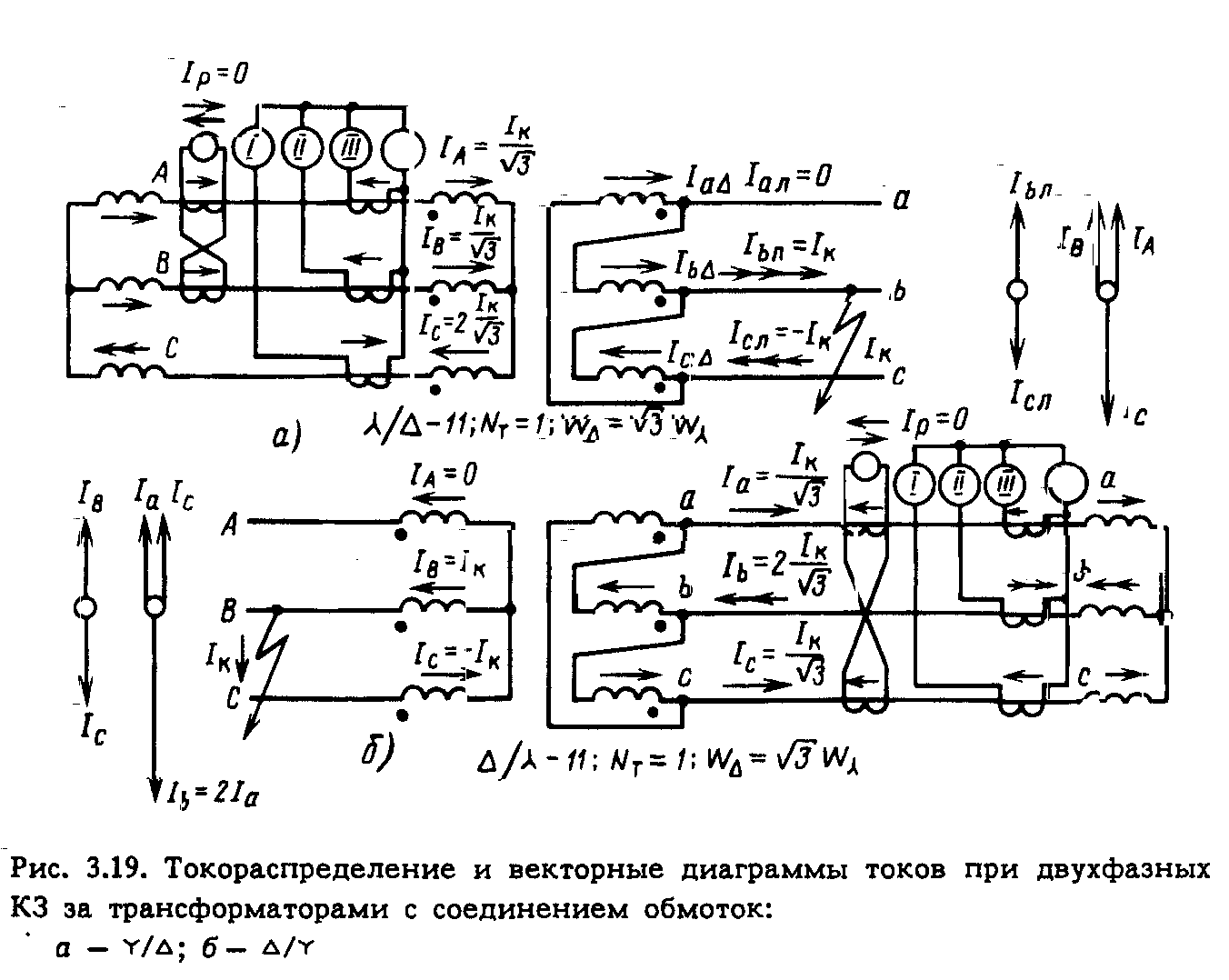или . Особым случаем по характеру токораспределения являются двухфазные КЗ за трансформаторами с соединением обмоток или .



Токораспределение на стороне звезды трансформатора с соединением обмоток (рис. 3.19, а) при КЗ на стороне треугольника. Для простоты принимается, что коэффициент трансформации трансформатора N_T = 1. При этом отношение линейных токов обмоток с соединением равно 1, а токов в фазах

(3.16)

При двухфазном КЗ на стороне треугольника, например между фазами b и с (рис. 3.19, а), ток в неповрежденной фазе I_a = 0, а токи в поврежденных фазах b и с равны току КЗ, т. е.

I_c = – I_b = I_k.

Как видно из рис. 3.19, а, в треугольнике ток I_K делится на две части: одна замыкается по обмотке фазы с и другая – по последовательно включенным обмоткам фаз b и с. Поскольку сопротивление второй цепи в 2 раза больше, чем первой, ток в обмотке фазы с равен , а в обмотках а и b .

Токи на стороне звезды соответствуют токам в обмотках одноименных фаз треугольника и превышают их с учетом (3.16) в раз:





(3.17)

При К3 между фазами аb и са картина распределения токов будет аналогичной. Таким образом, при двухфазном КЗ на стороне треугольника трансформатора токи на стороне звезды появляются во всех трех фазах. В двух фазах они равны и одинаково направлены. В третьей фазе ток противоположен первым двум и равен их сумме, т.е. в 2 раза больше каждого из них.

Токораспределение на стороне треугольника при двухфазном КЗ за трансформатором с соединением обмоток (рис. 3.19, б). Распределение и соотношение токов на стороне треугольника получается аналогично предыдущему случаю на стороне звезды. Анализ условий работы максимальных токовых РЗ (МТЗ), подключенных к ТТ, соединенным по разным схемам, при КЗ за трансформатором (или ) показывает:

1) в схеме полной звезды (рис. 3.19, б) в одной фазе схемы

появляется ток , а в двух других ; сумма токов в нулевом проводе равна нулю. Реле I, II, III действуют, но два из них имеют в 2 раза меньшую чувствительность, чем третье;

2) в схеме неполной звезды ток проходит по обеим фазам и обратному проводу, в последнем он равен геометрической сумме токов указанных фаз или току фазы, отсутствующей в схеме.

Если ТТ окажутся на фазах с меньшими первичными токами , то в таком случае условие чувствительности будет в 2 раза хуже, чем в схеме полной звезды. Для устранения этого недостатка следует использовать реле в обратном проводе, где проходит сумма токов фаз, равная току КЗ в третьей фазе:



3) в схеме с включением одного реле на разность токов двух фаз ток в реле в случае, показанном на рис. 3.19, а, б, будет отсутствовать.

3.6. НАГРУЗКА ТРАНСФОРМАТОРОВ ТОКА

Погрешность ТТ зависит от его нагрузки, сопротивление которой

Z_H = U₂/I₂, (3.18)

где U₂ и I₂ – напряжение и ток вторичной обмотки (рис. 3.20, а).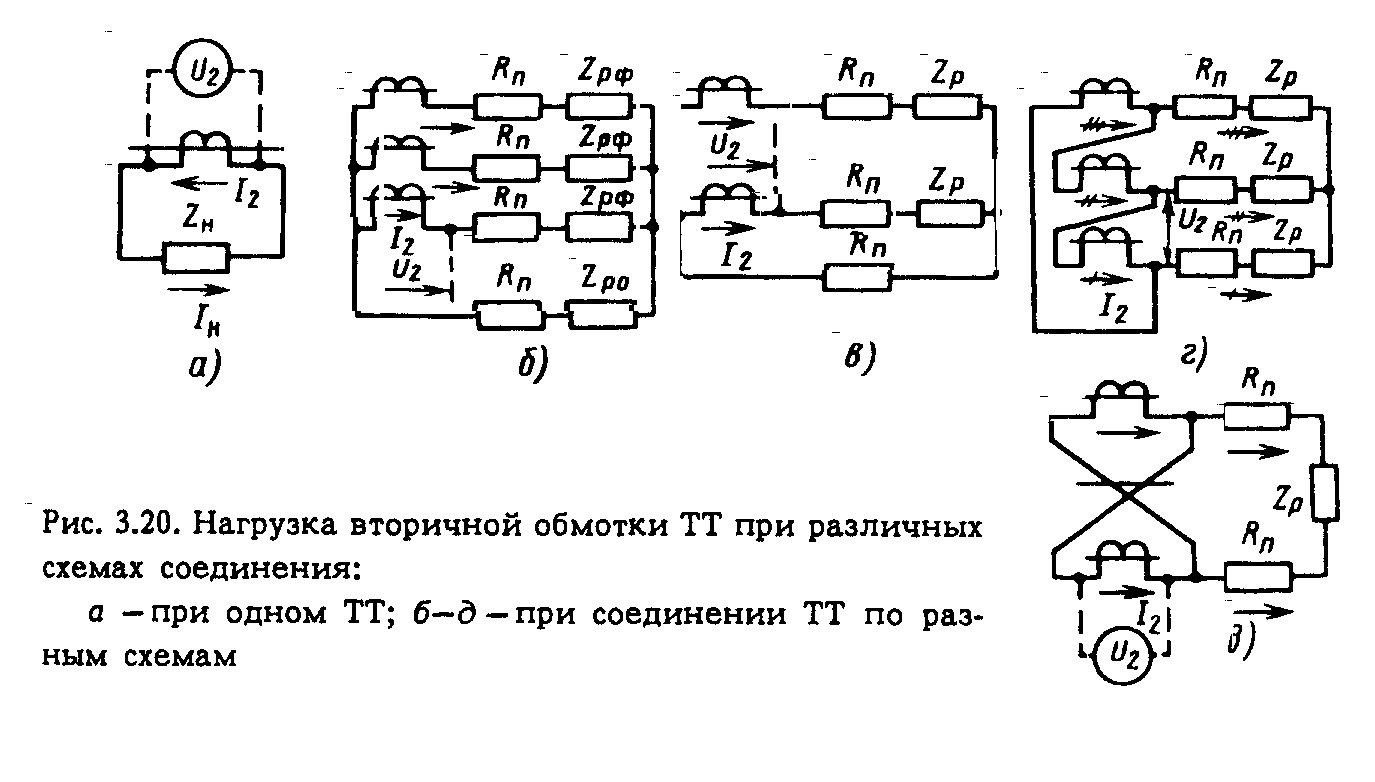



Сопротивление нагрузки состоит из сопротивлений проводов R_П и реле Z_P, которые для упрощения суммируются арифметически: Z_H = R_П + Z_P. Значение U₂ = I₂Z_H (рис. 3.20, а) зависит от схемы соединений ТТ, сопротивления нагрузки Z_H , вида КЗ и сочетания поврежденных фаз.

Для схемы полной звезды (рис. 3.20, б) напряжение U₂ при трех- и двухфазных КЗ равно падению напряжения в нагрузке фазы:

U₂ = I₂(R_П + Z_Р.Ф),

поэтому



172

При однофазном К3 U₂ равно падению напряжения в сопротивлении петли "фаза-нуль" (2R_П) и в сопротивлении реле в фазе Z_Р.Ф и нулевом проводе Z_Р.O:



Таким образом, наибольшее Z_H получается при однофазном К3.

В схеме неполной звезды (рис. 3.20, в) максимальная нагрузка на ТТ имеет место при двухфазных КЗ между фазой, имеющей ТТ, и фазой, не имеющей его:

Z_H = 2R_П + Z_P.O.

В схеме включения реле на разность токов двух фаз (рис. 3.20, д) наибольшая нагрузка получается при двухфазных КЗ между фазами, имеющими ТТ:

I_P = 2I₂;

В схеме треугольника (рис. 3.20,г) ТТ имеют наибольшую нагрузку как при трехфазном, так и при двухфазном КЗ. В обоих случаях

Z_H = 3R_П + Z_P.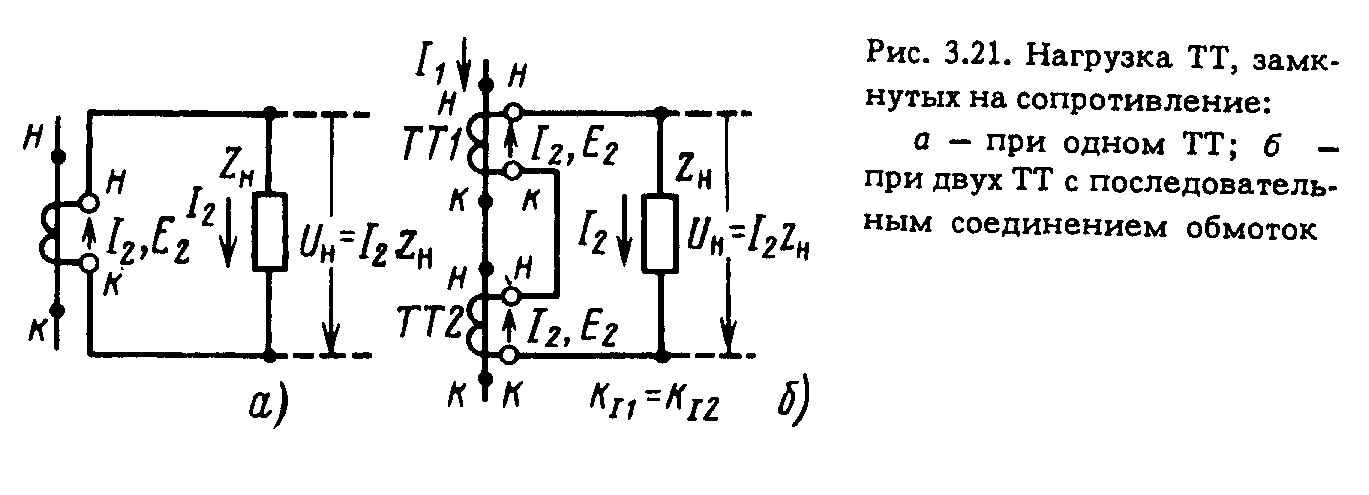



Для уменьшения нагрузки ТТ при их недостаточной мощности можно применять последовательное включение двух ТТ, установленных на одной фазе (рис. 3.21) с одинаковым коэффициентом K_I. В этом случае падение напряжения в нагрузке делится поровну между вторичными обмотками ТТ.