Зачет по геометрии. Зачет 9а класс.. Треугольники

• Название: Треугольники
• Анкор: Зачет по геометрии
• Дата: 24.03.2022
• Размер: 145.5 Kb.
• Имя файла: Зачет 9а класс..doc
• Тип: Решение; #414136

ТРЕУГОЛЬНИКИ

13. В пря­мо­уголь­ном треугольнике один из ка­те­тов равен 10, а угол, ле­жа­щий напротив него, равен 45°. Най­ди­те площадь треугольника.

Решение.

Так как в пря­мо­уголь­ном треугольнике один из углов равен 45°, то такой тре­уголь­ник является равнобедренным. Пло­щадь прямоугольного тре­уголь­ни­ка равна по­ло­ви­не произведения катетов. Таким образом:

 



 

 

Ответ: 50.

Ответ: 50

169840

50

14. Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 28 и 100.

15. Решение.

Пусть ка­те­ты имеют длины и а ги­по­те­ну­за — длину Пусть длина высоты, проведённой к ги­по­те­ну­зе равна Найдём длину не­из­вест­но­го ка­те­та из тео­ре­мы Пифагора:

 



 

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка может быть най­де­на как по­ло­ви­на про­из­ве­де­ния ка­те­тов:

 



Ответ: 1344.

Ответ: 1344

323159

1344

1 В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 4, а ост­рый угол, при­ле­жа­щий к нему, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Решение.

Сумма углов в тре­уголь­ни­ке равна 180°, по­это­му вто­рой ост­рый угол равен 180° − 90° − 45° = 45°. Оба ост­рых угла равны, следовательно, дан­ный тре­уголь­ник — равнобедренный, от­ку­да получаем, что вто­рой катет равен 4. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния катетов:

 

Ответ: 8.

Ответ: 8

323282

8

16.В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

Решение.

Сумма углов в тре­уголь­ни­ке равна 180°, по­это­му вто­рой ост­рый угол равен 180° − 90° − 45° = 45°. Оба ост­рых угла равны, следовательно, дан­ный тре­уголь­ник — равнобедренный, от­ку­да получаем, что оба ка­те­та равны. Длина ка­те­та равна Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния катетов:

 

Ответ: 1225.

Ответ: 1225

323356

1225

17. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

24. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Решение.

Пусть — длина ос­но­ва­ния рав­но­бед­рен­но­го треугольника, — длина бо­ко­вой сто­ро­ны рав­но­бед­рен­но­го треугольника, — высота, проведенная к основанию . Вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка, проедённая к основанию, также яв­ля­ет­ся его бис­сек­три­сой и медианой. Из пря­мо­уголь­но­го тре­уголь­ни­ка найдём вы­со­ту по тео­ре­ме Пифагора:

 



 

Площадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния ос­но­ва­ния на высоту:

 



Ответ: 480.

Ответ: 480

323179

480

25. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка

ТРАПЕЦИЯ

26. 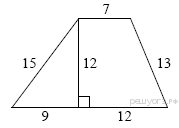Най­ди­те площадь трапеции, изображённой на рисунке.

Решение.

Площадь тра­пе­ции равна про­из­ве­де­нию полусуммы ос­но­ва­ний на высоту:

 



 

 

Ответ: 168.

Ответ: 168

39

168

Источник: Демонстрационная вер­сия ГИА—2013 по математике.

27.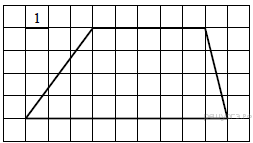

Найдите пло­щадь трапеции, изображённой на рисунке.

Решение.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту:

 



 

 

Ответ: 28.

Ответ: 28

117

28

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.

28.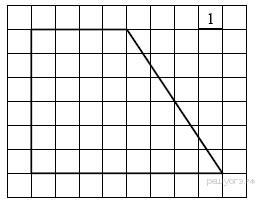

Найдите пло­щадь трапеции, изображённой на рисунке.

Решение.

Пло­щадь тра­пе­ции равна про­из­ве­де­нию по­лу­сум­мы ос­но­ва­ний на вы­со­ту:

 



 

 

Ответ: 36.

Ответ: 36

143

36

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.

Решение.

Площадь трапеции равна произведению полусуммы оснований на высоту:

 



 

Ответ: 36.

Ответ: 36

169

36

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317.

29. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна , а угол ме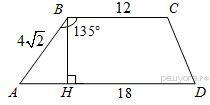жду ней и одним из ос­но­ва­ний равен 135°. Най­ди­те площадь трапеции.

Решение.



Пусть дана тра­пе­ция ABCD, где AD = 18, BC = 12, AB = , а ∠ABC = 135°. Опу­стим перпендикуляр BH на сторонуAD. Угол ABH равен: 135° − 90° = 45°. Таким об­ра­зом, треугольник ABH яв­ля­ет­ся прямоугольным и равнобедренным. Най­дем высоту BH:

 



 

Площадь тра­пе­ции равна произведению по­лу­сум­му оснований на высоту:

 



 

Ответ: 60.

Ответ: 60

169881

60

30. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен . Най­ди­те площадь трапеции.

Треугольники общего вида

1. В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее высота — 5. Най­ди­те площадь треугольника.

Решение.

Площадь тре­уголь­ни­ка равна по­ло­ви­не произведения вы­со­ты на основание. Таким образом:

 



Ответ: 25.

Ответ: 25

169853

25

2. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 60°. Най­ди­те площадь треугольника.

Решение.

Площадь тре­уголь­ни­ка равна по­ло­ви­не произведения сто­рон на синус угла между ними. Имеем:

 



Ответ: 75.

Ответ: 75

169854

75

3.

Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

Параллелограмм

1.

Найдите пло­щадь параллелограмма, изображённого на рисунке.

Решение.

Площадь па­рал­ле­ло­грам­ма равна про­из­ве­де­нию длины ос­но­ва­ния на высоту:

 



 

 

Ответ: 40.

Ответ: 40

65

40

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1301.

2. Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

Решение.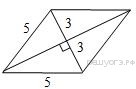



Диагонали ромба пе­ре­се­ка­ют­ся под углом 90° и точ­кой пересечения де­лят­ся пополам. Из пря­мо­уголь­но­го треугольника, ка­те­та­ми которого яв­ля­ют­ся половины диа­го­на­лей ромба, а ги­по­те­ну­зой — сто­ро­на ромба, по тео­ре­ме Пифагора най­дем половину не­из­вест­ной диагонали: Тогда вся не­из­вест­ная диагональ равна 8.

Площадь ромба равна по­ло­ви­не произведения диагоналей:

 



Ответ: 24.

Ответ: 24

169868

24

3. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Решение.

Периметр ромба равен сумме длин всех его сторон. Так как все сто­ро­ны равны, сто­ро­на ромба равна 10. Пло­щадь ромба равна про­из­ве­де­нию сто­рон на синус угла между ними. Таким образом,

 



Ответ: 50.

Ответ: 50

169869

50

4. Периметр ромба равен 24, а синус од­но­го из углов равен . Най­ди­те площадь ромба.

Решение.

Периметр ромба равен сумме длин всех его сторон. Так как все сто­ро­ны равны, сто­ро­на ромба равна 6. Пло­щадь ромба равна про­из­ве­де­нию сторон на синус угла между ними, поэтому

 



 

Ответ: 12.

Ответ: 12

169872

12

5. Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

12.

Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

Решение.

Площадь ромба можно найти как по­ло­ви­ну произведения его диагоналей:

 

Ответ: 42.

Ответ: 42

323957

42

13.

Сто­ро­на 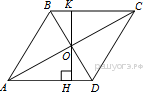ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

Решение.

Проведём по­стро­е­ние и введём обо­зна­че­ния как по­ка­за­но на рисунке. Учитывая, что и по­лу­ча­ем Диа­го­на­ли ромба точ­кой пе­ре­се­че­ния де­лят­ся пополам. Рас­смот­рим тре­уголь­ни­ки и , они прямоугольные, следовательно, тре­уголь­ни­ки и равны, от­ку­да то есть вы­со­та Найдём пло­щадь ромба как про­из­ве­де­ние сто­ро­ны на высоту:

 



 

Ответ: 18.

Ответ: 18

324017

18

14. Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

Решение.



Введём обо­зна­че­ния как по­ка­за­но на рисунке. Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и де­лят­ся точ­кой пе­ре­се­че­ния пополам. Пусть Рас­смот­рим тре­уголь­ник он прямоугольный, из тео­ре­мы Пи­фа­го­ра найдём

 



 

Найдём пло­щадь ромба как по­ло­ви­ну про­из­ве­де­ния его диагоналей:

 



 

Ответ: 2400.

Ответ: 2400

324097

2400

15. Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

Решение.

Проведём вы­со­ту в ромбе и введём обо­зна­че­ния как по­ка­за­но на рисунке. Все сто­ро­ны ромба равны, по­это­му Найдём из пря­мо­уголь­но­го треугольника

 



 

Найдём пло­щадь ромба как про­из­ве­де­ние стороны на высоту:

 



 

Ответ: 420,5.

Ответ: 420,5

324117

420,5

16.

Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.