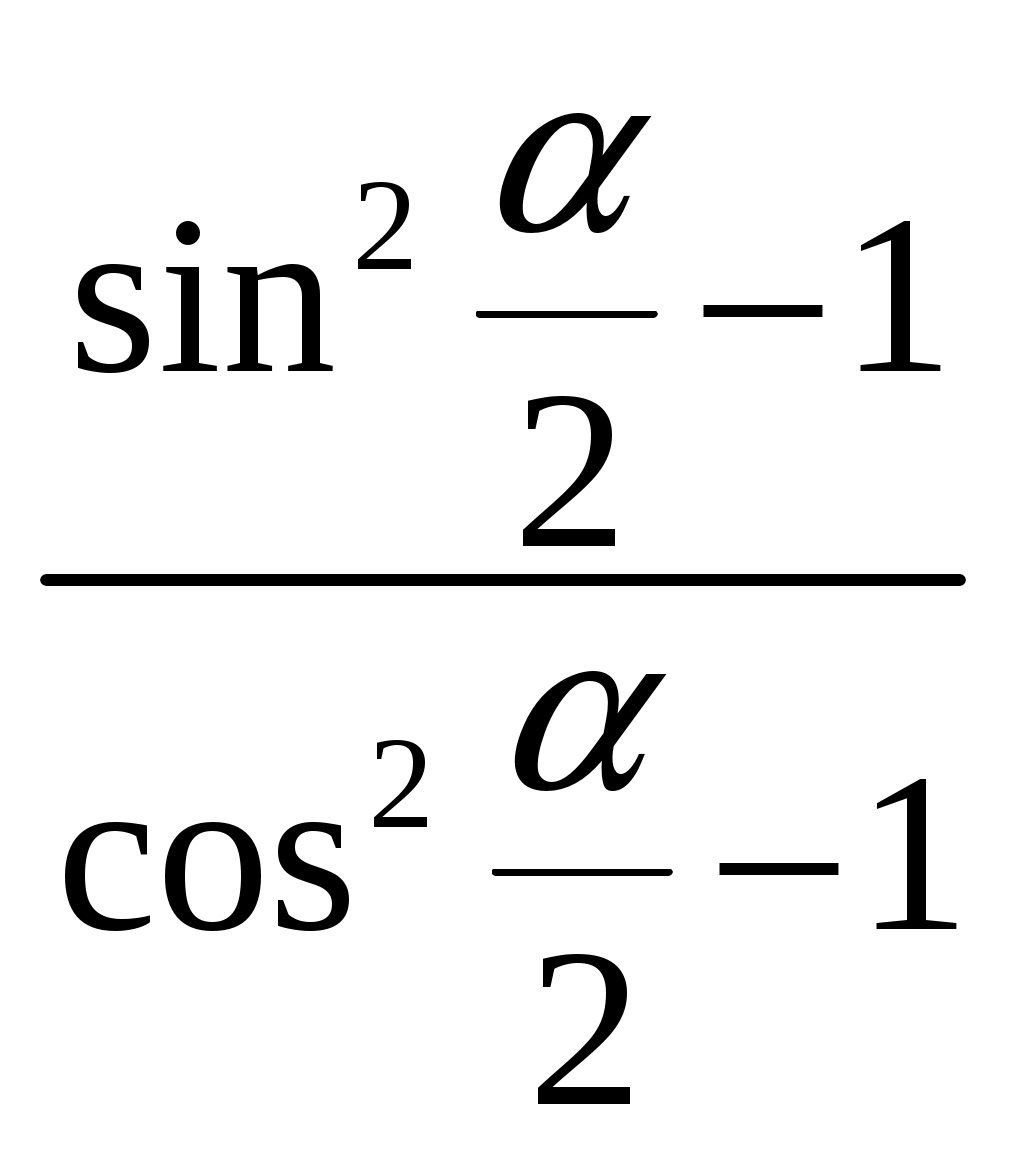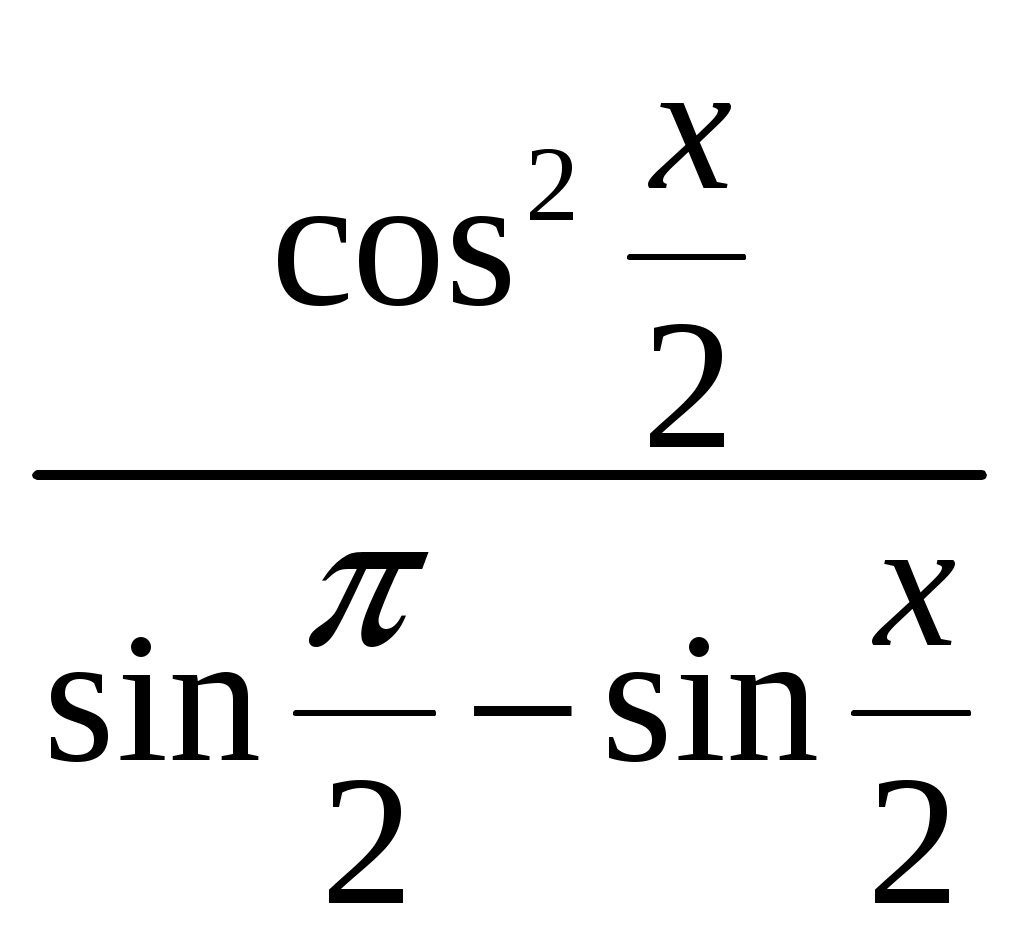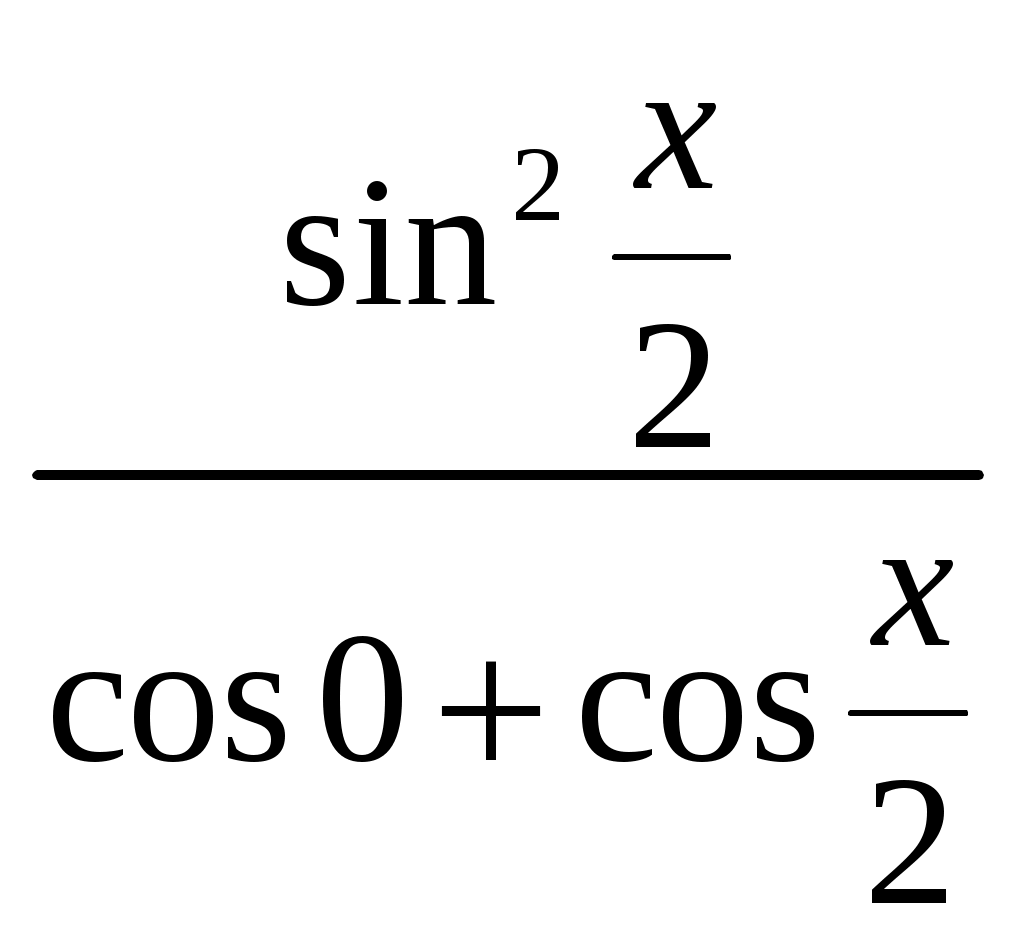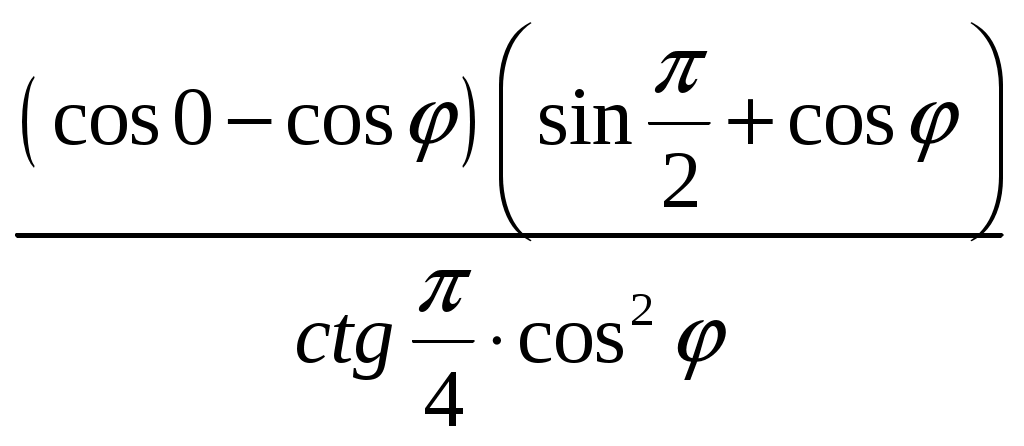Тригонометрические функции Урок Числовая окружность Цели урока
 Скачать 323 Kb.
|
Глава 1. Тригонометрические функцииУрок 7. Числовая окружностьЦели урока: ввести понятие числовой окружности; сформулировать умения записывать множество чисел, соответствующих на числовой окружности точке; закрепить умение находить на числовой окружности точку, соответствующую данному числу. Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Проверка домашнего задания. Опрос по теории: 1. Какая окружность называется числовой? 2. Где на числовой окружности находятся числа  ?3. Как записать множество чисел, соответствующих на числовой окружности точке? 4. Опишите первый макет числовой окружности. 5. Опишите второй макет числовой окружности. III. Закрепление нового материала. Выходят к доске сразу 4 учащихся и решают №1 одновременно, а остальные учащиеся, решая в тетрадях, проверяют работу у доски. Необходимо создать атмосферу творческого поиска, если будет спор, то умело его поддерживать, и находить верное решение совместно. Затем по той же схеме решается №3. На доске изображаются 4 числовые окружности, на которых учащиеся будут показывать точки, которые соответствуют числам из №9-16. Учитель вызывает учащихся к доске без определенного порядка. IV. Решение заданий у доски. Решение заданий из №20, 24, 25 проходит так: учитель решает с полным объяснением у доски в каждом номере букву (а), а остальные буквы в заданиях решают у доски учащиеся. Подведение итогов. Домашнее задание: №2, 4; теория в учебнике, стр. 8-18; разобрать пример 7 из теории. Урок 8. Числовая окружность на координатной плоскостиЦели урока: рассмотреть числовую окружность на координатной плоскости; составить таблицу значений; закрепить умение нахождение на числовой окружности точки с конкретным значением абсциссы и ординаты, а также умением определить каким числам они соответствуют. Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Проверка домашнего задания. Проверить домашнюю работу можно проверочной работой в четырех вариантах:
III. Объяснение нового материала. Объяснение нового материала (стр. 18-26): 1. Рассмотреть числовую окружность в декартовой системе координат. 2. Составить таблицу координат чисел числовой окружности для первого макета. 3. Составить таблицу координат чисел числовой окружности для второго макета. IV. Закрепление нового материала. На доске изображаются 4 числовые окружности на координатной плоскости, на которых выполняются задания из №29-34(а, б, в). Подведение итогов. Домашнее задание: №29-34 (г); теория в учебнике, стр. 18-26; разобрать пример из теории. Урок 9. Синус и косинусЦели урока: ввести понятие синуса и косинуса; рассмотреть их свойства; составить таблицу их значений. Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Проверочная работа. На доске изображаются первый и второй макет числовой окружности на координатной плоскости (смотри рисунок 1 и 2). Работа поводится в четырех вариантах. Все задания приведены в таблице.
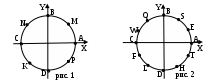 III. Объяснение нового материала. Объяснение нового материала (стр. 26-28): 1. Ввести понятия синуса и косинуса, как координаты точки единичной окружности. 2. Вывести основное тождество тригонометрии. IV. Закрепление нового материала. Решение заданий из №50-54 (а, г), №55 (а, б), №60, 62. на единичной окружности. Подведение итогов. Домашнее задание: №57, 61; теория в учебнике, стр. 26-28; разобрать пример из теории. Урок 10. Синус и косинусЦели урока: закрепить понятие синуса и косинуса; рассмотреть решение уравнений вида  и  ; вывести формулы  и  Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Математический диктант. Вычислить  и  , если t может принимать значения ,  ,  ,  ,  ,  ,  ,  .III. Объяснение нового материала. Объяснение нового материала (стр. 28-34): 1. Рассмотреть решение уравнения на окружности, где  принимает одно из значений  (примеры 2 и 6).2. Рассмотреть решение уравнения на окружности, где принимает одно из значений  (примеры 3 и7)3. Доказать справедливость равенств и .IV. Решение заданий у доски. После рассмотрения примера 2 решают №63 (б, г), №64 (а), после примера 6 решают №67 (а, в), после примера 3 решают №63 (а, в), №64 (б, в, г), после примера 7 решают №67 (б, г). Подведение итогов. Домашнее задание: №55 (в, г), №65, 66, 68; теория в учебнике, стр. 30-34. Урок 11. Тангенс и котангенсЦели урока: ввести определение тангенса и котангенса; рассмотреть их свойства; составить таблицу их значений; закрепить понятие синуса, косинуса, тангенса и котангенса; закрепить умение использовать свойства тригонометрических функций. Ход урока I . Организационный момент. Приветствие, сообщение темы и задач урока. II. Работа с учебником. Учащиеся читают теоретический материал на стр. 34-37. Учитель по мере прочтения задает вопросы учащимся: 1. Почему тангенсом считается отношение синуса к косинусу? 2. При каких условиях существует тангенс? Почему? 3. При каких условиях существует котангенс? Почему? 4. Как вычисляется тангенс числа? 5. Вычислите  ,  ,  ,  .6. Объясните формулы  и  .7. Вычислите  ,  ,  ,  .Затем вызываются к доске два учащихся для обобщения прочитанного. III. Решение заданий у доски. Решение заданий из №94 – 96 у доски учащимися из группы А. Решение заданий из №97, 100 у доски учащимися из группы Б. Подведение итогов. Домашнее задание: №98, 99; теория в учебнике, стр. 34-37. Урок 12. Тригонометрические функции числового аргументаЦели урока: ввести понятие тригонометрической функции числового аргумента; вывести основные формулы одного аргумента тригонометрических функций; формировать умение упрощать выражения с применением основных формул одного аргумента тригонометрических. Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Объяснение нового материала. Объяснение нового материала (стр. 37-39): 1. Вспомните соотношения, связывающие различные тригонометрические функции одного и того же угла. 2. Решить задачу: «Найти соответствующее значение ,  ,  , если известно, что  и  .»III. Закрепление нового материала. Решение заданий из №110, 111 устно с места, уточняя какую формулу применяли. К доске работать выходят по одному 4 учащихся, объясняя подробно, решать задания из №112 (а), №116 (а); №112 (б), №117 (а); №112 (в), №118 (а); №112 (г), №119 (а). IV. Решение заданий у доски. К доске выходят сразу 4 учащихся решать три задания:
V. Проверочная работа. Остальные учащиеся решают на месте по вариантам:
Подведение итогов. Домашнее задание: №115, №116-119 (г); теория в учебнике, стр. 37-39. Урок 13. Тригонометрические функции числового аргументаЦели урока: закреплять умение упрощать выражения с применением основных формул одного аргумента тригонометрических функций; развить навыки упрощение выражений с применением основных формул одного аргумента тригонометрических функций. Ход урока I. Организационный момент. Приветствие, сообщение темы и задач урока. II. Проверочная работа. Проверить знание теоретического материала можно проверочной работой в четырех вариантах:
III. Проверка домашнего задания. Пока 4 учащихся решают у доски №115 остальные устно комментируют промежуточные действия в заданиях №116-119 (г). IV. Самостоятельная работа.
Подведение итогов. Домашнее задание: №120; теория в учебнике, стр. 40-43. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
.
.
.
.
.
.
.
, 
. Вычислите 
.
, 
.
, 
. Вычислите 
.
, 
. Вычислите 
.
