тригонометричні рівняння. Тригонометричні рівняння. Їх види та способи розвязування
 Скачать 59.88 Kb. Скачать 59.88 Kb.
|
     Міністерство освіти і науки України Міністерство освіти і науки УкраїниЦентральноукраїнський державний педагогічний університет імені Володимира Винниченка Кафедра математики Тригонометричні рівняння. Їх види та способи розв’язування Виконала Студентка МА18М Фізико-математичного факультету Степанова А.М. м. Кропивницький, 2018 р. ЗМІСТ ВСТУП Розділ 1. Тригонометричні рівняння. Їх види та способи розв’язування 1.1 Означення тригонометричних рівнянь 1.2 Види тригонометричних рівнянь та способи їх розв’язування
Висновок Список використаної літератури ВСТУП
Тригонометрія - слово грецьке і в буквальному перекладі означає вимірювання трикутників ( - трикутник, - вимірюю). В даному випадку вимірювання трикутників слід розуміти як розв’язування трикутників, тобто визначення сторін, кутів та інших елементів трикутника, якщо дано лише деякі з них. Велика кількість практичних завдань, а також завдань планіметрії, стереометрії, астрономії та інших наводяться до задач розв’язування трикутників. Вперше способи розв’язування трикутників, засновані на відношеннях між сторонами і кутами трикутника, були знайдені давньогрецькими астрономами Гиппархом (2 ст. До н. Е..) і Клавдієм Птолемеєм (2 ст. Н. Е..). Пізніше такі відношення почали називати тригонометричними функціями. Значний внесок у розвиток тригонометрії внесли арабські вчені аль-Батанов (850-929) і Абуль-Вефа Мухамед-бен Мухамед (940-998), який склав таблиці синусів і тангенсів через 10' з точністю до 1/604. Теорему синусів уже знали індійський вчений Бхаскара та азербайджанський астроном і математик Насіреддін Тусі Мухамед. Теорему тангенсів довів Йоганн Мюллер (1436-1476). Довгий час тригонометрія носила чисто геометричний характер. Такою вона була ще і в середньовіччі. Поступово тригонометрія органічно увійшла в математичний аналіз, механіку, фізику і технічні дисципліни. Починаючи з XVII ст., тригонометричні функції почали застосовувати до розв’язування рівнянь, задач механіки, оптики, електрики, радіотехніки, розповсюдження хвиль, для вивчення змінного електричного струму тощо. Тому тригонометричні функції всебічно і глибоко досліджувалися . Знання графіків та властивостей тригонометричних функцій дозволяють знаходити розв’язки тригонометричних рівнянь. РОЗДІЛ 1 Тригонометричні рівняння. Їх види та способи розв’язування 1.1 Означення тригонометричних рівнянь Свого часу велася запекла дискусія з приводу означення поняття тригонометричне рівняння. Тригонометричним пропонували називати:
З цього приводу слід погодитись з думкою С. І. Новосьолова, який вважав, що розходження в означеннях тригонометричного рівняння не є принциповими. Важливо одне - немає загального методу розв'язування тригонометричних рівнянь. Слід наголосити на принциповій відмінності тригонометричних рівнянь від алгеб раїчних: тригонометричні рівняння, в яких змінна входить лише під знак тригонометричної функції, або зовсім не мають розв'яз ків, або мають їх безліч. Це пов'язано з властивістю періодичності тригонометричних функцій. 1.2 Види тригонометричних рівнянь та способи їх розв’язування Найпростіші тригонометричні рівняння Як правило, розв’язування тригонометричного рівняння зводиться до розв’язування рівнянь виду sin t = a, cos t = a, tg t = a, ctg t = a, які називають найпростішими. Способи розв’язування таких рівнянь детально вивчаються в курсі алгебри та початків аналізу 10-го класу. Зупинимось на більш складних видах тригонометричних рівнянь. Розв’язування тригонометричних рівнянь способом розкладанням на множники Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один зі співмножників дорівнює нулю, а інші при цьому не втрачають змісту. Розглянемо цей спосіб. Приклад. Розв’яжіть рівняння 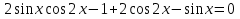 . .Розв’язання. Згрупуємо доданки у лівій частині рівняння: 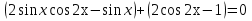 . .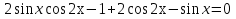 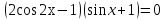 Враховуючи умову рівності нулю, маємо: 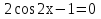 або або 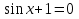 . . Кожне з цих рівнянь легко звести до найпростішого: 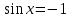 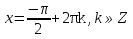 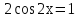 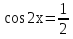 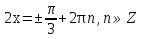 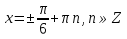 Відповідь: 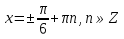 ; ;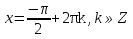 . .Розв’язування тригонометричних рівнянь, що зводяться до квадратних У курсі алгебри 8-го класу було вивчено способи розв’язування квадратних рівнянь, які використовуються і при розв’язуванні окремих випадків тригонометричних рівнянь. Приклад. Розв’яжіть рівняння 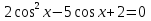 . .Розв’язання. Дане рівняння є квадратним відносно 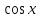 . Нехай . Нехай 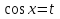 , де , де 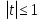 , тоді одержимо рівняння , тоді одержимо рівняння 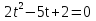 . Розв’язавши його, знайдемо . Розв’язавши його, знайдемо 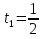 ; ; 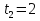 . Значення . Значення 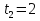 не задовольняє умову не задовольняє умову 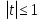 , отже: , отже: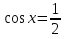 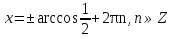 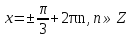 Відповідь: 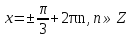 Розв’язування однорідних рівнянь Рівняння виду 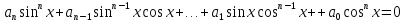 називається однорідним рівнянням n-го степеня відносно синуса і косинуса. Це такі рівняння, у яких ліва частина є многочленом, у кожному члені якого сума показників степенів синуса і косинуса одного і того самого аргументу однакова, а права – 0. однорідні рівняння n-го степеня відносно синуса і косинуса розв’язують діленням обох частин на називається однорідним рівнянням n-го степеня відносно синуса і косинуса. Це такі рівняння, у яких ліва частина є многочленом, у кожному члені якого сума показників степенів синуса і косинуса одного і того самого аргументу однакова, а права – 0. однорідні рівняння n-го степеня відносно синуса і косинуса розв’язують діленням обох частин на 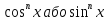 . Проте попередньо слід довести, що . Проте попередньо слід довести, що 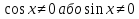 . .Однорідне тригонометричне рівняння 1-го степеня - це рівняння виду: 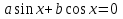 , де a і b , де a і b 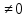 Приклад. Розв’яжіть рівняння 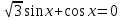 . .Розв’язання. Поділимо обидві частини рівняння на 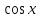 . Оскільки корені рівняння . Оскільки корені рівняння 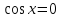 не є коренями вихідного рівняння, то не є коренями вихідного рівняння, то 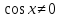 . Маємо: . Маємо: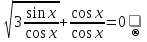 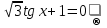 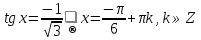 Відповідь: 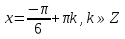 Однорідне тригонометричне рівняння 2-го степеня - це рівняння виду: 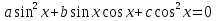 , де a, b і c , де a, b і c 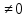 Приклад. Розв’яжіть рівняння 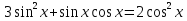 . .Розв’язання. 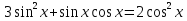 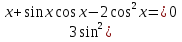 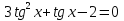 , тому що , тому що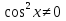 . .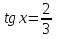 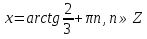 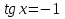 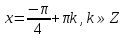 Відповідь: 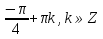 ; ; 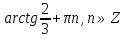 Однорідні тригонометричні рівняння n-го степеня розв’язуються аналогічно до вищеназваних. Розв’язування тригонометричних рівнянь виду 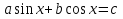 Тригонометричні рівняння можуть бути розв’язані за допомогою формул універсальної підстановки: 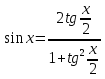 і і 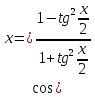 При цьому треба пам’ятати, що застосовуючи такі формули, ми звужуємо область допустимих значень рівняння, оскільки функція 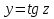 не існує при не існує при 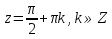 . .Приклад. Розв’яжіть рівняння 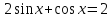 . .Розв’язання. Розв’яжемо дане рівняння за допомогою формул універсальної підстановки: 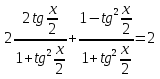 Перевіримо, чи будуть числа виду 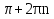 , , 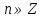 , коренями рівняння , коренями рівняння 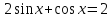 : :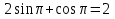 ; ;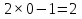 – неправильно. – неправильно.Отже, числа виду 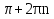 не є коренями даного рівняння. Нехай не є коренями даного рівняння. Нехай 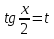 . Тоді . Тоді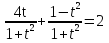 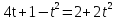 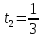 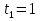 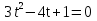 Повернемось до початкової змінної: 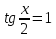 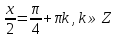 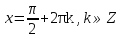 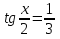 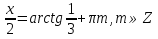 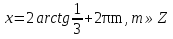 Відповідь: 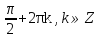 ; ; 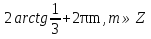 Рівняння, що розв’язуються за допомогою заміни 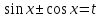 Зустрічаються такі тригонометричні рівняння, в яких доцільною є заміна 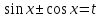 . Проте слід пам’ятати, що якщо . Проте слід пам’ятати, що якщо 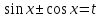 , то , то 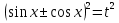 , ,  , тобто , тобто 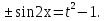 Приклад. Розв’яжіть рівняння 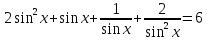 . .Розв’язання. ОДЗ: 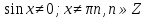 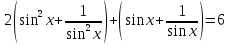 Нехай  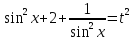 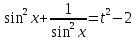 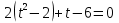 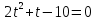 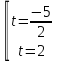 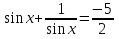 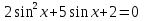 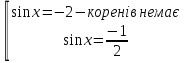 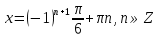 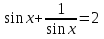 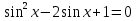 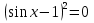 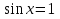 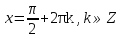 Відповідь: 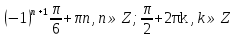 Розв’язування тригонометричних дробово-раціональних рівнянь Тригонометричні дробово-раціональні рівняння – це рівняння, що містять тригонометричні функції у знаменнику і зводяться до виду 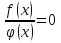 . Такі рівняння можуть містити, так звані, сторонні розв’язки. Сторонніх розв’язків позбуваються за допомогою врахування додаткових умов (знаменник дробу не може дорівнювати нулю). . Такі рівняння можуть містити, так звані, сторонні розв’язки. Сторонніх розв’язків позбуваються за допомогою врахування додаткових умов (знаменник дробу не може дорівнювати нулю).Приклад. Розв’яжіть рівняння 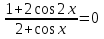 . .Розв’язання. Використавши умову, за якої дріб дорівнює 0, і те, що 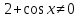 для будь-якого дійсного значення для будь-якого дійсного значення 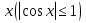 , маємо: , маємо: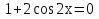 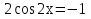 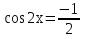 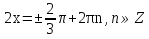 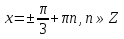 Відповідь: 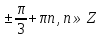 Графічний спосіб Приклад. Розв’яжіть рівняння 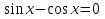 . .y 1 0 -1 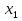 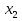 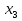 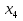 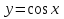 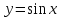 x Розв’язання. Запишемо дане рівняння у вигляді 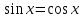 і введемо функції і введемо функції 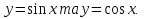 Побудувавши в одній системі координат графіки цих функцій, знайдемо розв’язки рівняння як абсциси точок перетину графіків. Побудувавши в одній системі координат графіки цих функцій, знайдемо розв’язки рівняння як абсциси точок перетину графіків.Відповідь: 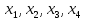 Тригонометричні рівняння, що містять ірраціональність Це тригонометричні рівняння, що містять в собі тригонометричну функцію під знаком радикала будь-якого степеня. Розв’язки рівняння такого типу обов’язково повинні перевірятись на їх належність ОДЗ рівняння. Приклад. Розв’яжіть рівняння 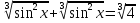 . .Розв’язання. ОДЗ: 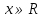 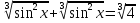 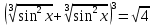 Застосуємо формулу 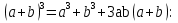 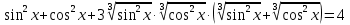 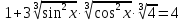 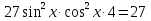 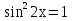 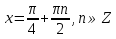 Відповідь: 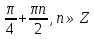 Тригонометричні рівняння з параметрами Рівняння з параметрами – це рівняння, до запису якого, крім змінної та числових коефіцієнтів входять також буквені коефіцієнти – параметри. Розв’язати тригонометричне рівняння з параметрами – значить для будь-якого припустимого значення параметра знайти множину всіх розв’язків даного рівняння. Таким чином розв’язання задач з параметром відрізняється від розв’язання аналогічної задачі без параметра, необхідністю дослідити всі можливі значення невідомого при всіх припустимих значеннях параметра. Приклад. Розв’яжіть рівняння 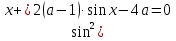 . .Розв’язання. Нехай 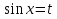 , , 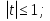 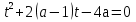 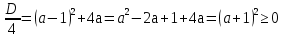 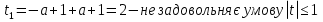 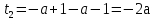 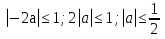 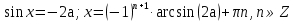 Відповідь:при 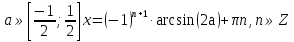 ВИСНОВОК Кут у геометрії – фігура, що утворена при повороті променя на площині навколо початкової точки. Тобто можна розглянути кут як алгебраїчну величину, яка може набувати як додатних, так і від’ємних значень. Але з чисто теоретичного поняття, кут швидко переріс у фізичну величину, яка вже давно використовується у науці і техніці. А отже, постійно потребує нових способів знаходження його величини. Поняття тригонометричної функції з’явилось саме завдяки необхідності наведеній вище. Тригонометрична функція – це функція кута, що особлива корисна при дослідження та моделюванні періодичних подій. «Функції, зокрема і тригонометричні, потрібні не лише натуралістові, без них тепер не обійдеться і соціологія. Взагалі, нині немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення»,- говорив К.Ф. Лебединцев. Тригонометричні функції можуть бути визначенні відношенням двох сторін прямокутного трикутника, координат точок кола, або більш загально – нескінченними рядами чи розв’язком диференційного рівняння. Широко застосовуються у всіх галузях людського життя, тому питання про розв’язування рівнянь, які містять змінну під знаком тригонометричної функції, досить актуальне у світі сучасних технологій. Адже «складання рівняння задачі є основним засобом застосування математики до природознавства і техніки. Без рівняння немає математики як засобу пізнання природи»,- вважав П. С. Александров. Під час розв’язування тригонометричних рівнянь варто пам’ятати про можливі випадки порушення рівносильності рівняння, тобто про втрату і появу сторонніх розв’язків. Та навіть при дотриманні алгоритму розв’язування тригонометричних рівнянь, у результаті розв’язування одного і того самого рівняння різними способами можна дістати різні загальні формули розв’язків цього рівняння. Їх еквівалентність можна довести, перетворивши формули та об’єднавши кілька формул в одну. Можна також довести рівність знайдених множин розв’язків, записавши в розгорнутому вигляді прогресії, n-м членом яких є формула розв’язку тригонометричного рівняння. Розглянутими типами тригонометричних рівнянь не вичерпується вся множина існуючих їх видів (способи піднесення до квадрата, введення допоміжного аргументу, зведення до однієї тригонометричної функції, оцінки лівої і правої частини рівняння, метод введення допоміжного кута, тригонометричні рівняння з модулями тощо). Існує багато методичної літератури, яка може стати в нагоді при досліджені методів розв’язування тригонометричних рівнянь. СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
|
