РГР. Тройки Хоара
 Скачать 10.82 Kb. Скачать 10.82 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тверской государственный университет» Факультет прикладной математики и кибернетики Направление: 09.03.03 — «Прикладная информатика» Расчётно-графическая работа по дисциплине «Теоретические основы информатики» Тема: «Тройки Хоара» Автор: студент 11-й группы Романов Даниил Денисович Проверил: к.ф.-м.н., Карлов Борис Николаевич Тверь — 2021 Вариант № 68 Написать структурированную программу и доказать её правильность методом Хоара. Проверить, можно ли из пятеричной записи числа x отбросить несколько первых цифр так, чтобы оно стало квадратом. Использовать s – прибавление 1, =, <, +, -, *, : - целочисленное деление, % - остаток от деления. Структурированная программа algorithm Five; arguments x; returns r; r = 0; z = x while z > 0 num = 0; while num < z do if num * num == z then r = 1; end; num = num + 1; end; tenX = z; fiveX = 0; n = 0; last = 0; while tenX > 4 do fiveX = fiveX * 10; last = tenX % 5 fiveX = fiveX + last; tenX = tenX / 5; n = n + 1; end; s = 0; while s < n do last = last * 5; s = s + 1; end; z = z - last; end; end; Ограничители и инварианты Первый внутренний цикл: Ограничитель: x – num. Инвариант: ( 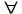 y) (y < x y) (y < x 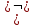 (y * y = x)) (y * y = x)) 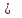 r rВторой внутренний цикл: Пусть S(x) – сумма цифр числа х Ограничитель: x Инвариант: S(tenX) + S(fiveX) Третий внутренний цикл: Ограничитель: n - s Инвариант: 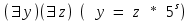 Внешний цикл: Пусть S(x, y) = 1, если х может быть получен из у откидыванием нескольких первых цифр в пятеричной системе счисления, 0 – иначе. Пусть P(x) = 1, если х – квадрат какого-либо числа. Ограничитель: x Инвариант: (∀y)(S(y, x) ∧¬S(z, y)∧ ¬y=z ∧ P(y)) |
