Кашникова И.В., Юферева О.Д. Экономико-математические методы и м. Практикум для студентов экономических специальностей всех форм обучения Минск 2004 удк ббк

• Название: Практикум для студентов экономических специальностей всех форм обучения Минск 2004 удк ббк
• Дата: 25.03.2019
• Размер: 0.74 Mb.
• Имя файла: Кашникова И.В., Юферева О.Д. Экономико-математические методы и м.doc
• Тип: Практикум; #71469
• страница: 1 из 7

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Белорусский государственный экономический университет


И.В. Кашникова, О. Д. Юферева


ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ

МЕТОДЫ И МОДЕЛИ

Лабораторный практикум

для студентов экономических специальностей

всех форм обучения

Минск 2004


УДК

ББК

Р е ц е н з е н т к.э.н, доцент Е.В. Крюк

Р е к о м е н д о в а н о кафедрой прикладной математики и экономической кибернетики

У т в е р ж д е н о Редакционно-издательским советом университета


Кашникова И.В., Юферева О.Д. Экономико-математические методы и модели в коммерческой деятельности. Лабораторный практикум. Для студентов ФЭУТ дневной формы обучения. – Мн.: БГЭУ, 2004. – 37 с.
УДК

ББК

ОГЛАВЛЕНИЕ

Предисловие……………………………………………………………….	4
Лабораторная работа № 1 «Оптимизация деятельности торгового предприятия»………………………………..…..	5
Лабораторная работа № 2 «Оптимизация сетевого графика по времени»……………………………………………………………………..	9
Лабораторная работа № 3 «Использование элементов теории игр при принятии управленческих решений» …………………………………….	18
Лабораторная работа №4 «Многономенклатурные модели управления запасами» ………………………………………………………………….	22
Лабораторная работа №5 «Балансовые модели в экономике»………….	28
Лабораторная работа №6 «Модели анализа инвестиционных проектов»	33
Рекомендуемая литература…………………………………………………	37

Предисловие
Математическое моделирование экономических процессов тесно связано с компьютеризацией экономической науки и ее практическим применением. Лабораторные занятия по курсу “Экономико-математические методы и модели” предназначены для углубления теоретические знаний студентов по моделированию экономических процессов как на микро так и на макро уровне, а также для получения практических навыков построения численных моделей, их реализации с применением ПЭВМ и анализа полученных результатов

Данный лабораторный практикум содержит варианты типовых заданий по лабораторным работам, выполнение которых предполагает использование ЭВМ и краткие инструкции для решения задач с использованием пакета EXCEL.

Лабораторная работа №1

Тема «Оптимизация деятельности торгового предприятия»

Цель - научить студентов:

• 
  составлять оптимизационные модели;
  
• 
  решать полученные математические задачи на ЭВМ с использованием пакета EXCEL;
  
• 
  проводить содержательный послеоптимизационный анализ полученных результатов.
  

Постановка задачи.

Торговое предприятие (предприятие оптовой торговли), исходя из специализации, может реализовать n групп товаров T_j (j=1,2,…n). Пусть общая площадь торговых залов P, P_j – норматив складских площадей на содержание товаров j-ой группы; R- фонд рабочего времени работников, r_j – плановый норматив затрат времени работников на единицу товарооборота j-ой товарной группы. Пусть B – допустимые издержки обращения, b_j – плановый норматив издержек обращения на единицу товарооборота j-ой товарной группы. S – общий объем товарных запасов. S_j – норматив товарных запасов на единицу товарооборота j-ой товарной группы. Q- плановый показатель товарооборота. q_j – параметр товарооборота (средняя цена реализации), по j-ой товарной группе. G_j – минимально допустимые значения плана товарооборота по j-ой товарной группе. C_j – торговая прибыль в расчете на единицу товарооборота j-й группы.

Требуется

1. 
   определить план хозяйственной деятельности торгового предприятия, обеспечивающий максимум торговой прибыли при заданных ограничениях на складские площади, трудовые ресурсы, издержки обращения, товарные запасы, величину товарооборота и др.
   
2. 
   Сделать анализ полученного решения.
   
3. 
   Дать экономическую интерпретацию двойственным оценкам и дополнительным двойственным переменным.
   
4. 
   Выявить «узкие места» на торговом предприятии и сделать рекомендации по их «расшивке»
   

	Номер варианта
	*	1	2	3	4	5	6	7	8	9
C1	120	40	60	50	100	80	130	90	110	70
C2	50	15	25	70	30	40	30	35	50	60
C3	30	10	15	20	80	20	10	20	10	15
C4	100	35	50	80	50	120	80	100	40	60
P	110000	60000	50000	65000	75000	80000	100000	160000	95000	110000
R	950000	400000	350000	480000	550000	500000	650000	250000	320000	640000
B	1200000	600000	720000	850000	800000	850000	1100000	330000	770000	900000
S	180000	90000	110000	150000	180000	180000	220000	96000	160000	220000
Q	150000	300000	510000	500000	450000	420000	710000	320000	350000	330000
P1	18	9	15	12	13	15	20	10	14	25
P2	26	13	16	20	21	20	27	30	20	32
P3	16	8	10	10	11	13	18	20	10	23
P4	10	5	1	12	14	11	12	15	15	15
R1	150	75	100	120	115	110	160	25	35	165
R2	140	70	90	100	95	90	150	70	80	155
R3	50	25	30	40	45	40	50	30	40	65
R4	80	40	60	50	60	55	90	40	50	85
B1	170	85	120	150	140	130	170	58	135	176
B2	230	115	200	190	180	170	200	92	185	205
B3	280	140	220	200	190	185	270	96	190	275
B4	120	60	90	110	100	105	130	55	110	134
S1	31	15	20	18	20	19	33	14	10	35
S2	42	21	35	30	30	32	45	20	30	48
S3	30	15	16	20	15	17	31	10	20	33
S4	20	10	18	12	10	11	22	16	15	24
Q1	200	100	160	120	115	117	210	70	75	120
Q2	150	75	110	90	85	80	165	80	85	90
Q3	170	85	100	130	125	120	180	120	125	60
Q4	50	25	80	60	50	45	60	50	50	45
G1	1200	600	1000	1100	1050	1000	1000	800	1020	500
G2	1000	500	800	850	800	900	1100	950	850	700
G3	1500	750	1200	1050	1000	750	1400	800	950	450
G4	1200	1100	1300	950	900	1100	1600	1000	800	600

Порядок выполнения работы. (на примере варианта *)

1. Составление математической модели задачи. Введем переменные: X_j (ед.)- величина товарооборота j-й товарной группы. Тогда математическая модель задачи примет вид: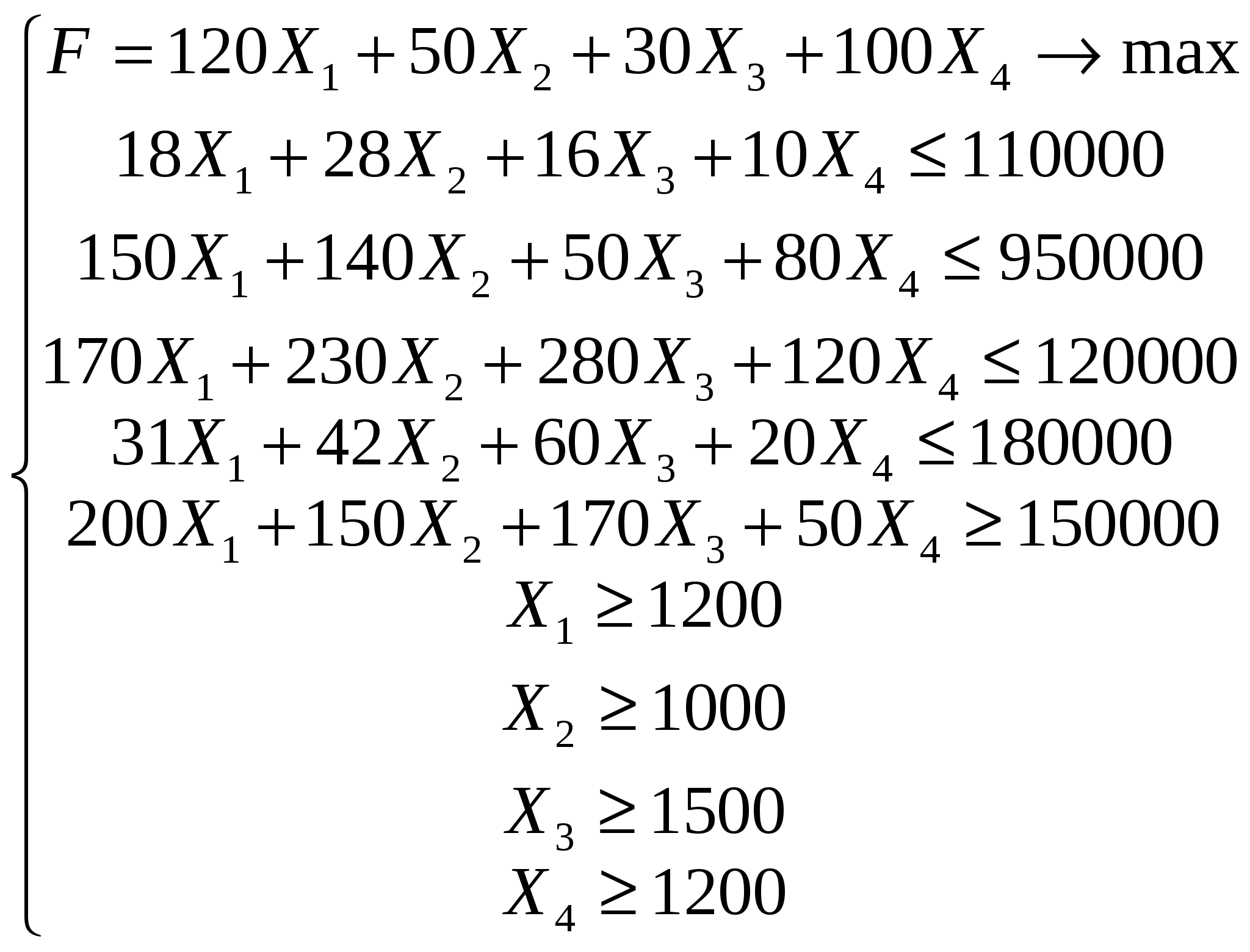



2. Инструкция по решению задачи средствами EXCEL.

1. 
   Ввод условий задачи.
   

Шаг 1. Сделать форму и ввести исходные данные.

	A	B	C	D	E	F	G	H
1			Переменные
2	Имя	X1	X2	X3	X4
3	значение
4	нижн.гр	1200	1000	1500	1200
5	верхн.гр
6
7	коэф.ЦФ	120	50	30	100
8			Ограничения
9	вид					лев.ч.	знак	прав.ч.
10	склад	18	26	16	10		<=	110000
11	трудов.	150	140	50	80		<=	950000
12	изд. обр.	170	230	280	120		<=	1200000
13	Запасы	31	42	60	20		<=	180000
14	товарооб.	200	150	170	50		>=	150000

Шаг 2. Ввод зависимостей из математической модели.

Чтобы получить значение целевой функции в ячейке F7, воспользуемся функцией СУММПРОИЗВ. Для этого поместим курсор в ячейку F7, с помощью команды МАСТЕР ФУНКЦИЙ вызовем математическую функцию СУММПРОИЗВ. На экране появится диалоговое окно. В массив 1 вводим строку со значениями переменных, т.е. $B$3:$E$3 (знак $ ставим для того, чтобы адрес не менялся при копировании формул). В массив 2 ввести адрес строки коэффициентов целевой функции, т.е. В7:Е7.

Заметим, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

Далее копируем формулу из ячейки F7 в столбец «Левые части ограничений».

2. 
   Решение задачи осуществляется в следующей последовательности.
   

Командой Поиск решения из меню Сервис откроем диалоговое окно Поиск решения и занесем в него необходимые данные:

Установить целевую функцию – адрес ячейки, отведенной под значение целевой функции, т.е. F7;

Равной – максимальному значению;

Изменяя ячейки – адреса изменяемых значений переменных, т.е. B3:E3;

Ограничения – Добавить…

На экране появится диалоговое окно Добавление ограничения. Здесь вводим граничные условия на переменные: В3:Е3  В4:Е4 Добавить.

Вводим ограничения по ресурсам:

F10 : F14  H10 : H14 ОК .

Далее командой Параметры вызываем диалоговое окно Параметры и устанавливаем флажки: Линейная модель, Неотрицательные значения, Автоматическое масштабирование. Возвращаемся в диалоговое окно Поиск решения и, щелкнув по кнопке Выполнить, находим оптимальное решение задачи. На экране появляется диалоговое окно Результаты поиска решения.

Помечаем для вывода все три отчета: по результатам, по устойчивости, по пределам.

2. 
   Анализ полученных результатов.
   

Лабораторная работа №2.

Тема. Оптимизация сетевого графика по времени

Цель Научиться решать задачу сетевого планирования с одновременной оптимизацией средствами EXCEL.

Постановка задачи 1.

Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность t_ij и минимально возможное время выполнения d_ij. Пусть задан срок выполнения проекта t₀, а расчетное t_кр > t_0. Продолжительность выполнения работы (i,j) линейно зависит от суммы дополнительно вложенных средств х_ij и выражается соотношением: t^’_ij = t_ij - k_ijx_ij. Технологические коэффициенты k_ij известны.

Требуется найти такие t ^н _ij, t^o_ij, x_ij, чтобы:

• 
  срок выполнения всего комплекса работ не превышал заданной величины t₀;
  

• 
  суммарное количество дополнительно вложенных средств было минимальным.;
  

• 
  продолжительность выполнения каждой работы t^’_ij была не меньше заданной величины d_ij.
  

Таблица 2.1

Но-мер задачи	Пара- метры	Работы										Срок выпол- нения проекта t0
		1,2	1,3	1,4	2,4	2,5	3,4	3,6	4,5	4,6	5,6
	tij	7	11	16	6	10	8	13	12	14	9
*	dij	4	8	13	5	7	6	10	10	11	7	34
	kij	0,1	0,3	0,2	0,05	0,25	0,2	0,12	0,5	0,08	0,02
	tij	9	12	18	8	12	5	12	10	13	12
1	dij	7	10	15	6	10	3	8	7	12	10	35
	kij	0,05	0,2	0,25	0,08	0,15	0,1	0,06	0,05	0,1	0,5
	tij	10	13	24	9	11	17	10	15	15	20
2	dij	5	9	11	6	9	12	7	13	13	15	56
	kij	0,08	0,25	0,1	0,15	0,3	0,2	0,08	0,4	0,2	0,1
	tij	6	13	20	9	14	16	15	10	17	13
3	dij	5	10	16	7	11	13	12	7	15	9	40
	kij	0,05	0,25	0,3	0,07	0,15	0,1	0,05	0,03	0,14	0,5
	tij	19	10	35	18	20	9	22	17	20	18
4	dij	16	5	25	13	15	6	17	13	16	14	60
	kij	0,25	0,07	0,1	0,2	0,13	0,15	0,06	0,4	0,2	0,1
	tij	6	15	26	7	11	10	11	12	13	17
5	dij	5	13	20	5	9	7	8	9	12	15	50
	kij	0,07	0,2	0,3	0,1	0,05	0,1	0,04	0,05	0,15	0,5

1 Запишем все данные на сетевой график и рассчитаем сроки свершения событий .

1

4

3

5

2

7;4

10;7

9;7

14;11

6;5

12;10

16;13

11;8

8;6

13;10

6


0


19

11

31







7


Расчеты показали, что срок выполнения проекта t_кр = 40, т.е. превышает директивный срок t₀ = 34.


40

2. Составление математической модели задачи.

Целевая функция имеет вид

f= х₁₂ + х₁₃ + х₁₄ + х₃₄ + х₃₅ + х₄₅ + х₁₄ + х₃₄ + х₃₅ + х₄₅ (min) .

Запишем ограничения задачи:

а) срок выполнения проекта не должен превышать t₀ = 34:

t^о₃₆  34; t^о₄₆  34; t^о₅₆  34;

б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:

t^о₁₂ - t ^н ₁₂  4; t^о₃₄ - t ^н ₃₄  6;

t^о₁₃ - t ^н ₁₃  8; t^о₃₆ - t ^н ₃₆  10;

t^о₁₄ - t ^н ₁₄  13; t^о₄₅ - t ^н ₄₅  10;

t^о₂₄ - t ^н ₂₄  5; t^о₄₆ - t ^н ₄₆  11;

t^о₂₅ - t ^н ₂₅  7; t^о₅₆ - t ^н ₅₆  7;

в) зависимость продолжительности работ от вложенных средств:

t^о₁₂ - t ^н ₁₂ = 7 - 0,1x₁₂; t^о₁₃ - t ^н ₁₃ = 11 - 0,3x₁₃;

t^о₁₄ - t ^н ₁₄ = 16 - 0,2x₁₄; t^о₂₄ - t ^н ₂₄ = 6 - 0,05x₂₄;

t^о₂₅ - t ^н ₂₅ = 10 - 0,25x₂₅ ; t^о₃₄ - t ^н ₃₄ = 8 - 0,2x₃₄;

t^о₃₆ - t ^н ₃₆ = 13 - 0,12x₃₆ ; t^о₄₅ - t ^н ₄₅ = 12 - 0,5x₄₅;

t^о₄₆ - t ^н ₄₆ = 14 - 0,08x₄₆ ; t^о₅₆ - t ^н ₅₆ = 9 - 0,02x₅₆;

г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:

t ^н ₁₂ = 0; t ^н ₁₃ = 0; t ^н₁₄ = 0;

t ^н ₂₄  t^о₁₂; t ^н ₂₅  t^о₁₂;

t ^н ₃₄  t^о₁₃; t ^н ₃₆  t^о₁₃;

t ^н ₄₅  t^о₁₄; t ^н ₄₅  t^о₂₄;

t ^н ₄₅  t^о₃₄;

t ^н ₄₆  t^о₁₄; t ^н ₄₆  t^о₂₄;

t ^н ₄₆  t^о₃₄;

t ^н ₅₆  t^о₂₅; t ^н ₅₆  t^о₄₅;

д) условие неотрицательности неизвестных:

t ^н _ij  0, t^о_ij  0, x_ij  0, (i,j)  .

3. 
   Численное решение задачи: