Кашникова И.В., Юферева О.Д. Экономико-математические методы и м. Практикум для студентов экономических специальностей всех форм обучения Минск 2004 удк ббк

• Название: Практикум для студентов экономических специальностей всех форм обучения Минск 2004 удк ббк
• Дата: 25.03.2019
• Размер: 0.74 Mb.
• Имя файла: Кашникова И.В., Юферева О.Д. Экономико-математические методы и м.doc
• Тип: Практикум; #71469
• страница: 3 из 7

34



25

15

0


6

8

3. 
   Анализ полученных результатов. Чтобы выполнить работы проекта за директивное время t₀=34, необходимо дополнительно вложить 24 ден.ед. При этом средства распределятся следующим образом: 10 ден.ед. – в работу (1,3), 5 ден.ед. – в работу (1,4), 5 ден.ед. – в работу (3,4) и 4 ден.ед. – в работу (4,5), что приведет к сокращению продолжительности работы (1,3) на 3 дня, работы (1,4) - на 1 день, работы (3,4) - на 1 день и работы (4,5) - на 2 дня. Сокращение срока реализации проекта за счет вложения дополнительных средств составит 6 ед. времени.
   

Постановка задачи 2.

Проект представлен сетевым графиком. Для каждой работы известна ее продолжительность t_ij и минимально возможное время выполнения d_ij. Для сокращения срока реализации проекта выделено В ден.ед. Вложение дополнительных средств х_ij в работу (i,j) сокращает время ее выполнения до t^’_ij = t_ij - k_ijx_ij. Технологические коэффициенты k_ij известны.

Требуется найти такие t ^н _ij, t^o_ij, x_ij, чтобы:

• 
  время выполнения всего комплекса работ было минимальным;
  

• 
  количество используемых дополнительных средств не превышало B ден. ед.;
  

• 
  продолжительность выполнения каждой работы была не меньше заданной величины d_ij.
  

Таблица 2.3

Ва-ри- ант	Пара- метры	Работы							Сумма
		(1,2)	(1,3)	(1,4)	(2,3)	(3,4)	(3,5)	(4,5)	средств В
	tij	5	6	2	4	9	7	4
*	dij	3	4	1	2	5	4	2	47
	kij	0,5	0,2	0,3	0,25	0,4	0,2	0,1
	tij	10	18	16	12	7	13	11
1	dij	7	14	12	10	5	9	8	42
	kij	0,5	0,1	0,25	0,4	0,2	0,15	0,3
	tij	9	18	21	7	12	19	20
2	dij	6	14	18	4	9	15	16	33
	kij	0,2	0,25	0,15	0,4	0,3	0,12	0,2
	tij	15	8	7	5	13	11	7
3	dij	12	5	4	3	10	8	4	47
	kij	0,25	0,2	0,15	0,1	0,3	0,4	0,2
	tij	13	22	19	17	10	25	12
4	dij	10	18	15	14	7	21	9	49
	kij	0,3	0,1	0,05	0,2	0,4	0,2	0,25
	tij	16	12	10	8	3	9	11
5	dij	10	7	6	5	2	7	9	29
	kij	0,2	0,1	0,16	0,3	0,25	0,1	0,4

Решение варианта *.

1. Запишем все данные на сетевой график.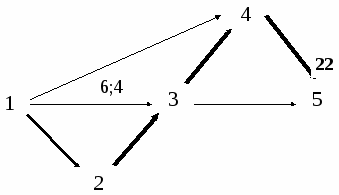



2;1 4;2

9;5


4;2
7;4

5;3



По первоначальному условию t_кр = 22 , т.е. проект может быть выполнен за 22 ед. времени.

2. Составление математической модели задачи.

Чтобы однозначно записать целевую функцию, добавим на сетевом графике фиктивную работу (5,6).


4


2;1 4;2

9;5


1

3

5

6
6;4 7;4




2

4;2
5;3


Целевая функция имеет вид t_кр = t^о₅₆ (min) .

Запишем ограничения задачи:

а) сумма вложенных средств не должна превышать их наличного количества:

х₁₂ + х₁₃ + х₁₄ + х₂₃ + х₃₄ + х₃₅ + х₄₅  47;

б) продолжительность выполнения каждой работы должна быть не меньше минимально возможного времени:

t^о₁₂ - t ^н ₁₂  3; t^о₃₄ - t ^н ₃₄  5;

t^о₁₃ - t ^н ₁₃  4; t^о₃₅ - t ^н ₃₅  4;

t^о₁₄ - t ^н ₁₄  1; t^о₄₅ - t ^н ₄₅  2;

t^о₂₃ - t ^н ₂₃  2; t^о₅₆ - t ^н ₅₆ = 0;

в) зависимость продолжительности работ от вложенных средств:

t^о₁₂ - t ^н ₁₂ = 5 - 0,5x₁₂; t^о₁₃ - t ^н ₁₃ = 6 - 0,2x₁₃;

t^о₁₄ - t ^н ₁₄ = 2 - 0,3x₁₄; t^о₂₃ - t ^н ₂₃ = 4 - 0,25x₂₃;

t^о₃₄ - t ^н ₃₄ = 9 - 0,4x₃₄; t^о₃₅ - t ^н ₃₅ = 7 - 0,2x₃₅ ;

t^о₄₅ - t ^н ₄₅ = 4 - 0,1x₄₅;

г) время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующей ей работы:

t ^н ₁₂ = 0; t ^н ₁₃ = 0; t ^н₁₄ = 0;

t ^н ₂₃  t^о₁₂;

t ^н ₃₄  t^о₁₃; t ^н ₃₄  t^о₂₃;

t ^н ₃₅  t^о₁₃; t ^н ₃₅  t^о₂₃;

t ^н ₄₅  t^о₁₄; t ^н ₄₅  t^о₃₄;

t ^н ₅₆  t^о₃₅; t ^н ₅₆  t^о₄₅;

д) условие неотрицательности неизвестных:

t ^н _ij  0, t^о_ij  0, x_ij  0, (i,j)  .

3. 
   Численное решение задачи: