Кашникова И.В., Юферева О.Д. Экономико-математические методы и м. Практикум для студентов экономических специальностей всех форм обучения Минск 2004 удк ббк
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
Табличную запись математической модели см. табл.2.4.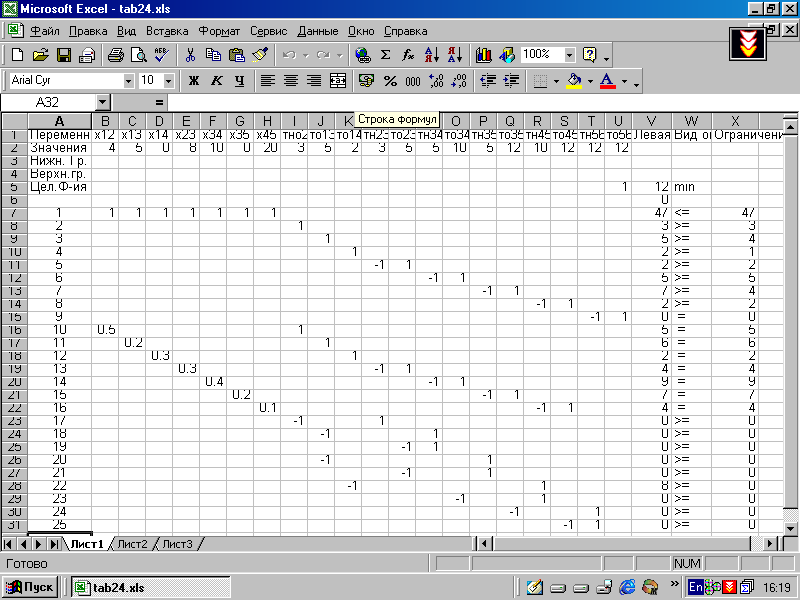 Решив данную задачу средствами EXCEL, получаем следующие результаты: t н12 = 0; tо12 = 3; t н13 = 0; tо13 = 3; t н14 = 0 ; tо14 = 2; t н 23 = 3; tо23 = 3; t н 34 = 3; tо34 = 8; t н 35 = 3; tо35 = 10; t н45 = 8; tо45 = 10; t н 56 = 10; tо56 = 10; x12 = 20; x13 = 0; x23 = 0; x14 = 0; x34 = 10; x35 = 0; x45 =20, tкр = 10. Результаты представим на сетевом графике:        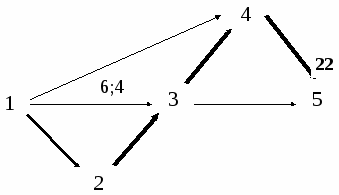 2;1 4;2  9;5 9;5  4;2 7;4  5;3 5;3 5. Анализ полученных результатов. При дополнительном вложении 47 ден.ед., проект может быть выполнен за 10 ед. времени. При этом средства распределятся следующим образом: 20 ден.ед. – в работу (1,2), 10 ден.ед. – в работу (3,4) и 20 ден.ед. – в работу (4,5), что приведет к сокращению продолжительности работы (1,2). Сокращение срока реализации проекта за счет вложения дополнительных средств составит 8 ед. времени. Лабораторная работа №3. Тема. «Применение элементов теории игр при принятии управленческих решений» Цель. Используя математический аппарат теории игр определить оптимальное количество продаваемого товара для максимизации среднего денежного дохода Постановка задачи. На каждой из двух торговых баз ассортиментный минимум составляет один и тот же набор из n видов товаров. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар, отличный от товара, завезенного в магазин В, то товар будет пользоваться спросом и магазин А от его реализации получит прибыль сj денежных единиц. Если же в магазины А и В завезены товары одинакового вида, то товар в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по хранению и возможно порче товара в размере di денежных единиц. Требуется формализовать конфликтную ситуацию, построить матрицу игры и дать рекомендации по выбору оптимальной смешанной стратегии при следующих числовых данных: n=4;
Порядок выполнения работы (на примере варианта*)
У руководства магазина А четыре стратегии: Ai - продавать товар i-ого вида (i=1,4). Аналогично у руководства магазина В стратегии Вj - продавать товар j-ого вида (j=1,4). Платежная матрица данной игры примет вид:
Определим, имеет ли игра оптимальное решение в чистых стратегиях. Для этого рассчитаем верхнюю и нижнюю чистые цены игры.
Итак, Так как , то игра не имеет решения в чистых стратегиях. 2. Найдем решение игры в смешанных стратегиях. 2.1. Чтобы свести игру к паре двойственных задач линейного программирования, увеличим все элементы платежной матрицы на 20:
Задача линейного программирования для игрока А: 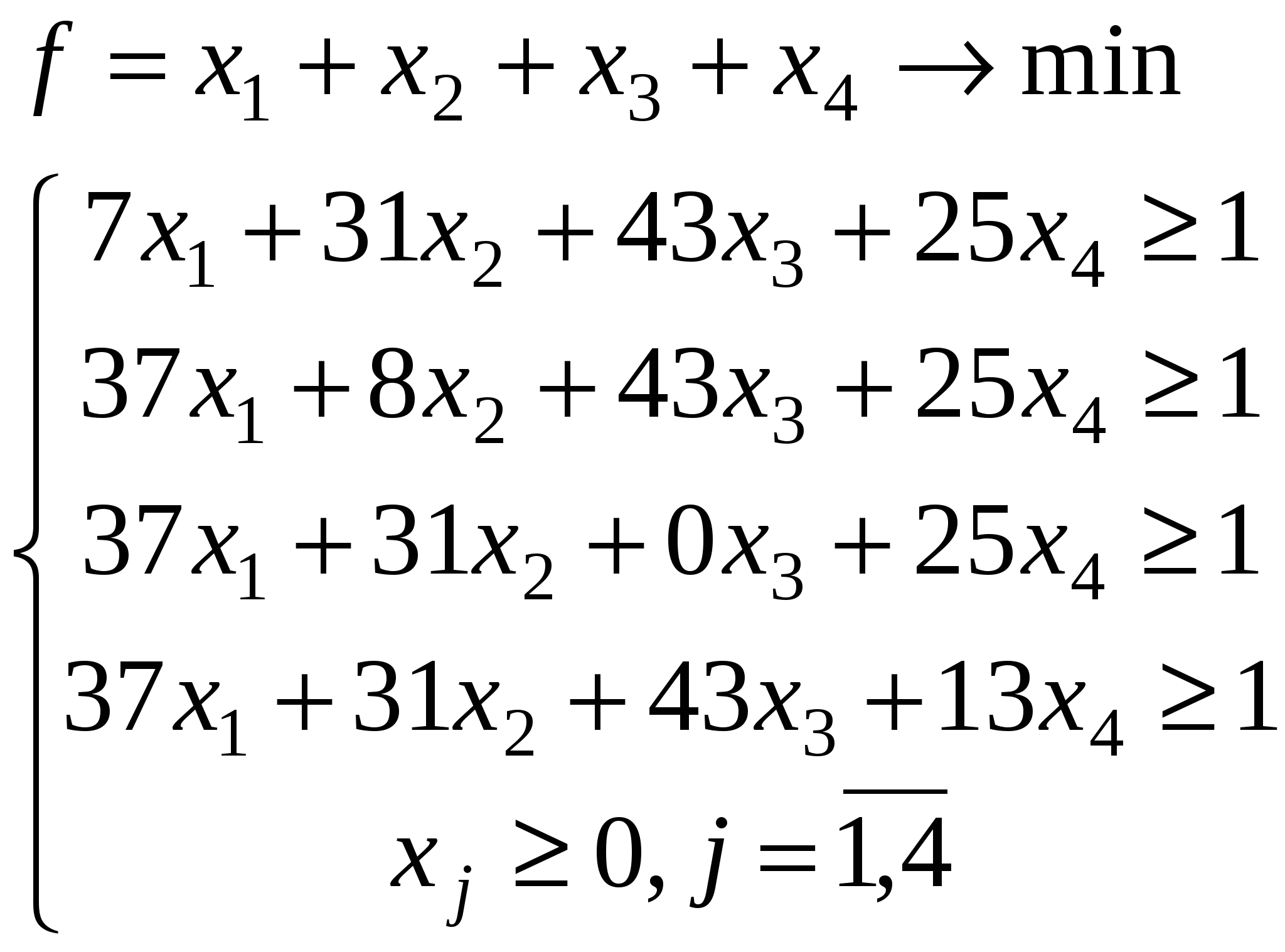 2.2. Численное решение задачи. Решив данную задачу средствами EXCEL, получаем: x1=0.016, x2=0.0073 x4=0.0167 fmin=0,04 Для определения смешанной стратегии, воспользуемся формулами: Отсюда смешанная стратегия : p=(0.4,0.182,0.418,0) V=5
Итак, оптимальной стратегией магазина А будет продажа товаров в следующей пропорции: 40% товара1; 18,2% товара 2; 41,8% товара 3; Средняя прибыль составит 5 д.е. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 4
4