туынды. туынды лекция. Туындыны анытамасы
 Скачать 49.19 Kb. Скачать 49.19 Kb.
|
|
Туындының анықтамасы Функцияны қарапайым қозғалыстар, құбылыстар мен процестердің математикалык моделі тұрғысынан қарастыру мақсатында қолданады. 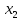 - - 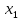 айырымын аргументтің айырымын аргументтің 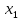 нүктесіндегі өсімшесі деп атайды. нүктесіндегі өсімшесі деп атайды.Алдымен аргумент және функция өсімшелері ұғымдарын анықтап алайық. Үзіліссіз y = f(x) функциясы берілсін. Аргументтің 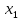 және және 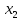 мәндері функцияның анықталу облысынан алынсын. мәндері функцияның анықталу облысынан алынсын.Өсімше  танбасымен белгіленіп, "дельта икс" деп оқылады. танбасымен белгіленіп, "дельта икс" деп оқылады. Функцияның аргументі 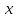 -ке -ке  өсімшесін берейік. өсімшесін берейік.  өсімшесін қабылдағаннан кейін аргументтің мәні өсімшесін қабылдағаннан кейін аргументтің мәні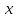 + +  болады. Өсімшенің таңбасы оң да, теріс те болуы мүмкін. Егер болады. Өсімшенің таңбасы оң да, теріс те болуы мүмкін. Егер  >0 болса, онда >0 болса, онда 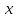 + + нүктесі нүктесі 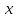 нүктесінің оң жағына, нүктесінің оң жағына,  < 0 болса, онда < 0 болса, онда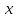 + +  нүктесі нүктесі 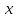 нүктесінің сол жағына орналасады (50-сурет). нүктесінің сол жағына орналасады (50-сурет). < 0 < 0  >0 >0 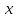 + +  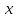 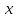 + +  50-сурет Сонымен, аргумент өсімшесін 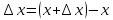 теңдігімен өрнектеуге болады. (1) Демек, аргументтің өсімшесі оның екі нүктедегі мәндерінің айырымына тең. Аргумент 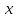 -ке -ке  өсімшесін бергенде у=f(x) функциясы да өcімше қабылдайды. Бұл функцияның есімшесі өсімшесін бергенде у=f(x) функциясы да өcімше қабылдайды. Бұл функцияның есімшесі 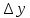 деп белгіленіп, деп белгіленіп,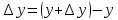 немесе 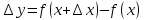 теңдігімен анықталады. (2) Сонда функция өсімшесі функцияның екі нүктедегі мәндерінің айырымына тең. МЫСАЛ. 1. 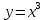 функциясының аргументі функциясының аргументі 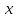 мәнінен мәнінен 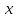 + + мәніне ауысқандағы өсімшесін табайық. мәніне ауысқандағы өсімшесін табайық. Шешуі. 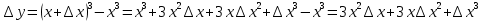 Сонымен, 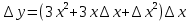 Функцияның туындысының анықтамасын берейік. Ол үшін функция өсімшесін аргумент өсімшесіне бөлеміз: 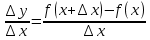 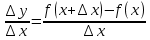 өрнегінің аргумент өсімшесі өрнегінің аргумент өсімшесі 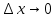 ұмтылғандағы шегі бар болса, онда ол шекті ұмтылғандағы шегі бар болса, онда ол шекті 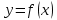 функциясының х нүктесіндегі туындысы деп атайды. функциясының х нүктесіндегі туындысы деп атайды.(3) Туындының белгіленуі: 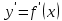 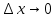 ұмтылғанда ұмтылғанда 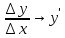 немесе немесе 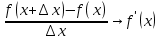 (4) (4)Оқылуы: 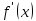 — “х-тен эф штрих”. — “х-тен эф штрих”.Функцияның туындысын табу амалын функцияны дифференциалдау деп атайды. хнүктесіндефункцияныңтуындысыбарболса, онда f(x) функциясыносынүктедедифференциалданатынфункциядепатайды. Егерфункцияаралықтыңбарлықнүктелеріндедифференциалданатынболса, ондаоныаралықтадифференциалданатынфункциядепатайды. y=f(x) функциясының 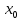 нүктесінде туындысы бар болса, онда осы нүктеде функция үзіліссіз болады. Кері тұжырым барлық жағдайда дұрыс бола бермейді. нүктесінде туындысы бар болса, онда осы нүктеде функция үзіліссіз болады. Кері тұжырым барлық жағдайда дұрыс бола бермейді.АЛГОРИТМ. Анықтама бойынша туынды табу алгоритмі: 1) аргументке 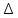 х өсімшесін беру; х өсімшесін беру;2) 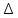 х өсімшеге сәйкес х өсімшеге сәйкес 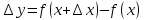 функция өсімшесін анықтау; функция өсімшесін анықтау; 3) функция өсімшесінің аргумент өсімшесіне қатынасын табу, яғни 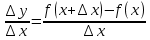 4) аргумент өсімшесі 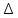 х нөлге ұмтылғандағы қатынастың шеrін яғни х нөлге ұмтылғандағы қатынастың шеrін яғни 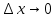 жағдайдағы жағдайдағы 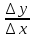 мәнін табу. мәнін табу.Алгоритмді қолданып, туынды табуға мысалдар қарастырайық. МЫСАЛ 2. a) 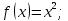 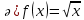 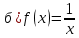 функциясының х нүктесіндегі туындысын табайық. функциясының х нүктесіндегі туындысын табайық.Шешуі: а) 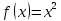 функциясынын туындысын табайык. Алгоритм бойынша: функциясынын туындысын табайык. Алгоритм бойынша: 1) х + 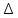 х; х; 2) 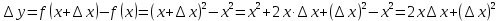 3) 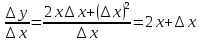 4) 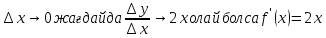 яғни яғни 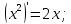 ә) 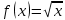 функциясының туындысын табайық. Алгоритм бойынша: функциясының туындысын табайық. Алгоритм бойынша:1) ) х + 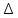 х; х;2) 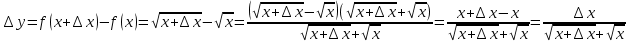 3) 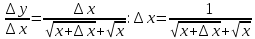 4) 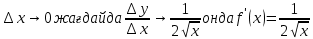 яғни яғни 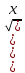 б) f(x)= 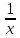 функциясының туындысын табайық. Алгоритм бойынша: функциясының туындысын табайық. Алгоритм бойынша:1) ) х + 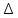 х; х;2) 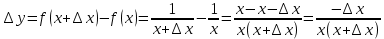 3) 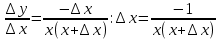 4) 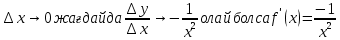 яғни яғни 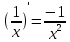 Осы қарастырылған мысалдардан мына қорытындыны аламыз: 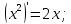 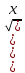 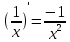 Жауабы: а) 2x; ә) 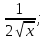 в) в) 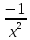 Тура осылай f(x) = С (С — тұрақты) және f(x) =х функцияларынын туындылары сәйкесінше C’ = 0, (x)’ = 1 болады. Сұрақтар: 1. Аргумент пен функцияның өсімшелері арасында кандай байланыс бар? Жауабын түсіндіріңдер. 2. Функцияның нүктедегі және аралықтағы дифференциалдануы деген ұғымдардың айырмашылығы неде? 3. Функцияның нүктедегі дифференциалдануы мен үзіліссіздігінің арасындағы байланысты қалай түсіндіруге болады? Жаттығулар A 13.1. f(x) функциясының 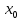 нүктесіндегі өсімшесін табыңдар: нүктесіндегі өсімшесін табыңдар:а) f(x) = 1 + 2х, 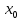 = 4, = 4,  = 0,01; = 0,01; ә) f(x) = -5х + 1,6, 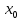 = -5, = -5,  = -0,1; = -0,1;6) f(х) = 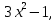 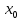 = 2, = 2,  =0,1 =0,1в) f(х) = 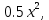 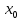 = -3, = -3,  =-0.3 =-0.313.2. а) Тіктөртбұрыштың қабырғалары 5 см және 12 см. Оның енін 0,8 см-ге, ұзындығын 0,6 см-ге арттырған кездегі тіктөртбұрыштың периметрі мен ауданының өсімшесін анықтаңдар. ө) Тіктөртбұрышты үшбұрыштың катеттері 3 см, 4 см. Егер катеттерін сәйкесінше 0,4 см және 0,2 см-ге арттырса, оның ауданының өсімшесі кандай болады? 13.3. Функцияның 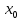 нүктесіндегі нүктесіндегі  және және 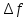 өсімшелерін табыңдар: өсімшелерін табыңдар: а) f(x)=cosx, 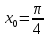 , , 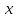 = =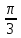 ә) f(x)= tgx, 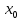 = = 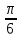 , , 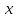 = =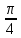 В 13.4. f(x) функциясының 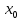 нүктесіндегі өсімшесін нүктесіндегі өсімшесін  және және 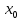 аркылы өрнектеңдер: аркылы өрнектеңдер: а) f(x) = 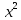 + x; ә) f(x) = + x; ә) f(x) =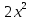 - x; - x;13.5. Алгоритмді пайдаланып, f(x) функциясының 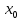 нүктесіндегі туындысын табыңдар: нүктесіндегі туындысын табыңдар:а) f(х) = 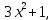 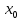 =- 2, =- 2,  ә) f(х) = ә) f(х) =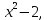 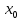 = -1, = -1,  13.6. Функцияның 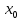 нүктесіндегі нүктесіндегі  және және 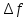 өсімшелерін табыңдар: өсімшелерін табыңдар:а) f(x)= 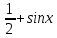 , , 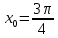 , , 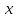 = =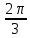 ә) f(x)= ctgx- 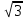 , , 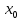 = = 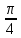 , , 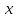 = =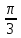 13.7. Функцияның аргументі  өсімшесін қабылдағанда өсімшесін қабылдағанда  -ге тең. Функцияның өсімшесін табындар: -ге тең. Функцияның өсімшесін табындар: а) f(x) =  , ,  = 0,29, = 0,29, = 2,25; = 2,25;ә) f(x) =  , ,  = 0,25, = 0,25, 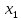 = 1,69. = 1,69.13.8. Бір елдің тұрғындарының саны t уақытында f(t)-ға тең. 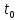 -ден -ден 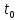 + + 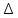 t дейінгі уақыт аралығындағы функцияның өсімшесінің мағынасы қандай болады? t дейінгі уақыт аралығындағы функцияның өсімшесінің мағынасы қандай болады?13.9. Сырықтың сол жақ шетінен х қашықтықтағы нүктенің температурасы f(x)-қа тең.  нүктесі нүктесі  + + х нүктесіне ауысқанда f(x) функциясы өсімшесінің физикалық мағынасы қандай? х нүктесіне ауысқанда f(x) функциясы өсімшесінің физикалық мағынасы қандай?Туындыны табу ережелері  1-ереже. Егер x нүктесінде  және және  функцияларының функцияларының  туындылары бар болса, онда осы нүктеде олардың қосындыларының да туындысы бар болады және ол туындылары бар болса, онда осы нүктеде олардың қосындыларының да туындысы бар болады және ол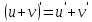 (1) (1)формуласымен анықталады. \ (u + vy - u' + v формуласымен анықталады. және 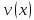 функцияларының х нүктесіндегі мәндерін қысқаша былай белгілейік: функцияларының х нүктесіндегі мәндерін қысқаша былай белгілейік: 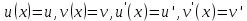 2-ереже. Егер x нүктесінде 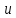 және және 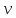 функцияларының функцияларының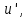 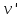 туындылары бар болса, онда осы нүктеде олардың айырымдарының туындысы бар болады және ол туындылары бар болса, онда осы нүктеде олардың айырымдарының туындысы бар болады және ол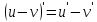 (2) (2)формуласымен анықталады. (2) формуласымен анықталады. Дәлелдеуі. Дәлелдеу үшін туындының анықтамасы мен туындыны табу алгоритмін қолданамыз. Ол үшін екі функцияның қосындысы 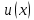 + + 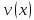 = F(x) функциясын алайық және аргумент х-ке = F(x) функциясын алайық және аргумент х-ке  өсімшесін берейік. Сонда өсімшесін берейік. Сонда 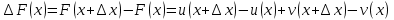 аламыз. Функцияның өсімшесін аргументтің өсімшесі аламыз. Функцияның өсімшесін аргументтің өсімшесі  -ке белсек, -ке белсек,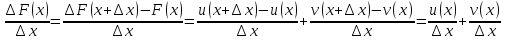 Енді 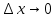 функцияның шегін табамыз және туындының анықтамасы бойынша F’(x)= функцияның шегін табамыз және туындының анықтамасы бойынша F’(x)=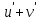 аламыз. Сонда аламыз. Сонда 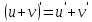 МЫСАЛ 1. f(x) = 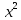 – x +5 функциясының туындысын табайық. – x +5 функциясының туындысын табайық.Шешуі. f ‘(х) = ( 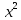 – x + 5)’ = ( – x + 5)’ = (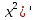 - (x)’ + (5)’ = 2х – 1 + 0 = 2х - 1. - (x)’ + (5)’ = 2х – 1 + 0 = 2х - 1.Жауабы: 2х - 1. ТҮСІНДІРІҢДЕР (10 +x- 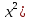 ’+y=1 - 2x функциясының туындысы қалай табылған? ’+y=1 - 2x функциясының туындысы қалай табылған?3-ереже. Егер x нүктесінде 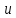 және және 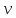 функцияларының функцияларының туындылары бар болса, онда осы нүктеде олардың көбейтінділерінің де туындысы бар болады және ол туындылары бар болса, онда осы нүктеде олардың көбейтінділерінің де туындысы бар болады және ол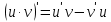 (3) (3)формуласымен анықталады. (2) формуласымен анықталады. Салдар. Егер 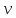 функциясының х нүктесінде туындысы бар, ал C түрақты сан болса, онда С функциясының х нүктесінде туындысы бар, ал C түрақты сан болса, онда С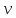 функциясының да осы х нуктесінде туындысы бар және ол функциясының да осы х нуктесінде туындысы бар және ол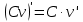 (4) (4)формуласымен анықталады. МЫСАЛ. 2. y=15 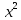 функциясының туындысын табайық. функциясының туындысын табайық. Шешуі: Мүндағы С=15, 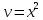 демек, (4) формуланы пайдаланамыз: демек, (4) формуланы пайдаланамыз:y’= (15 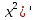 =15 =15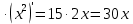 Жауабы: 30х. ТҮСІНДІРІҢДЕР у= 6 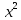 - 3x +1 функциясының туындысы 12х – 3 болатынын түсіндіріңдер. - 3x +1 функциясының туындысы 12х – 3 болатынын түсіндіріңдер.4-ереже. Егер x нүктесінде 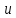 және және 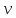 функцияларының функцияларының туындылары бар болса және туындылары бар болса және 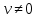 болса, онда осы нүктеде олардың бөліндісінің де туындысы бар болады және ол болса, онда осы нүктеде олардың бөліндісінің де туындысы бар болады және ол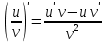 (5) (5)формуласымен анықталады. (2) формуласымен анықталады. МЫСАЛ. 3. 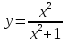 функциясының туындысын есептейік. функциясының туындысын есептейік.Шешуі: 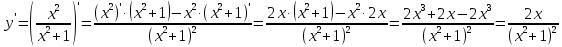 Жауабы: 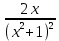 1-ден үлкен кез келген 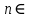 N үшін у = N үшін у = 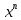 дәрежелік функцияныңтуындысы дәрежелік функцияныңтуындысы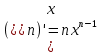 (6) (6)формуласымен есептелінеді. МЫСАЛ 4. а) у = 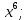 ә) у = 5 ә) у = 5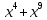 ; б) у = ; б) у =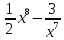 функцияларының туындысын табайық. функцияларының туындысын табайық.Шешуі. а) 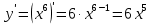 ә) 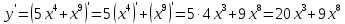 6) 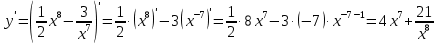 Жауабы: а 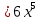 ; ә) ; ә)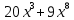 ; б) ; б)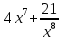 Сұрақтар: 1. Қосылғыштарының саны екіден артық болатын қосындының туындысын қалай табуға болады? 2. Бөліндінің туындысын есептегенде қандай шарт орындалуы тиіс? 3. Бөліндінің туындысын екі функцияның көбейтіндісінің туындысы ретінде қарастыруға бола ма? Жаттығулар A 14.1. Функциялардың туындысын табыңдар: а) 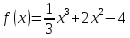 ә) ә) 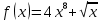 б) 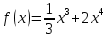 в) в) 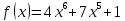 г) 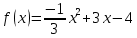 ғ) ғ) 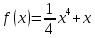 д) 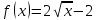 е) е) 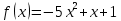 14.2. f '(х) = 0 тендеуін шешіңдер: а) f(x) = 4 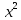 + 2x; ә) f(x) = 3 + 2x; ә) f(x) = 3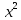 - 4x; - 4x;б) f(x) = 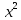 +х – 1; в) f(x) = -0.5 +х – 1; в) f(x) = -0.5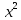 -4x+0.1; -4x+0.1;14.3. y = f(x) функцияларының 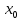 нүктесіндегі туындысын табыңдар: нүктесіндегі туындысын табыңдар:а) f(x) = 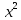 (х - 1), (х - 1), 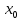 =-1; ә) =-1; ә)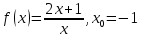 б) f(x) = 3х (х + 1), 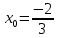 в) в)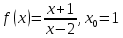 14.4. f ‘(x) > 0 теңсіздігін шешіңдер: а) f(x) = 18 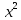 - 7х + 1; ә) - 7х + 1; ә)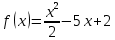 б) 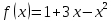 в) в) 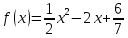 14.5. Функциялардың туындысын табындар: а) f(x) = (х + 5)(х – 4); ә) f(x) = 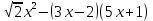 б) f(x) = 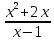 в) f(x)= 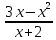 B 14.6. Функциялардың туындысын табыңдар: а) 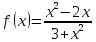 ә) ә)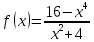 б) 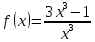 в) в)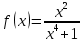 14.7. f(x) функциясының 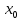 нүктесіндегі туындысының мәнін есептеңдер: нүктесіндегі туындысының мәнін есептеңдер:а) f(x) = 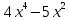 , , 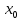 =1; =1; ә) f(x) = 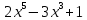 , , 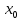 =-2; =-2; 14.8. y = f(x) функциясының х = -1 болғандағы туындысының мәнін табындар: а) 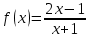 ә) ә)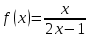 б) 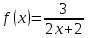 в) в)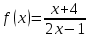 14.9. f '(х) = 0 теңдеуін шешіңдер: а) f(x) = 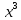 + 3 + 3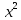 + 3x + 1; + 3x + 1; ә) f(x) = 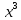 – 6 – 6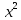 + 12х-1. + 12х-1.14.10. f '(х) > 0 теңсіздігін шешіңдер: а) f(x) = 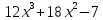 , ,  ә) f(x) = 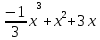 14.11. f ’(x) 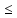 0 теңсіздігін шешіңдер: 0 теңсіздігін шешіңдер:а) f(x) = 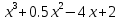 ə) f(x) = 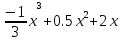 14.12. Егер f(x) 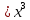 + 2 + 2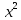 - 3x және g(x) = - 3x және g(x) = 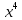 -3 -3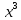 – 3х болса, онда f '(0) және g'(0) мәндерін салыстырыңдар. – 3х болса, онда f '(0) және g'(0) мәндерін салыстырыңдар. |
