Расчётно-графическая работа надёжность ис. РГР НадИС. Тверской государственный технический университет (Твгту) Кафедра информационных систем и технологий Дисциплина Надежность Информационных Систем
 Скачать 99.74 Kb. Скачать 99.74 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тверской государственный технический университет» (ТвГТУ) Кафедра информационных систем и технологий Дисциплина «Надежность Информационных Систем» РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА Вариант 2 Студент: Комиссаров А.К. Форма обучения: заочная Группа: Б.ИСТ.ИСАУ.18.35 Руководитель: Палюх Борис Васильевич Тверь, 2022г. Таблица 1- Исходные данные
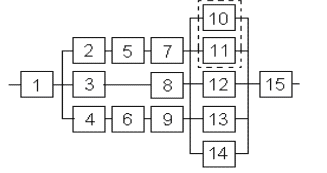 Рисунок 1- Исходная схема. Решение. 1.В исходной схеме элементы 2, 5, 7; 3, 8; 4, 6, 9 соединены последовательно, заменим их квазиэлементами А, В, Е соответственно, учитывая что элементы 2-9 - одинаковые: РА= РЕ =Р2Р5Р7= Р4Р6Р9 =Р23 РВ=Р3Р8=Р32 Где Pn Вероятность безотказной работы элемента n, Q вероятность отказа. 2.Элементы 10, 11, 12, 13, 14 образуют соединение “2 из 5”, которое заменяем элементом D. Суть системы заключается в том что она будет работоспособной если хотя бы 2 из 5 элемента работоспособны. Так как Р10=Р11=Р12=Р13=Р14, то для определения вероятности безотказной работы элемента D можно воспользоваться комбинаторным методом: 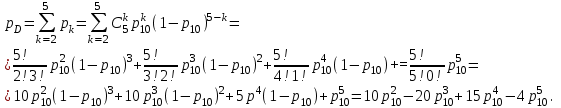 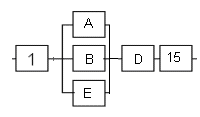 Рисунок 2- Преобразованная схема с квазиэлементами А, В, Е, D. 3. Элементы A, B, E образуют параллельное соединение, которое можно заменить элементом G: PG=[1-(1-PA)(1-PB)(1-PE)] Формула для системы с равно надёжными элементами 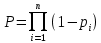 Рисунок 3 – Преобразованная схема 4. Элементы 1, G, D, 15 соединены последовательно, тогда вероятность безотказной работы всей системы будет определяться как: РС=Р1РGPDР15 5. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 1) подчиняются экспоненциальному закону: 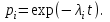 6. Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле (6) для наработки до 2,4 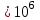 часов представлены в таблице 2. часов представлены в таблице 2.7. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, E, G, D, РС по формулам (1) - (5) также представлены в таблице 2. 8. На рисунке 4 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t. 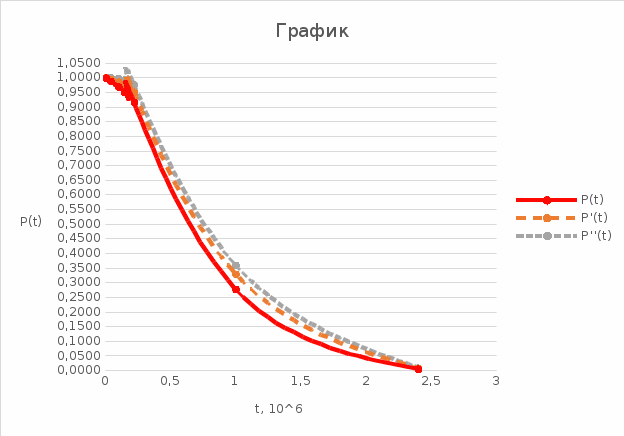 Рисунок 4. Изменение вероятности безотказной работы исходной системы Р(t), системы с повышенной надежностью элемента Р`(t) и системы со структурным резервированием элементов Р``(t). 9. По графику (рис.4, кривая P(t)) находим для  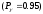 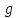 - процентную наработку системы - процентную наработку системы  ч. ч.Процентная наработка системы T Время наработки до отказа 10. Проверочный расчет при  ч показывает (таблица 2), что ч показывает (таблица 2), что  . . 11. По условиям задания повышенная  - процентная наработка системы - процентная наработка системы  ч. ч.12. Расчет показывает (таблица 2), что при  ч для элементов преобразованной схемы (рис. 3) ч для элементов преобразованной схемы (рис. 3)  , ,  , ,  , ,  . Следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент 1 и именно увеличение его надежности даст максимальное увеличение надежности системы в целом. . Следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент 1 и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.13. Для того чтобы при  ч система в целом имела вероятность безотказной работы ч система в целом имела вероятность безотказной работы  , необходимо, чтобы элемент 1 имел вероятность безотказной работы , необходимо, чтобы элемент 1 имел вероятность безотказной работы  14. Таким образом, интенсивность отказа элемента 1 должна быть:  ч-1 ч-1λ Интенсивность отказов элемента Мы снизили интенсивность отказа 1-го элемента с  до до  , то есть примерно в 7 раз. , то есть примерно в 7 раз.15. Результаты расчетов вероятности безотказной работы элемента 1 приведены в таблице 2. Там же приведены расчетные значения системы в целом P`(t). При  ч вероятность безотказной работы элемента 1 равна Р1=0,9934, системы - ч вероятность безотказной работы элемента 1 равна Р1=0,9934, системы -  , что соответствует условиям задания. График приведен на рисунке 4. , что соответствует условиям задания. График приведен на рисунке 4.16. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования – выбираем элемент 1 и 15. Для повышения надежности системы добавляем к 1 и 15 элементы, идентичные по надежности исходным элементам, до тех пор, пока вероятность безотказной работы системы не достигнет заданного значения. 17. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 1) достроить элементы 1 и 15 элементами 1а и 15а. (рис. 5). Результаты расчетов приведены в таблице 2.  Рисунок 5- Структурная схема системы после структурного резервирования. 18. Расчеты показывают, что при  ч ч  , что соответствует условию задания. , что соответствует условию задания.19. На рисунке 4 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элемента 1 (кривая  (t)) и после структурного резервирования (кривая (t)) и после структурного резервирования (кривая  (t)). (t)).Таблица 2 – Результаты расчетов вероятности безотказной работы системы
Выводы: 1. На рис. 4 представлена зависимость вероятности безотказной работы системы (кривая 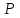 (t)). Из графика видно, что 95% - наработка исходной системы составляет (t)). Из графика видно, что 95% - наработка исходной системы составляет 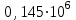 часов. часов.2. Для повышения надежности и увеличения 95% - наработки системы в 1.5 раза (до 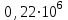 часов) использованы два способа: часов) использованы два способа:а) повышение надежности элемента 1 путем снижения интенсивности отказа до 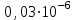 ч ч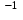 ; ;б) структурное резервирование элементов 1, 15 идентичными по надежности резервными элементами 1а, 15а (рис.5). 3. Анализируя зависимости вероятностей безотказной работы системы от времени (наработки) (рис. 4), можно сказать, что повышение надежности системы двумя способами практически одинаково, существует лишь небольшое отличие в пользу структурного резервирования, так как вероятность безотказной работы системы при структурном резервировании (кривая 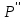 (t)) немного выше, чем при увеличении надежности элемента (кривая (t)) немного выше, чем при увеличении надежности элемента (кривая 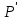 (t)). (t)). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
