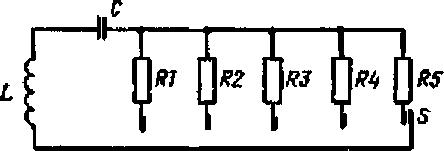Курсовая. Норматов. тюменский индустриальный университет многопрофильный колледж нефтегазовое отделение им. Ю. Г. Эрвье

• Название: тюменский индустриальный университет многопрофильный колледж нефтегазовое отделение им. Ю. Г. Эрвье
• Анкор: Курсовая
• Дата: 14.09.2022
• Размер: 1.86 Mb.
• Имя файла: Норматов.docx
• Тип: Курсовая; #676427
• страница: 1 из 7

М ИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ

«ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»

МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ

НЕФТЕГАЗОВОЕ ОТДЕЛЕНИЕ ИМ. Ю.Г. ЭРВЬЕ

МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ

Нефтегазовое отделение имени Ю.Г.Эрвье
21.02.10 Геология и разведка нефтяных и газовых месторождений
Аппаратура электромагнитного каротажного зондирования для исследования нефтяных скважин
КУРСОВАЯ РАБОТА


Выполнил: обучающийся

группы ГНГт-20-(11)-2

Норматов А.

Проверила: преподаватель

первой квалификационной

категории Блинова Ю.А.

Тюмень, 2022
СОДЕРЖАНИЕ

]К_ 34

4 = 4 L ^; IT

Г ^{= ia)}v^sA2 40

А," МЧ+kt) 40

Uc у 41

Я,=^Т-( 1-*V, 49

8p = (k^Tky^xk^T8g 60

ЗАКЛЮЧЕНИЕ ПО

ВВЕДЕНИЕ

Объектом исследования в работе являются методы достоверной оценки пространственного распределения удельного электрического со­противления (УЭС) в околоскважинной части терригенного разреза, включая разработку метрологического обеспечения аппаратуры, изуче­ние характеристик пространственного разрешения зондов электромаг­нитного каротажа и связанных с этим особенностей поведения диа­грамм в различных пластах.

Построение алгоритмов и эффективность быстрой автоматической инверсии напрямую связаны с правильным определением погрешностей измерения. Массовое применение аппаратуры высокочастотного каро­тажного изопараметрического зондирования (ВИКИЗ) при проведении ГИС на нефтегазовых месторождениях Западной Сибири привело к его включению в обязательный комплекс и использованию при подсчете запасов. В этой связи предъявляются повышенные требования к досто­верности результатов, которые являются основным, а в некоторых слу­чаях единственным источником информации для определения истинно­го распределения УЭС в околоскважинном пространстве, определения типа флюидонасыщения и коэффициентов нефтегазонасыщения. По­этому весьма актуальной является разработка метрологического обес­печения аппаратуры электромагнитного каротажа.

Цель исследований - развитие метода высокочастотного индукци­онного каротажного изопараметрического зондирования через разра­ботку метрологического обеспечения и системы экспресс-инверсии, обу­словивших повышение достоверности информации о количественных и качественных характеристиках пород, вскрытых скважиной.

Решаемые научные задачи.

■ разработка способа и устройства метрологической поверки аппара­туры электромагнитного каротажа;

■ на основании информации о погрешностях измерений построение

алгоритмов и компьютерной системы экспресс-оценки пространст­венного распределения УЭС в тонкослоистом терригенном разрезе.

Серийно выпускаемое устройство для метрологической поверки ИМ-1, представляющее собой набор из пяти колец, а также устройство для крепления и перемещения кольца на корпусе скважинного прибора сертифицировано Сибирским государственным институтом метрологии для проведения поверки аппаратуры. Все геофизические предприятия, где применяется метод ВИКИЗ, в настоящее время используют имита­тор ИМ-1 для периодической поверки приборов, согласно предложен­ной методике.

Используя предложенный способ и устройство, удалось доказать, что в основном диапазоне измерения разности фаз, от 4° до 50 °, отно­сительная погрешность для всех зондов ВИКИЗ не превышает 3 %.

Глава 1. Теоретические основы, применительно к задачам метрологии

1. 
   Современное состояние электрических методов ГИС
   

Одна из основных задач геофизических методов, связанных с оп­ределением коллекторских свойств и флюидонасыщения горных пород, состоит в обеспечении подсчета запасов нефти и газа [25]. Промыслово­геофизическую информацию широко используют при разведке, проек­тировании разработки нефтегазовых месторождений, а также для кон­троля и управления процессом эксплуатации.

К основным параметрам, определяемым по данным каротажа, можно отнести следующие: эффективная толщина коллектора, положе­ние водонефтяного (ВНЕ), газоводяного (ГВК), газонефтяного (ГНК) и текущих контактов на различных этапах разработки, коэффициенты пористости для большинства продуктивных объектов (за исключением отдельных типов сложных коллекторов), коэффициенты нефтегазона­сыщения, проницаемости и глинистости коллекторов.

Достоверность подсчета запасов нефти и газа в первую очередь зависит от правильной оценки эффективной мощности продуктивных коллекторов, локализации водонефтяного, газонефтяного и газоводяного контактов, границ литологического выклинивания продуктивных гори­зонтов.

При соответствующем качестве геофизических данных, достаточ­ной полноте используемого комплекса и знании петрофизических свя­зей между геофизическими и подсчетными параметрами геологического объекта, при правильной оценке типа коллектора и применении обосно­ванных способов интерпретации, возможно получение более представи­тельной, чем по анализу керна, информации об изучаемом коллекторе.

Основу ГИС в открытом стволе составляют электрические (БЕЗ, ЕС, ПС, БЕ) и электромагнитные методы (ИЕ, ВИЕИЗ и др.) [1, 2, 3, 4, 21].

Преимущества индукционного каротажа перед методом бокового каротажного зондирования общеизвестны. Это лучшие вертикальные характеристики, слабая зависимость от изолирующих прослоев, мень­шее влияние скважины. Это позволяет использовать кажущиеся значе­ния сопротивлений в широком диапазоне контрастов УЭС пластов и промывочной жидкости.

Индукционный каротаж [2, 18] положительно зарекомендовал себя в практике промысловой геофизики. В Западной Сибири геолого­технические условия (относительно низкие УЭС исследуемых пород, пресные промывочные жидкости) благоприятны для использования ин­дукционного каротажа. Тем не менее, и здесь существует ряд естест­венных ограничений.

В первую очередь - это повышенные удельные сопротивления от­дельных пластов. В этих случаях величина полезного сигнала очень сильно уменьшает значения, и диаграммы электропроводности стано­вятся мало отличимыми от нуля и из-за высоких погрешностей изме­рения не подлежат интерпретации. Другим ограничением является их недостаточно высокое пространственное разрешение, что снижает воз­можности детального исследования, как самого тонкослоистого разреза, так и зон проникновения.

Устранение большинства из указанных недостатков возможно с помощью высокочастотных методов электромагнитного каротажа, в ча­стности, высокочастотного индукционного каротажного изопараметри­ческого зондирования (ВИКИЗ), предложенного Ю. Н. Антоновым [2, 3].

Одним из способов выделения коллекторов по радиальному гради­енту сопротивления между глинистой коркой на стенке скважины и промытой частью пласта являются измерения микрозондами. Вместе с тем, достоверность этих измерений не всегда является достаточной. Это имеет место при образовании мощной глинистой корки, существенной неизометрии сечения скважины и др.

Из других электрических методов, предназначенных для выделе­ния пластов-коллекторов по радиальному градиенту УЭС, широко ис­пользуется боковое каротажное зондирование (БКЗ) с применением не­скольких однотипных зондов различной длины. БКЗ позволяет полу­чить кривые радиального зондирования, по которым устанавливается характер проникновения (повышающее или понижающее) фильтрата бурового раствора в пласт и в некоторых случаях его истинное УЭС.

Вместе с тем, методу БКЗ присущи значительные ограничения в определении радиального изменения УЭС [12, 7,19]. К ним можно отне­сти случаи исследования тонких коллекторов; мощных пластов с высо­коомными прослоями; терригенных толщ, представленных тонким пе­реслаиванием песчаников и глин различного сопротивления (эффект анизотропии); а также пластов-коллекторов со значительным проник­новением фильтрата, образовавшего протяженную и однородную про­мытую зону.

Обычно применяются двухзондовые методы определения радиаль­ного изменения сопротивлений с использованием двух существенно различных по длине зондов БКЗ или фокусированных зондов БК - ИК, МБК — БК и т.п. Комплексирование данных фокусирующих систем имеет ряд преимуществ по сравнению с зондами КС, которым свойст­венны ограничения БКЗ.

Кроме того, результаты измерений удельного сопротивления пород (или их электропроводности) различными методами электрокаротажа (БКЗ, БК, ИК и т.д.) могут отличаться даже в однородной среде не только из-за разнообразия источников возбуждения поля и особенно­стей пространственного распределения токов в среде, но и в силу тех­нических различий в градуировке измеряемых величин.

Основная задача электромагнитного каротажа заключается в вы­делении относительно однородных пластов и определении их удельного сопротивления (в том числе в зоне проникновения с оценкой её разме­ра).

К настоящему времени разработано и, в той или иной мере, ис­пользуется на практике значительное количество типов и модификаций скважинной аппаратуры для исследования электрических свойств гор­ных пород с самыми разнообразными зондами и техническими пара­метрами.

Традиционным и до сих пор наиболее широко применимым в тер- ригенном разрезе методом электрического каротажа является предло­женный в 1929 году Г. Долл ем метод потенциала самопроизвольной по­ляризации скважины (ПС). Для его измерения применяется установка с двумя электродами, один из которых находится в скважине, а другой — на земной поверхности. Изменение разности потенциалов при пере­мещении электрода измерительной установки вдоль ствола скважины и представляет собой диаграмму ПС.

Дальнейшее развитие индукционного каротажа привело к созда­нию таких его новых модификаций как индукционный каротаж с реги­страцией активной и реактивной составляющей сигнала, двухзондовый ИК, высокочастотный индукционный каротаж (ВИК) [4], индукционное каротажное зондирование (ИКЗ), высокочастотное индукционное каро­тажное изопараметрическое зондирование (ВИКИЗ), индукционный ка­ротаж поперечной проводимости (ИК-ПП). Большой вклад в развитие этих методов внесли В. С. Даев, Ю. Н. Антонов, К. Л. Санто, М. И. Эпов, Г. X. Шерман.

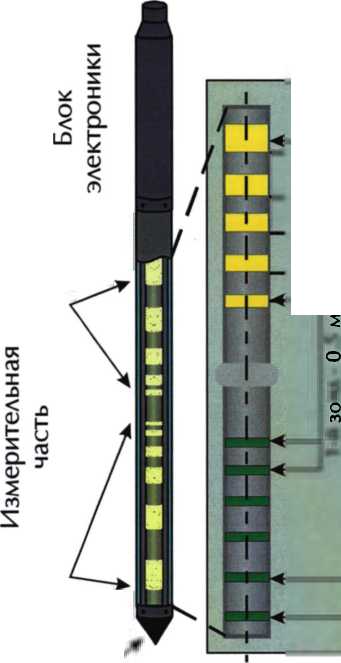
Аппаратура ВИКИЗ, разработанная в Институте геофизики СОАН СССР предназначена для определения УЭС горных пород в неф­тяных и газовых скважинах с помощью пяти зондов различной глубин­ности исследования, приняты наименования зондов в порядке возраста­ния длинны: DF05, DF07, DF10, DF14, DF20. Каждый зонд аппаратуры ВИКИЗ содержит одну генераторную и две измерительные катушки. Параметры зондов ВИКИЗ: отношение длины базы АЬк длине зонда L равно 0.2; коэффициент электродинамического подобия (произведение рабочей частоты зонда на квадрат его длины, /Д,) равен 3.5-10⁶ Гц-м²,

самый короткий зонд длиной 0.5 м работает на частоте 14 МГц, рабочая частота каждого следующего зонда вдвое меньше частоты предыдуще­го. Под длиной базы здесь понимается расстояние между центрами из­мерительных катушек, а под длиной зонда - расстояние между центра­ми генераторной и более удаленной от нее измерительной катушек. От­ношение базы к длине зонда остается постоянной.

Измеряемой характеристикой является разность фаз Дф между э.д.с., наведенными в измерительных катушках каждого зонда. При вы­полнении этих условий показания всех зондов в однородной среде бу­дут одинаковыми. Величина Дф непосредственно связана с УЭС горных пород в околоскважинном пространстве. Диапазон измерения Дф - от 1 до 67°, что соответствует диапазону изменения УЭС от 200 до 0.4 Ом-м.

0
Измерительные катушки

Электрод ПС
.875 МГи

_
Генераторные
катушки
3.5 МГи _ 7.0_МГц

5 О CN

* (

О

Современная аппаратура индукционного каротажа поверяется пре­имущественно с помощью имитаторов р, выполненных в виде индукци­онной катушки, в цепь которой последовательно включаются резисторы и емкость для компенсации реактивной составляющей комплексного со­противления.

На рисунке приведена принципиальная схема имитатора для аппа­ратуры ИК, входящего в состав установки УПЭК-1.







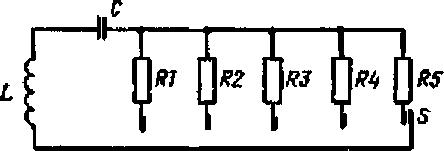
Индукционная катушка L выполнена на гетинаксовом каркасе и содержит 10 витков множительного медного провода (для повышения добротности и уменьшения скин-эффекта) со средним диаметром на­мотки 360 мм. В составе установки УПЭК имеется вторая катушка с диаметром намотки 700 мм. Емкость конденсатора С подбирается экс­периментально таким образом, чтобы на частотах 25 и 50 кГц индук­тивное сопротивление цепи равнялось емкостному сопротивлению. Со­противления резисторов Rl - R5 (магазины сопротивлений) определяют для каждого типа зонда аппаратуры ИК путем математического модели­рования электромагнитного поля в имитаторе и в бесконечной однород­ной среде. Резисторы Rl - R5 переключают при помощи переключателя. В аппаратуре АИК-5 имитации значений реактивной составляющей удельного электрического сопротивления (проводимости) производится из­менением емкости конденсатора С.

Поверку аппаратуры ИК выполняют в следующей последователь­ности [13]:

1. 
   зонд аппаратуры ИК располагают горизонтально на диэлектри­ческих подставках высотой не менее 1.5 м и размещают на нем вблизи генераторной катушки индукционную катушку имитатора;
   
2. 
   включают аппаратуру и по истечении времени ее самопрогрева выполняют калибровку по стандарт-сигналам в соответствии с техниче­ским описанием и инструкцией по эксплуатации;
   
3. 
   устанавливают на зонд вблизи генераторной катушки индукцион­ную катушку имитатора и, перемещая ее вдоль оси зонда, добиваются максимального сигнала на выходе поверяемой аппаратуры ИК;
   
4. 
   включают в цепь имитатора резистор (или магазин сопротивле­ний), значение сопротивления которого R_a соответствует началу диапа­зона измерений поверяемой аппаратуры и фиксируют результат изме­рений;
   
5. 
   измеряют поверяемой аппаратурой остальные значения, воспро­изводимые имитатором (в случае существенной случайной составляю­щей погрешности выполняют многократные измерения каждого значения);
   
6. 
   для каждого измеренного результата определяют оценку по­грешности аппаратуры.
   

1.2 Физико-математические основы метрологической поверки

Электрические свойства растворов электролитов

Электропроводность

С
■-Е


10"


(1.1)


ы щ

огласно [22], электропроводность системы, состоящей из п заря­женных частиц, находящихся в хаотическом движении и между кото­рыми отсутствует взаимодействие (аналогично частицам идеального га­за), может быть описана выражением

где v₍ - число частиц i -го вида в одном кубическом метре, q_h т,- — заряд и масса г -й частицы, ц - время релаксации.

В общем случае величину г„ характеризующую интервал времени между двумя столкновениями частицы, определить сложно. Однако р можно выразить через длину свободного пробега / и скорость движения

Т

Vo частицы. Поэтому величина —, называемая подвижностью р [47],

m

м
т

м=—


1


m V₀m

Из кинетической теории газов [47] известно, что

-mV} =-кТ 2 ⁰ 2


тогда р


]К_

ЗкТ'


(1.2)

(1.3)

(1.4)

ожет быть описана следующим выражением:

здесь Т абсолютная температура, к — постоянная Больцмана.

IV

Произведение равно коэффициенту диффузии D движущихся

частиц. В то же время коэффициент диффузии равен [47]

/
(1.5)


D = -± 3
К кТ

6 кщ

где г_г - радиус движущихся частиц (м), г] - коэффициент динамиче­ской вязкости.

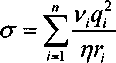Подстановка соотношений (1.4) и (1.5) в (1.1) дает для удельной электропроводности следующее выражение:

Соотношение (1.6) представляет известную формулу для удельной электропроводности электролитов. Оно справедливо лишь для очень слабых электролитов и обычно используется для определения эффек­тивных (стоксовских) радиусов частиц [52]. В этой области кулоновским взаимодействием можно пренебречь и движение частиц будет хаотич­ным, а их скорость будет определяться только температурой.

Увеличение содержания ионов в растворе приводит к увеличению влияния дальнодействующих сил кулоновского взаимодействия между частицами. Системы, состоящие из значительного числа заряженных частиц, характеризуются тем, что каждый отдельный ион находится в поле остальных ионов, но система в целом остается электронейтраль­ной. Последнее приводит к тому, что в растворе для системы ионов ус­танавливается определенная регулярная структура. В то же время те­пловое движение частиц стремится нарушить эту структуру. Это при­водит к непрерывной флюктуации полей как по величине, так и по на­правлению. В реальных системах, на движения ионов влияют не только температура, но и поля, создаваемого зарядами. Вследствие этого и значения времени релаксации г_; будет изменяться.

Следовательно, тепловая энергия будет расходоваться не только на движение частиц, но и на преодоление энергии кулоновского поля U_k

(1.7)

Из (1.2) - (1.6), с учетом (1.7) получается для удельной электропро­водности следующее выражение:

f
(1.8)

кя-ит

^₂ блщ(ЗкТ-2U_k)

В основе этого способа расчета удельной электропроводности силь­ных электролитов лежит предположение, о том, что ионы не движутся, а лишь хаотически колеблются около своих положений равновесия. Т. е. в растворах существует не только определенная структура растворите­ля [40], но и структура растворенного вещества. В концентрированных растворах последняя может быть подобна кристаллической структуре. Таким образом, при расчете энергии кулоновского взаимодействия можно использовать метод расчета энергии кристаллической решетки по Борну [39]

Ы
(1.9)


и_к=-
г^А

Алеева ^ s )

где <7, - заряды ионов, s - относительная диэлектрическая прони­

ц
трами ионов, А - структурная постоянная,


'i-Г


V


SJ


множитель, учиты­

аемость, £q - диэлектрическая постоянная, а - расстояние между цен­

вающий энергию отталкивания.

В слабоконцентрированных растворах расстояния между ионами значительно больше, чем в кристаллах, и поэтому силы отталкивания можно не учитывать. Однако при концентрациях электролитов больше 1 Моль/литр эти расстояния становятся одного порядка и необходимо учитывать силы отталкивания.

Расчет удельной электропроводности растворов NaCl по формулам (1.8) - (1.9) показал их хорошее совпадение со справочными данными [10, 44]. Поэтому они в дальнейшем используются для расчетов УЭС растворов электролитов с учетом температуры и концентрации.

Практически важной является оценка частотной дисперсии элек­тропроводности растворов электролитов. Из работ [26, 45, 49] следует, что она обусловлена в первую очередь дисперсией дипольной электро­проводности воды и составляет пренебрежимо малую величину (поряд­ка ЗЮ^-7 См/см) при рассматриваемых нами частотах (порядка 10⁶­10⁷ Гц) и концентрациях (1 Моль/литр). Поэтому, при дальнейшем рас­смотрении этим эффектом можно пренебречь.

Диэлектрическая проницаемость

Анализ литературы [45, 49] показал, что в настоящее время нет общей точки зрения на величину диэлектрической проницаемости рас­твора той или иной соли. По мнению одних авторов диэлектрическая проницаемость бинарного раствора электролита увеличивается с ростом концентрации, по мнению других - уменьшается, или, в зависимости от состава солей, возрастает или уменьшается. Тем не менее, в большин­стве случаев эти изменения малы и в первом приближении могут быть рассчитаны по формуле (1.10) Г. Фалькенгагена [46]. При этом предпо­лагается, что с ростом концентрации солей диэлектрическая проницае­мость растворов должна увеличиваться.

£*=^+3.7971 (1.10)

где е - диэлектрическая проницаемость раствора;

£*₀- диэлектрическая проницаемость дистиллированной воды;

Л - концентрация раствора, Моль/литр.

Большинство исследователей сходится на том, что с увеличением температуры раствора его диэлектрическая проницаемость уменьшает­ся. Это подтверждается и экспериментальными данными для водного раствора NaCl [10].

т° с	Концентрация, Моль/литр
	0.125	0.333	0.66	1.00	2.08	4.34	5.62
3	85.8	81.9	77.2	74.0	-	-	-
25	78.0	73.0	68.7	65.0	52.2	37.6	32.1
40	71.5	69.7	67.1	64.3	-	-	-

Таким образом, можно сделать следующие выводы: с увеличением минерализации диэлектрическая проницаемость би­нарных растворов в сравнении с диэлектрической проницаемостью дистиллированной воды изменяется незначительно; с увеличением температуры диэлектрическая проницаемость бинар­ных растворов существенно уменьшается.

Следовательно, в случае применения в метрологических моделях, диэлектрические свойства растворов можно считать независящими от концентрации соли, а учет температурных зависимостей необходим на­ряду с учетом температуры для электропроводности. Для этого необхо­димо проводить тщательные измерения температуры до и после прове­дения работ.

1.3 Электромагнитное поле магнитного диполя

Уравнения Максвелла для квазистационарного поля:

rotЁ = -—\ div7 = 0
dt

rotН = aj ; divB = 0

где о - удельная электропроводность среды.

Уравнения связи j = аЁ, В = pH.

Будем предполагать, что размеры генераторной катушки сущест­венно меньше расстояния до точки измерения. В этом случае круглый виток с переменным током I(t) = 1₀е^ш, можно заменить на диполь с из­меняющимся во времени моментом: М = М₀е^ш, (О - циклическая часто­та.

В однородной среде

Введем цилиндрическую систему координат \r, <р, z). Ось z направ­лена вдоль момента диполя. Начало координат расположено в источни­ке. Введем вектор-потенциал А, связанный с электромагнитным полем следующими соотношениями:

Е = ico/u rot А Н = k² А + grad div А

где: к¹ - -тар

В силу симметрии задачи существует всего три ненулевые компо­ненты поля

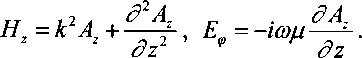Компонента потенциала подчиняется уравнению Гельмгольца

V²A_z + k²A_z = О, при R*0

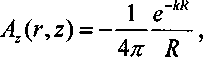Как известно, решение этого уравнения имеет вид

где R = ylr² +z² ,

тогда из (1.1) следует, что

E
4 nR
_r=i_m-^e“\\ + kR)

H_z=-^-_Te-^kR(l-kR) ^z In R^{3 V} '

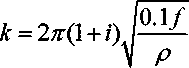При условии квазистационарности волновое число к преобразуется к виду

здесь f=co/2n частота в МГц.

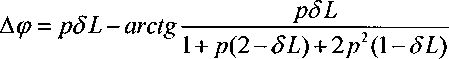При этом разность фаз между э.д.с в приемных катушках

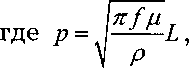5L- —, L - длина наибольшего зонда

В присутствии тонкой проводящей пластины

В случае, когда электропроводность слоя во много раз превышает электропроводность окружающей среды, а толщина слоя во много раз меньше длины зонда, то можно пренебречь распространением поля внутри слоя можно говорить о продольной проводимости слоя s = a-h, где а со - электропроводность слоя, h -» 0 - толщина слоя.

Граничные условия для вертикальной компоненты А_г следуют из непрерывности тангенциальных компонент поля

4 = 4 L ^; IT Г ^{= ia)}v^sA2

¹ dz dz

Т
Д =


\_ 4 л


V


/I


-i|,|


Ак²е^2Щ


А," МЧ+kt)


е²^ \J₀(Ar)dA;

огда для вектор-потенциала имеем:

2
e^J^Ar)dA


Д
А

4л *2A_l+k_s где k² = -icojus.

Д
_Я1 _=Ho₊!®i^usz Г ^те


3 -т(1+2^)


00 3 -ГП\

m е ¹


2т_х - ico/usz


2 ' т_х (2т_[ kopsz)

dm,


dm;

ля вертикальной компоненты магнитного поля на оси диполя, со­гласно (1.2):

где т- Az, m_l= sjm² -k²z² .

В цилиндрически-слоистой среде

При переходе через поверхность раздела г = а₁ тангенциальные

компоненты электрического и магнитного поля меняются непрерывно.

Для этого необходимо

д
^z² '


к² А\ + = к₂А₂ + -


dz


Тогда решение на оси среды имеет вид