тория вероятности ипз 8 вариант. ипз вариант 8. У пети есть 7 книг, а у Егора 9 книг. Сколькими способами они могут обменять три книги одного на три книги другого

• Название: У пети есть 7 книг, а у Егора 9 книг. Сколькими способами они могут обменять три книги одного на три книги другого
• Анкор: тория вероятности ипз 8 вариант
• Дата: 25.05.2022
• Размер: 3.63 Mb.
• Имя файла: ипз вариант 8.docx
• Тип: Документы; #549693

Вариант 8

1. 
   У Пети есть 7 книг, а у Егора – 9 книг. Сколькими способами они могут обменять три книги одного на три книги другого?
   

2. 
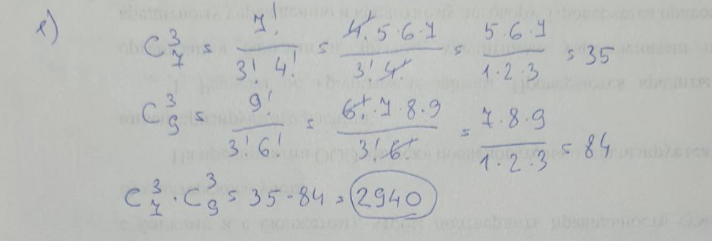   Из колоды в 52 листа вынимается одна карта наугад. Какова вероятность того, что это будет туз или дама?
   

3. 
   В вазе находится 10 конфет «Белочка», 6 конфет «Вдохновение», 4 конфеты «Шальная пчелка». Ребенок наугад берет 6 конфет. Какова вероятность, что среди них будет 4 конфеты «Белочка» и 2 конфеты
   

«Шальная пчелка»?

4. 
   Какова вероятность того, что три случайно встреченных на улице человека родились в понедельник?
   

5. 
   Фирма получает товар через трех посредников. Вероятности того, что посредник будет выполнять условия договора поставки в течение времени T, соответственно равны 0,8; 0,9; 0,9. Посредники могут
   

нарушить договор независимо друг от друга. По истечении времени T выяснилось, что товар на фирму не поступил. Найти вероятность того, что договор нарушил только третий посредник.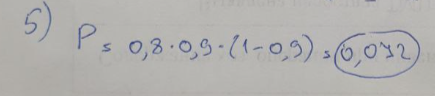

6. 
   Вероятность продажи акций с прибылью через год после покупки равна 0,8. независимо было продано 5 акций. Найти вероятность того, что прибыль будет получена ровно с двух из них.
   

7. 
   Баскетболист бросает мяч в корзину. Вероятность попадания мяча при каждом броске равна 0,7. Найдите вероятность того, что из 100 бросков баскетболист попадет ровно 75 раз.
   
   
8. 
   :
   

𝜉	-14	-13	-11	11	13
𝑃	0,2	𝑝	0,25	0,15	0,25

Найти:

а) неизвестную вероятность 𝑝;

б) функцию распределения𝐹(𝑥) и построить её график;

в) математическое ожидание𝑀[𝜉];

г) дисперсию𝐷[𝜉];

д) 𝑃 ⁽−14 <𝜉 ≤ 11) .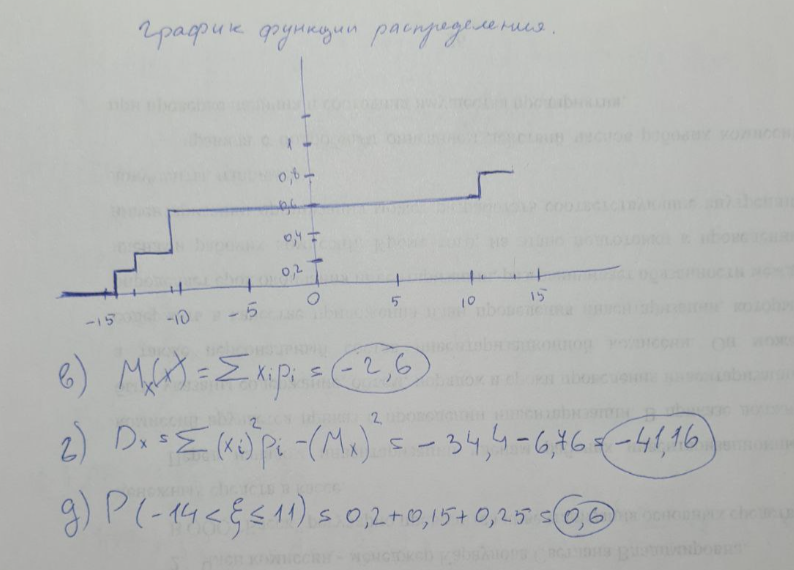

9. 
   Студент знает 6 из 10 вопросов зачета. В билете три вопроса. Случайная величина 𝜉 – количество вопросов из билета, которые студент знает. Построить вероятностный ряд для𝜉. Найти ее 𝑀[𝜉] и
   

𝐷[𝜉].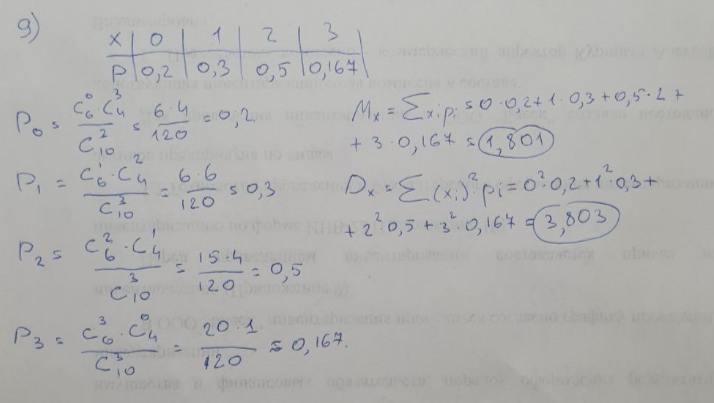

10. 
    Непрерывная случайная величина 𝜉 задана с помощью функции плотности распределения вероятностей𝑓(𝑥):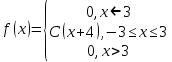
    

Найти: а) параметр 𝐶;

б) функцию распределения𝐹(𝑥) и построить ее график;

в) математическое ожидание𝑀[𝜉]и дисперсию 𝐷[𝜉];

г) 𝑃 ⁽−3 <𝜉 ≤ 10).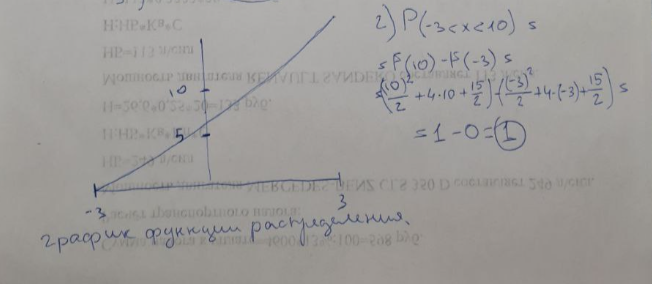

11. 
    Случайная величина 𝜉 распределена равномерно на [−1; 9]. Написать𝑓(𝑥)и 𝐹(𝑥). Найти 𝑀[𝜉] и 𝐷[𝜉]. Вычислить 𝑃 (−4 ≤ 𝜉 ≤ 7).
    

12. 
    Случайная величина 𝜉 распределена нормально с математическим ожиданием 𝑀[𝜉] = 1 и дисперсией 𝐷 𝜉 = 9. Написать ее функцию плотности распределения вероятностей𝑓 𝑥 и вычислить 𝑃(−5 ≤ 𝜉 ≤ 7).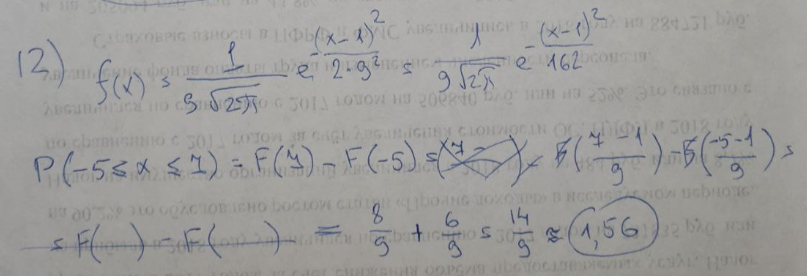