Учебная практика_215_21А. Учебная практика по курсу информатика

• Название: Учебная практика по курсу информатика
• Анкор: Учебная практика_215_21А.doc
• Дата: 21.02.2018
• Размер: 17.89 Mb.
• Имя файла: Учебная практика_215_21А.doc
• Тип: Методические указания; #15755
• страница: 16 из 17

Методические указания по решению транспортной задачи

В общем виде транспортную задачу можно сформулировать следующим образом: в m пунктах отправления A₁, …, A_m находится однородный груз, количество которого равно соответственно a₁, …, a_m единиц. Данный груз необходимо доставить потребителям B₁, …B_n, спрос которых – b₁, …b_n. Стоимость перевозки единицы груза из i-го () пункта отправления в j-й () пункт назначения равен с_ij. Необходимо составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимальны.

Математически транспортную задачу можно записать так: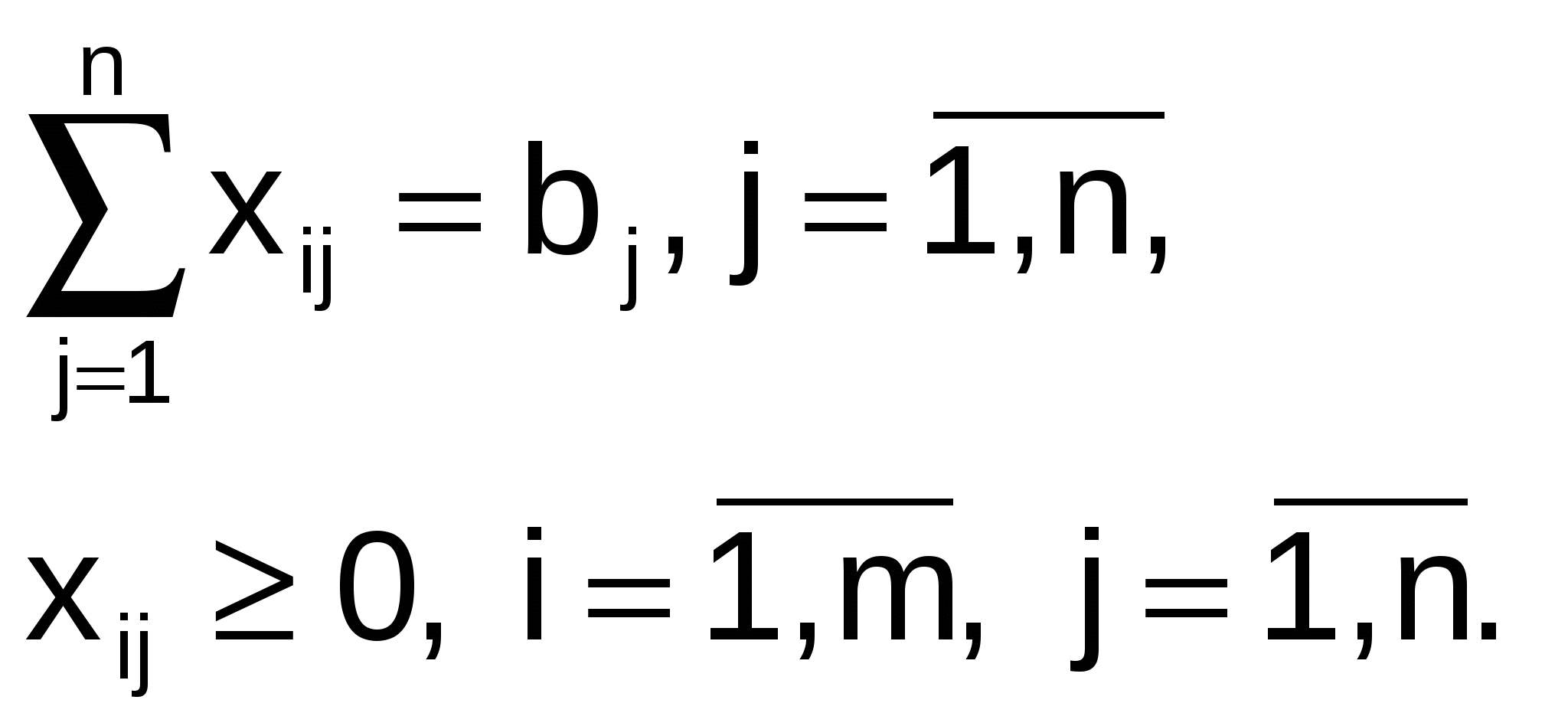
(5.1.)

(5.2)

(5.3)
Таким образом, даны система ограничений (5.2) при условии (5.3) и линейная функция (5.1). Требуется среди множества решений системы (5.2) найти такое неотрицательное решение, которое доставляет минимум линейной функции (5.1).

Модель транспортной задачи называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщика равен спросу потребителей, т.е. выполняется равенство:



Если для транспортной задачи выполняется одно из условий: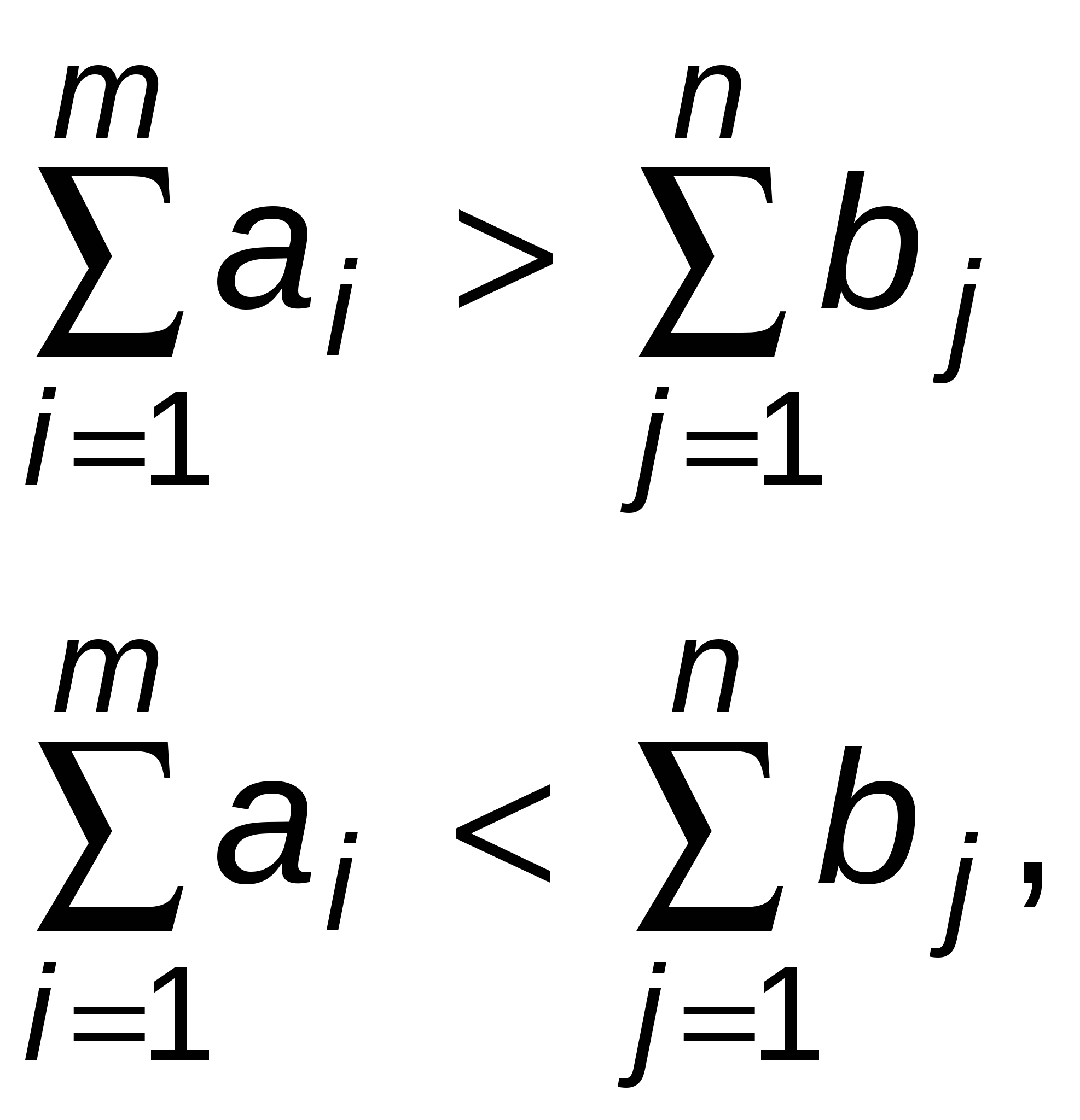



то модель задачи называют открытой (несбалансированной).

Для разрешимости транспортную задачу с открытой моделью следует преобразовать в закрытую.

Если выполняется условие , то необходимо ввести фиктивный (n+1) –й пункт назначения B_n+1, т.е. в матрицу задачи вводится дополнительный столбец. Спрос фиктивного потребителя принимается равным . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость складирования продукции), т.е. .

Если выполняется условие , то необходимо ввести фиктивного (m+1)-го поставщика A_m+1, т.е. в матрицу задачи вводится дополнительная строка. Запас груза данного поставщика принимается равным . Стоимость перевозок продукции полагается одинаковой, чаще всего равной нулю (если не задана стоимость штрафов за недопоставку продукции), т.е. .

При преобразовании открытой задачи в закрытую целевая функция не меняется, т.к. все слагаемые, соответствующие дополнительным перевозкам, равны нулю.

FПример.Производство продукции осуществляется на 4-х предприятиях, а затем развозится в 5 пунктов потребления. Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Хранение на предприятии единицы продукции обходится в 2 у.е. в день, штраф за недопоставленную продукцию – 3,5 у.е. в день. Стоимость перевозки единицы продукции (в у.е.) с предприятий в пункты потребления приведена в таблице 5.1.

Таблица 5.1

Стоимость перевозки единицы продукции

Предприятия	Пункты потребления
	1	2	3	4	5
1	3,2	3	2,35	4	3,65
2	3	2,85	2,5	3,9	3,55
3	3,75	2,5	2,4	3,5	3,4
4	4	2	2,1	4,1	3,4

Решение

1. 
   Проверка сбалансированности модели задачи – модель является сбалансированной, т.к. суммарный объем производимой продукции в день равен суммарному объему потребности в ней:
   

235+175+185+175=125+160+60+250+175.

Поэтому при решении этой задачи не учитываются издержки, связанные со складированием и недопоставкой продукции.

2. 
   Построение математической модели – неизвестными в этой задаче являются объемы перевозок. Пусть x_ij – объем перевозок с i–го предприятия в j–й пункт потребления. Суммарные транспортные расходы – это функционал качества (критерий цели):
   

где c_ij – стоимость перевозки единицы продукции с i-го предприятия в j-й пункт потребления.

Неизвестные в этой задаче должны удовлетворять следующим ограничениям:

• 
  объемы перевозок не могут быть отрицательными.
  
• 
  поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятий, а потребности всех пунктов потребления должны быть полностью удовлетворены.
  

Итак, имеем следующую задачу:

• 
  найти минимум функционала:
  

• 
  при ограничениях:
  

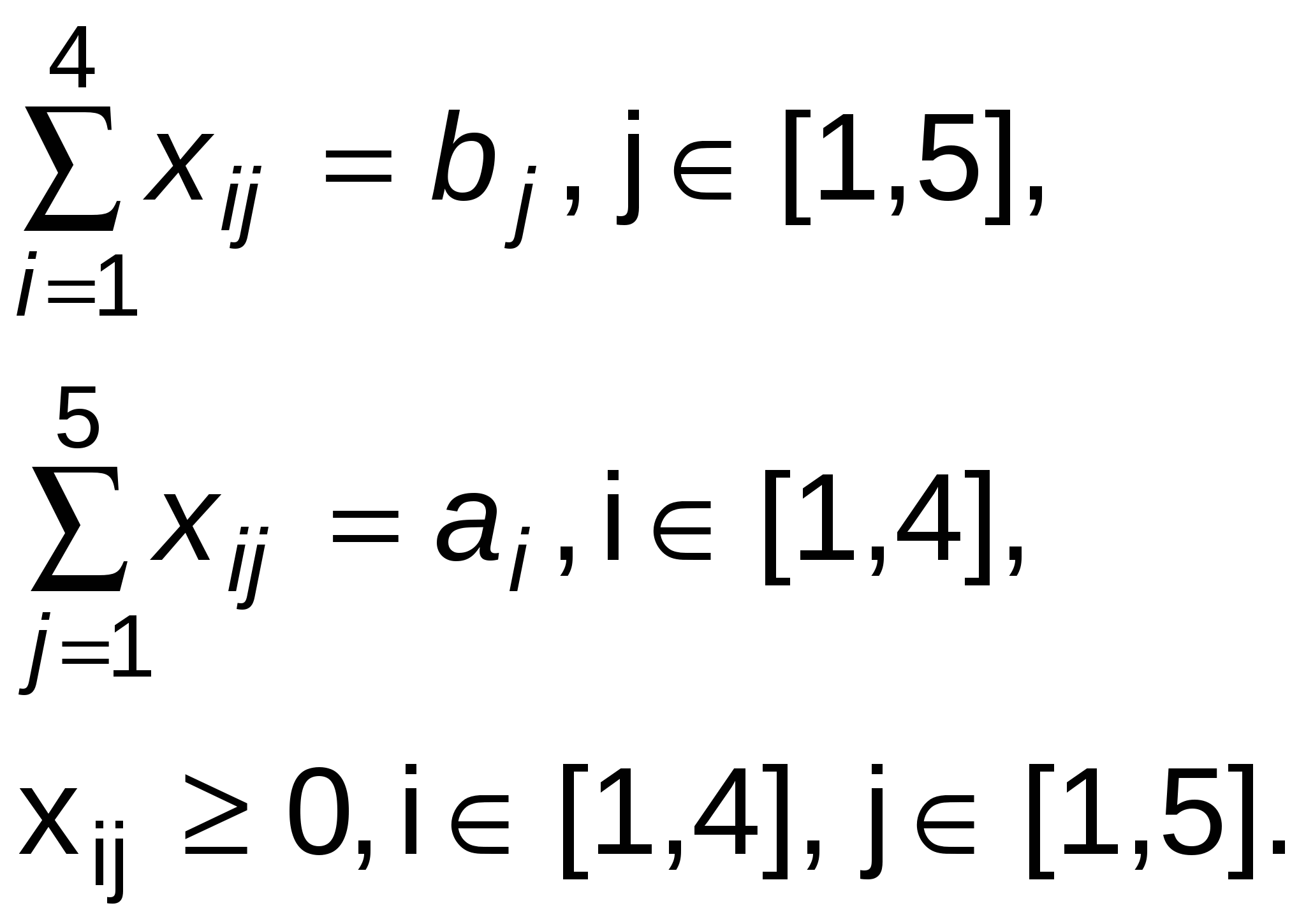где a_i – объем производства на i–м предприятии, b_j - спрос в j–м пункте потребления.

3. 
   Решение задачи с помощью окна Поиск решения:
   

Подготовку рабочего листа для задачи осуществляем в соответствии с рис. 5.1., формулы для расчета приведены в таблице 5.2.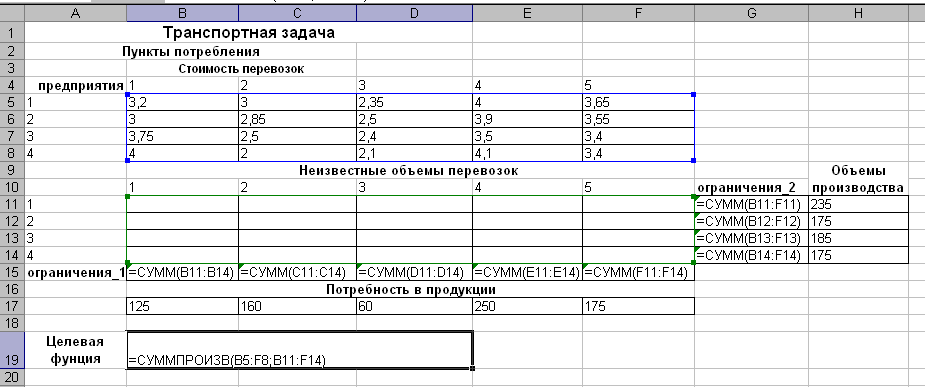



Рис. 5.1. Исходные данные для решения транспортной задачи

Таблица 5.2

Формулы расчетов

Описание	Ячейка	Формула
Ограничения_1	G11	=СУММ(B11:F11)
	G12	=СУММ(B12:F12)
	G13	=СУММ(B13:F13)
	G14	=СУММ(B14:F14)
Ограничения_2	B15	=СУММ(B11:B14)
	C15	=СУММ(C11:C14)
	D15	=СУММ(D11:D14)
	E15	=СУММ(E11:E14)
	F15	=СУММ(F11:F14)
	B19	=СУММПРОИЗВ(B5:F8.B11:F14)

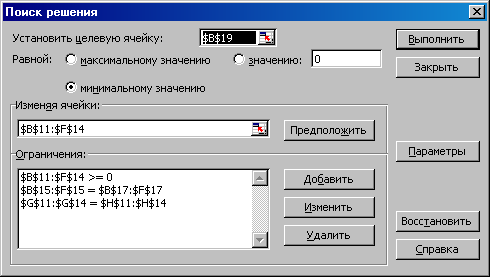Рис. 5.2. Ввод данных в окно Поиск решения для транспортной задачи

Ввод данных в окно Поиск решения производим в соответствии с рис. 5.2.. полученное оптимальное решение представлено на рис. 5.3.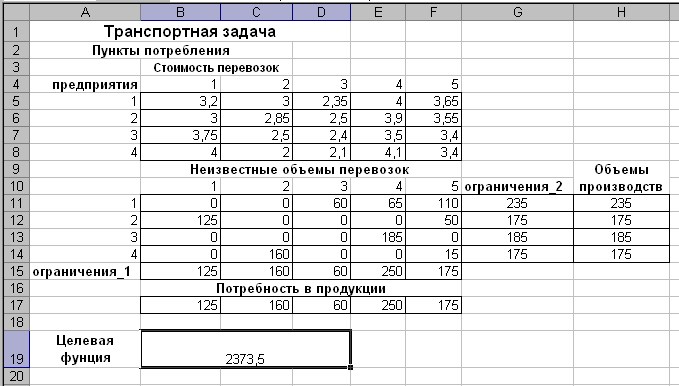


Рис. 5.3. Оптимальное решение для транспортной задачи
Лабораторная работа №6.

Использование макросов в MS EXCEL

ЗАДАНИЕ

1. Создайте макрос в вашей рабочей книге на языке Visual Basic.

2. Назначьте макросу комбинацию клавиш для быстрого вызова.

3. Назначьте макросу пункт меню Сервис.

4. Проверьте работоспособность макроса.