Концепции современного естествознания_под ред Михайлова Л.А_Учебник_2008 -336с. Концепции современного естествознания_под ред Михайлова Л.А_Учеб. Учебник для вузов Издательство Питер, 2008 г. 336 стр

• Название: Учебник для вузов Издательство Питер, 2008 г. 336 стр
• Анкор: Концепции современного естествознания_под ред Михайлова Л.А_Учебник_2008 -336с.doc
• Дата: 28.05.2017
• Размер: 2.28 Mb.
• Имя файла: Концепции современного естествознания_под ред Михайлова Л.А_Учеб.doc
• Тип: Учебник; #8195
• страница: 4 из 23

Глава 3 ПРОСТРАНСТВО, ВРЕМЯ, ПРИНЦИПЫ ОТНОСИТЕЛЬНОСТИ
3.1. Ньютоновская концепция абсолютного пространства и времени. Законы движения

Вопросы пространства и времени всегда интересовали человеческое общество. Одна из концепций этих понятий идет от древних атомистов – Демокрита, Эпикура и др. Они ввели в научный оборот понятие пустого пространства и рассматривали его как однородное и бесконечное.

В процессе создания общей картины мироздания Исаак Ньютон (1642–1726), конечно, также не мог обойти вопрос понятия пространства и времени.

В 1687 г. он опубликовал труд «Математические начала натуральной философии», который стал вершиной достижений естествознания XVII в.

По Ньютону, мир состоит из материи, пространства и времени. Эти три категории независимы друг от друга. Материя размещается в бесконечном пространстве. Движение материи происходит в пространстве и времени. Ньютон разделял пространство на абсолютное и относительное. Абсолютное пространство неподвижно, бесконечно. Относительное – это часть абсолютного. Так же он классифицировал и время. Подабсолютным, истинным (математическим) временем он понимал время, которое течет всегда и везде равномерно, а относительное время, по Ньютону, есть мера продолжительности, которая существует в реальной жизни: секунда, минута, час, сутки, месяц, год. У Ньютона абсолютное время существует и длится равномерно само по себе, безотносительно к каким-либо событиям. Абсолютное пространство и абсолютное время представляют собой вместилище всех материальных тел и пространств и не зависят ни от этих тел, ни от этих процессов, ни друг от друга.

Массу Ньютон определяет как количество материи и вводит понятие «пассивной силы» (силы инерции) и «активной силы», создающей движение тел.

Изучив и выявив закономерности движения, Ньютон таким образом сформулировал его законы:

1– й закон. Всякому телу продолжать свое состояние покоя или равномерного прямолинейного движения, поскольку оно не принуждается приложенными силами изменять это состояние.

2– й закон. Изменению движения быть пропорциональным приложенной движущей силе и происходить по направлению той прямой, по которой эта сила действует.

3– й закон. Действию всегда встречать равное противодействие, или воздействию двух тел друг на друга быть между собой равными и направленными в противоположные стороны.

В наше время знаменитые законы формулируются в более удобной форме:

► 1. Всякое материальное тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Стремление тела сохранить состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон называют также законом инерции.

► 2. Ускорение, приобретаемое телом, прямо пропорционально силе, действующей натело, и обратно пропорционально массе тела.

► 3. Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.

Второй закон Ньютона нам известен в виде

F = m × a, или a = F/m,

где ускорение а, получаемое телом поддействием силы F, обратно пропорционально массе тела m. Величина m называется инертной массой тела, она характеризует способность тела оказывать сопротивление действующей («активной») силе, то есть сохранять состояние покоя. Второй закон Ньютона справедлив только в инерциальных системах отсчета.

Первый закон можно получить из второго, так как в случае отсутствия воздействия на тело со стороны других сил ускорение также равно нулю. Однако первый закон рассматривается как самостоятельный закон, поскольку он утверждает существование инерциальных систем отсчета.

► Инерииальные системы отсчета – это такие системы, в которых справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы, взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.

Теоретически может существовать сколь угодно равноправных инерциальных систем отсчета, и во всех таких системах законы физики одинаковы. Это утверждает принцип относительности Галилея (1636 г.).

Научное доказательство существования всемирного тяготения и математическое выражение описывающего его закона стало возможным только на основе открытых И. Ньютоном законов механики. Закон всемирного тяготения был сформулирован Ньютоном в труде «Математические начала натуральной философии» (1687 г.).

Закон всемирного тяготения Ньютон формулирует в следующих тезисах: «тяготение существует для всех тел вообще и пропорционально массе каждого из них», «тяготение к отдельным равным частицам тел обратно пропорционально квадратам расстояний мест к частицам». Этот закон известен в виде:



где m₁, ш₂ – массы двух частиц, r – расстояние между ними, G – гравитационная постоянная (в системе СИ G = 6,672 · 10^-11 м²/кг²). Физический смысл гравитационной постоянной заключается в том, что она характеризует силу притяжения двух масс весом в 1 кг на расстоянии в 1 м.

Открыв закон всемирного тяготения, Ньютон смог дать ответ на вопрос, почему Луна обращается вокруг Земли и почему планеты движутся вокруг Солнца. В каждом отдельном случае он мог рассчитать силу тяготения. Но как передается взаимодействие между массами, притягивающимися друг к другу, какова природа этой силы, Ньютон объяснить не мог.

В трудах Ньютона тяготение – это сила, которая действует на больших расстояниях и как бы без какого-то материального посредника.

Это привело к понятию «дальнодействие». Природу «дальнодействия» Ньютон объяснить не мог. Он думал о каком-то материальном «агенте», с помощью которого осуществляется гравитационное взаимодействие, но в решении этой проблемы он потерпел неудачу. Основываясь на законе всемирного тяготения Ньютона, небесная механика допускает принципиальную возможность мгновенной передачи сигналов, что противоречит современной физике (общей теории относительности). Поэтому буквальное понимание закона тяготения Ньютона с современной точки зрения недопустимо.

Ньютоновская механистическая парадигма в естествознании господствовала более 200 лет, хотя и подвергалась критике по ряду позиций, в том числе и в понимании пространства и времени (Лейбниц, Гегель, Беркли и др.). В конце XIX и в начале XX в. возникли принципиально новые научные представления об окружающей природе. Появились новые парадигмы: сначала релятивистская, а затем квантовая (см. ранее). В физическую картину мира полноправно вошла концепция поля как материальной среды, связывающей частицы вещества, все физические объекты материального мира. В современной физике известны четыре вида взаимодействия материальных объектов: электромагнитное, гравитационное, сильное и слабое (см. выше). Они ответственны за все процессы взаимодействия.

3.2. Законы сохранения

Рассмотрим наиболее общие законы сохранения, которым подчиняется весь материальный мир и которые вводят в физику ряд фундаментальных понятий: энергия, количество движения (импульс), момент импульса, заряд.

Закон сохранения импульса

Как известно, количеством движения, или импульсом, называют произведение скорости на массу движущегося тела: p = mv Эта физическая величина позволяет найти изменение движения тела за какой-нибудь определенный промежуток времени. Для решения этой задачи следовало бы применять второй закон Ньютона бесчисленное число раз, во все промежуточные моменты времени. Закон сохранения количества движения (импульса) можно получить, используя второй и третий законы Ньютона. Если рассматривать две (или более) материальные точки (тела), взаимодействующие между собой и образующие систему, изолированную от действия внешних сил, то за время движения импульсы каждой точки (тела) могут изменяться, но общий импульс системы должен оставаться неизменным:

m₁v + m₁v₂ = const.

Взаимодействующие тела обмениваются импульсами при сохранении общего импульса.

В общем случае получаем: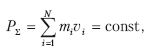



где P_Σ – общий, суммарный импульс системы, m_iv_i – импульсы отдельных взаимодействующих частей системы. Сформулируем закон сохранения импульса:

► Если сумма внешних сил равна нулю, импульс системы тел остается постоянным при любых происходящих в ней процессах.

Пример действия закона сохранения импульса можно рассмотреть на процессе взаимодействия лодки с человеком, которая уткнулась носом в берег, а человек в лодке быстро идет из кормы в нос со скоростью v₁. В этом случае лодка отойдет от берега со скоростью v₂:




Аналогичный пример можно привести со снарядом, который разорвался в воздухе на несколько частей. Векторная сумма импульсов всех осколков равна импульсу снаряда до разрыва.

Закон сохранения момента импульса

Вращение твердых тел удобно характеризовать физической величиной, которая называется моментом импульса.

При вращении твердого тела вокруг неподвижной оси каждая отдельная частица тела движется по окружности радиусом r_i с какой-то линейной скоростью v_i. Скорость v_i и импульс p = m_iv_i перпендикулярны радиусу r_i. Произведение импульса p = m_iv_i на радиус r_i называется моментом импульса частицы:

^Li = ^mi ^vi ^ri = ^Pi ^ri ·

Момент импульса всего тела:



Если заменить линейную скорость угловой щ (v_i = ωr_i), то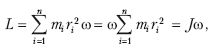



где J = mr²– момент инерции.

Момент импульса замкнутой системы не изменяется во времени, то есть L = const и Jω = const.

При этом моменты импульса отдельных частиц вращающегося тела могут как угодно изменяться, однако общий момент импульса (сумма моментов импульса отдельных частей тела) остается постоянным. Продемонстрировать закон сохранения момента импульса можно, наблюдая вращение фигуриста на коньках с руками, вытянутыми в стороны, и с руками, поднятыми над головой. Так как Jω = const, то во втором случае момент инерции J уменьшается, значит, при этом должна возрасти угловая скорость щ, так как Jω = const.

Закон сохранения энергии

Энергия – это универсальная мера различных форм движения и взаимодействия. Энергия, отданная одним телом другому, всегда равна энергии, полученной другим телом. Для количественной оценки процесса обмена энергией между взаимодействующими телами в механике вводится понятие работы силы, вызывающей движение.

Кинетическая энергия механической системы – это энергия механического движения этой системы. Сила, вызывающая движение тела, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Как известно, тело массой m, движущееся со скоростью v, обладает кинетической энергией E = mv²/2.

Потенциальная энергия – это механическая энергия системы тел, которые взаимодействуют посредством силовых полей, например посредством гравитационных сил. Работа, совершаемая этими силами, при перемещении тела из одного положения в другое не зависит от траектории движения, а зависит только от начального и конечного положения тела в силовом поле.

Такие силовые поля называют потенциальными, а силы, действующие в них, – консервативными. Гравитационные силы являются консервативными силами, а потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна

Е_пот = mgh,

где g – ускорение свободного падения.

Полная механическая энергия равна сумме кинетической и потенциальной энергии:

E = Е_кин + Е_пот

Закон сохранения механической энергии (1686 г., Лейбниц) гласит, что в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется неизменной во времени. При этом могут происходить превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах.

Существуют еще один вид систем, в которых механическая энергия может уменьшаться за счет преобразования в другие формы энергии. Например, при движении системы с трением часть механической энергии уменьшается за счет трения. Такие системы называются диссипативными, то есть системами, рассеивающими механическую энергию. В таких системах закон сохранения полной механической энергии несправедлив. Однако при уменьшении механической энергии всегда возникает эквивалентное этому уменьшению количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. Здесь проявляется свойство неуничтожимости материи и ее движения.

Закон сохранения заряда

Электрические заряды – это источники электромагнитного поля. Вся совокупность электрических явлений есть проявление существования движения и взаимодействия электрических зарядов.

В конце XIX в. английским физиком Томсоном был открыт электрон – носитель отрицательного элементарного электрического заряда (-1,6 · 10^-19 Кл), а в начале XX в. Резерфорд открыл протон, обладающий таким же по величине элементарным положительным зарядом. Поскольку каждая частица характеризуется определенным, присущим ей электрическим зарядом, закон сохранения заряда можно рассматривать как следствие сохранения числа частиц, если при этом не происходит взаимопревращения частиц.

При электризации физических тел число заряженных частиц не меняется, а происходит лишь их перераспределение в пространстве. В общем закон сохранения заряда можно сформулировать так:

► в замкнутой системе алгебраическая сумма зарядов системы остается неизменной во времени, какие бы процессы ни происходили внутри этой замкнутой системы.

Такое понятие существовало в физике давно, а в 1843 г. М. Фарадей экспериментально подтвердил этот закон. Как и другие законы сохранения, закон сохранения заряда справедлив на всех структурных уровнях материального мира.

Закон сохранения заряда вместе с законом сохранения энергии характеризует устойчивость электрона. Он не может превратиться самопроизвольно в более тяжелую частицу или в более легкую.

В первом случае это не позволяет закон сохранения энергии, а во втором – закон сохранения заряда.

3.3. Принципы современной физики

Принцип симметрии

Под симметрией понимают однородность, пропорциональность, гармонию каких-то материальных объектов. Асимметрия – понятие противоположное. Любой физический объект содержит элементы симметрии и асимметрии. Рассмотрим симметрии в физике, химии и биологии.

В физике симметрия определяется следующим образом: если физические законы не меняются при определенных преобразованиях, которым может быть подвергнута система (физический объект), то считается, что эти законы обладают симметрией (или инвариантны) относительно этих преобразований.

Симметрии делят на пространственно-временные и внутренние, последние относятся только к микромиру.

Среди пространственно-временных рассмотрим основные.

1. Сдвиг времени. Изменение начала отсчета не изменяет физических законов. Время однородно по всему пространству.

2. Сдвиг системы отсчета пространственных координат. Такая операция не изменяет физических законов. Все точки пространства равноправны, и пространство однородно.

3. Поворот системы отсчета пространственных координат также сохраняет физические законы неизменными – значит, пространство изотропно.

4. Классический принцип относительности Галилея устанавливает симметрию между покоем и равномерным прямолинейным движением.

5. Обращение знака времени не изменяет фундаментальных законов в макромире, то есть процессы макромира могут описываться и при обращении знака времени. На уровне макромира наблюдается необратимость процессов, так как они связаны с неравновесным состоянием Вселенной.

В химии симметрии проявляются в геометрической конфигурации молекул. Это определяет как химические, так и физические свойства молекул. Большинство простых молекул имеют оси симметрии, плоскости симметрии. Например, молекула аммиака NH₃ представляет собой правильную треугольную пирамиду, молекула метана CH₄ – правильный тетраэдр. Представления о симметрии весьма полезны при теоретическом анализе строения комплексных соединений, их свойств и поведения.

В биологии симметрии давно изучаются специалистами. Наибольший интерес представляет структурная симметрия биообъектов. Она проявляется в виде того или иного закономерного повторения. На низших этапах развития живой природы встречаются представители всех классов точечной симметрии (правильные многогранники, шары). На более высоких ступенях эволюции встречаются растения и животные в основном с аксиальной и актиноморфной симметрией. Биообъекты с аксиальной симметрией характеризуются осью симметрии (медуза, цветок флокса), а с актиноморфной – осью симметрии и пересекающимися на этой оси плоскостями (например, бабочка с двусторонней симметрией).

Широко известна симметрия кристаллов. Это свойство кристаллов как бы совмещаться с собой в различных положениях путем поворотов, отражений, параллельных переносов. Симметрия внешней формы кристаллов определяется симметрией их атомного строения.

Все это связано с симметрией физических свойств кристаллов.