Концепции современного естествознания_под ред Михайлова Л.А_Учебник_2008 -336с. Концепции современного естествознания_под ред Михайлова Л.А_Учеб. Учебник для вузов Издательство Питер, 2008 г. 336 стр

• Название: Учебник для вузов Издательство Питер, 2008 г. 336 стр
• Анкор: Концепции современного естествознания_под ред Михайлова Л.А_Учебник_2008 -336с.doc
• Дата: 28.05.2017
• Размер: 2.28 Mb.
• Имя файла: Концепции современного естествознания_под ред Михайлова Л.А_Учеб.doc
• Тип: Учебник; #8195
• страница: 6 из 23

Релятивистские эффекты

Под релятивистскими эффектами в теории относительности понимают изменения пространственно-временных характеристик тел при скоростях, соизмеримых со скоростью света.

В качестве примера обычно рассматривается космический корабль типа фотонной ракеты, который летит в космосе со скоростью, соизмеримой со скоростью света. При этом неподвижный наблюдатель может заметить три релятивистских эффекта:

1. Увеличение массы по сравнению с массой покоя. С ростом скорости растет и масса. Если бы тело могло двигаться со скоростью света, то его масса возросла бы до бесконечности, что невозможно. Эйнштейн доказал, что масса тела есть мера содержащейся в ней энергии (E= mc²). Сообщить телу бесконечную энергию невозможно.

2. Сокращение линейных размеров тела в направлении его движения. Чем больше будет скорость космического корабля, пролетающего мимо неподвижного наблюдателя, и чем ближе она будет к скорости света, тем меньше будут размеры этого корабля для неподвижного наблюдателя. При достижении кораблем скорости света его наблюдаемая длина будет равна нулю, чего быть не может. На самом же корабле космонавты этих изменений не будут наблюдать. 3. Замедление времени. В космическом корабле, движущемся со скоростью, близкой к скорости света, время течет медленнее, чем у неподвижного наблюдателя.

Эффект замедления времени сказался бы не только на часах внутри корабля, но и на всех процессах, протекающих на нем, а также на биологических ритмах космонавтов. Однако фотонную ракету нельзя рассматривать как инерциальную систему, ибо она во время разгона и торможения движется с ускорением (а не равномерно и прямолинейно).

В теории относительности предложены принципиально новые оценки пространственно-временных отношений между физическими объектами. В классической физике при переходе от одной инерциальной системы (№ 1) к другой (№ 2) время остается тем же – t₂ = t_L а пространственная координата изменяется по уравнению x₂ = x₁– vt. В теории относительности применяются так называемые преобразования Лоренца: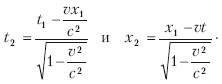



Из отношений видно, что пространственные и временные координаты зависят друг от друга. Что касается сокращения длины в направлении движения, то



а ход времени замедляется: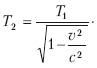



В 1971 г. в США был поставлен эксперимент по определению замедления времени. Изготовили двое совершенно одинаковых точных часов. Одни часы оставались на земле, а другие помещались в самолет, который летал вокруг Земли. Самолет, летящий по круговой траектории вокруг Земли, движется с некоторых ускорением, и значит, часы на борту самолета находятся в другой ситуации по сравнению с часами, покоящимися на земле. В соответствии с законами теории относительности часы-путешественники должны были отстать от покоящихся на 184 нс, а на самом деле отставание составило 203 нс. Были и другие эксперименты, в которых проверялся эффект замедления времени, и все они подтвердили факт замедления. Таким образом, разное течение времени в системах координат, движущихся относительно друг друга равномерно и прямолинейно, является непреложным экспериментально установленным фактом.
Общая теория относительности

После опубликования специальной теории относительности в 1905 г. А. Эйнштейн обратился к современному представлению тяготения. В 1916 г. он опубликовал общую теорию относительности (ОТО), которая с современных позиций объясняет теорию тяготения. Она основывается на двух постулатах специальной теории относительности и формулирует третий постулат – принцип эквивалентности инертной и гравитационной масс. Важнейшим выводом ОТО является положение об изменении геометрических (пространственных) и временных характеристик в гравитационных полях (а не только при движении с большими скоростями). Этот вывод связывает ОТО с геометрией, то есть в ОТО наблюдается геометризация тяготения. Классическая геометрия Евклида для этого не годилась. Новая геометрия появилась еще в XIX в. в трудах русского математика Н. И. Лобачевского, немецкого – Б. Римана, венгерского – Я. Больяйя.

Геометрия нашего пространства оказалась неевклидовой.

ОТО^[3] – физическая теория, в основе которой лежит ряд экспериментальных фактов. Рассмотрим некоторые из них. Гравитационное поле влияет на движение не только массивных тел, но и света. Луч света отклоняется в поле Солнца. Измерения, проведенные в 1922 г. английским астрономом А. Эддингтоном во время солнечного затмения, подтвердили это предсказание Эйнштейна.

В ОТО орбиты планет незамкнуты. Небольшой эффект такого рода можно описывать как вращение перигелия эллиптической орбиты. Перигелий – это ближайшая к Солнцу точка орбиты небесного тела, которое движется вокруг Солнца по эллипсу, параболе или гиперболе. Астрономам известно, что перигелий орбиты Меркурия поворачивается за столетие примерно на 6000». Это объясняется гравитационными возмущениями со стороны других планет. При этом оставался неустранимый остаток около 40» за столетие. В 1915 г. Эйнштейн объяснил это расхождение в рамках ОТО.

Существуют объекты, в которых эффекты ОТО играют определяющую роль. К ним относятся «черные дыры». «Черная дыра» возникает тогда, когда звезда сжимается настолько сильно, что существующее гравитационное поле не выпускает во внешнее пространство даже свет. Поэтому из такой звезды не исходит никакой информации. Многочисленные астрономические наблюдения указывают на реальное существование таких объектов. ОТО дает четкое объяснение этому факту.

В 1918 г. Эйнштейн предсказал на основе ОТО существование гравитационных волн: массивные тела, двигаясь с ускорением, излучают гравитационные волны. Гравитационные волны должны распространяться с той же скоростью, что электромагнитные, то есть со скоростью света. По аналогии с квантами электромагнитного поля принято говорить о гравитонах как о квантах гравитационного поля. В настоящее время формируется новая область науки – гравитационно-волновая астрономия. Есть надежда, что гравитационные эксперименты дадут новые результаты.

На основании уравнений теории относительности отечественный математик-физик А. Фридман в 1922 г. нашел новое космологическое решение уравнений ОТО Это решение указывает на то, что наша Вселенная не стационарна, она непрерывно расширяется. Фридман нашел два варианта решения уравнений Эйнштейна, то есть два варианта возможного развития Вселенной. В зависимости от плотности материи Вселенная или будет и далее расширяться, или через какое-то время начнет сжиматься.

В 1929 г. американский астроном Э. Хаббл экспериментально установил закон, который определяет скорость разлета галактик в зависимости от расстояния до нашей галактики. Чем дальше разбегающаяся галактика, тем больше скорость ее разбегания. Хаббл использовал эффект Доплера, в соответствии с которым у источника света, удаляющегося от наблюдателя, длина волны увеличивается, то есть смещается к красному концу спектра (краснеет).

Таким образом, все известные научные факты подтверждают справедливость общей теории относительности, которая является современной теорией тяготения.

3.6. Начала термодинамики. Представления об энтропии

Общие сведения о термодинамике

► Термолинамика – это наука о наиболее общих свойствах макроскопических тел и систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода из одного состояния в другое.

Классическая термодинамика изучает физические объекты материального мира только в состоянии термодинамического равновесия. Здесь подразумевается такое состояние, в которое с течением времени приходит система, находящаяся при определенных неизменных внешних условиях и определенной постоянной температуре окружающей среды. Для таких равновесных состояний понятие времени несущественно. Поэтому время в явном виде как параметр в термодинамике не используется. В первоначальном виде эта дисциплина называлась «механическая теория тепла». Термин «термодинамика» был введен в научную литературу в 1854 г. В. Томсоном. Равновесные процессы классической термодинамики позволяют также судить о закономерностях процессов, происходящих при установлении равновесия, то есть рассматривает пути к установлению термодинамического равновесия.

Вместе с тем термодинамика рассматривает условия существования необратимых процессов. Например, распространение молекул газа (закон диффузии) ведет в конце концов к равновесному состоянию, а обратный переход такой системы к первоначальному состоянию термодинамика запрещает.

Задачей термодинамики необратимых процессов сначала было изучение неравновесных процессов для состояний, не слишком сильно отличающихся от равновесного. Возникновение термодинамики необратимых процессов относится к 50-м гг. прошлого столетия. Она сформировалась на базе классической термодинамики, которая возникла во второй половине XIX в. В становлении классической термодинамики выдающуюся роль сыграли работы Н. Карно, Б. Клапейрона, Р. Клаузиуса и др. Прошло сравнительно много времени, прежде чем стало понятно, что классическая термодинамика является по существу термостатикой, а основополагающие уравнения Фурье– Ома—Фика и Навье—Стокса представляют собой элементы будущей термодинамики. Здесь следует назвать одного из пионеров нового направления в термодинамике – американского физика Л. Онсагера (Нобелевская премия 1968 г.), а также голландско-бельгийскую школу И. Пригожина, С. де Грота, П. Мазура. В 1977 г. бельгийскому физику и физико-химику русского происхождения Илье Романовичу Пригожину была присуждена Нобелевская премия по химии «за вклад в теорию неравновесной термодинамики, в особенности – в теорию диссипативных структур, и за ее применения в химии и биологии».
Термодинамика как функция состояния

Равенство температур во всех точках каких-то систем или частей одной системы является условием равновесия.

Состояние однородных жидкостей или газа полностью фиксируется заданием любых двух из трех величин: температуры Г, объема V, давления р. Связь между p, V и T называется уравнением состояния. Французский физик Б. Клапейрон в 1934 г. вывел уравнение состояния для идеального газа, объединив законы Бойля-Мариотта и Гей-Люсака. Д. И. Менделеев объединил уравнения Клапейрона с законом Авогадро. Согласно закону Авогадро, при одинаковых давлениях р и температуре Г моли всех газов занимают одинаковый молярный объем V_m, поэтому для всех газов существует молярная газовая постоянная R. Тогда Уравнение Клапейрона—Менделеева можно записать в виде:

pV_m= RT.

Числовое значение молярной газовой постоянной R = 8,31 Дж/моль · K.
Первое начало термодинамики

Первое начало, или первый закон термодинамики, или закон сохранения энергии для тепловых систем, удобно рассмотреть на примере работы тепловой машины. В состав тепловой машины входят источник тепла Q₁, рабочее тело, например цилиндр с поршнем, под которым газ может нагреваться (ΔQ₁) или охлаждаться холодильником, отбирающим от рабочего тела тепло ΔQ₂. При этом может совершаться работа ΔA и изменяется внутренняя энергия ΔU.

Энергия теплового движения может превращаться в энергию механического движения, и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии. Применительно к термодинамическим процессам это и есть первое начало термодинамики, установленное в результате обобщения многовековых опытных данных. Опыт показывает, что изменение внутренней энергии ΔU определяется разностью между количеством теплоты Q₁, полученной системой, и работой А:

ΔU = Q₁– A

или:

Q₁= A₁ + ΔU.

В дифференциальной форме:

dQ = dA + dU.

Первое начало термодинамики определяет вторую функцию состояния – энергию, точнее, внутреннюю энергию U, которая представляет энергию хаотического движения всех молекул, атомов, ионов и т. д., а также энергию взаимодействия этих микрочастиц. Если система не обменивается с окружающей средой энергией или веществом (изолированная система), то dU = 0, а U = const в соответствии с законом сохранения энергии. Отсюда следует, что работа А равна количеству теплоты Q, то есть периодически действующий двигатель (тепловая машина) не может совершать работу большую, чем сообщенная ему извне энергия, а это значит, что невозможно создать двигатель, который путем каких-то преобразований энергии может увеличить ее общее количество.
Круговые процессы (циклы). Обратимые и необратимые процессы

► Круговым процессом (циклом) называется такой процесс, при котором система проходит через ряд состояний и возвращается в исходное состояние. Такой цикл можно представить замкнутой кривой в осях P, V, где P – давление в системе, а V – ее объем. Замкнутая кривая состоит из участков, где объем увеличивается (расширение), и участка, где объем уменьшается (сжатие).

При этом работа, совершаемая за цикл, определяется площадью, охватываемой замкнутой кривой. Цикл, который протекает через расширение, а потом сжатие, называется прямым, он используется в тепловых машинах – периодически действующих двигателях, совершающих работу за счет полученного извне тепла. Цикл, который протекает через сжатие, а потом расширение, называется обратным и используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится от одного тела к другому. В результате кругового процесса система возвращается в исходное состояние:

ΔU =0, Q = A

Система может как получать теплоту, так и отдавать. Если система получает Q₁ теплоты, а отдает Q₂, то термический коэффициент полезного действия для кругового процесса



Обратимые процессы могут происходить как в прямом, так и в обратном направлении

В идеальном случае, если процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде не происходит никаких изменений Обратимые процессы – это идеализация реальных процессов, при которых всегда происходит некоторая потеря энергии (на трение, теплопроводность и т д)

Понятие обратимого кругового процесса ввел в физику в 1834 г французский ученый Б Клапейрон
Идеальный цикл теплового двигателя Карно

Когда мы говорим об обратимости процессов, следует учитывать, что это некоторая идеализация. Все реальные процессы необратимы, поэтому и циклы, по которым работают тепловые машины, также необратимы, а значит и неравновесны. Однако для упрощения количественных оценок таких циклов необходимо считать их равновесными, то есть как если бы они состояли только из равновесных процессов. Этого требует хорошо разработанный аппарат классической термодинамики.

Знаменитый цикл идеального двигателя Карно считается равновесным обратным круговым процессом. В реальных условиях любой цикл не может быть идеальным, так как существуют потери. Он совершается между двумя источниками теплоты с постоянными температурами у теплоотдатчика Т₁ и теплоприемника Т₂, а также рабочим телом, в качестве которого принят идеальный газ (рис. 3.1).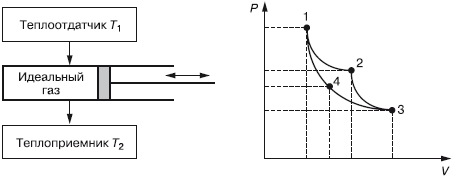




Рис. 3.1. Цикл теплового двигателя
Полагаем, что Т₁ > Т₂ и отвод тепла от теплоотдатчика и подвод тепла к теплоприемнику не влияют на их температуры, T₁ и T₂ остаются постоянными. Обозначим параметры газа при левом крайнем положении поршня теплового двигателя: давление – Р₁ объем – V₁, температура Т₁. Это точка 1 на графике на осях P-V. В этот момент газ (рабочее тело) взаимодействует с теплоотдатчиком, температура которого также Т₁. При движении поршня вправо давление газа в цилиндре уменьшается, а объем увеличивается. Это будет продолжаться до прихода поршня в положение, определяемые точкой 2, где параметры рабочего тела (газа) примут значения P₂, V₂, T₂. Температура в этой точке остается неизменной, так как температура газа и теплоотдатчика одинакова в процессе перехода поршня от точки 1 к точке 2 (расширение). Такой процесс, при котором Т не изменяется, называется изотермическим, а кривая 1–2 называется изотермой. В этом процессе от теплоотдатчика к рабочему телу переходит теплота Q₁.

В точке 2 цилиндр полностью изолируется от внешней среды (теплообмена нет) и при дальнейшем движении поршня вправо уменьшение давления и увеличение объема происходит по кривой 2–3, которая называется адиабатой (процесс без теплообмена с внешней средой). Когда поршень переместится в крайнее правое положение (точка 3), процесс расширения закончится и параметры будут иметь значения Р₃, V₃, а температура станет равной температуре теплоприемника Т₂. При этом положении поршня изоляция рабочего тела снижается и оно взаимодействует с теплоприемником. Если теперь увеличивать давление на поршень, то он будет перемещаться влево при неизменной температуре Т₂ (сжатие). Значит, этот процесс сжатия будет изотермическим. В этом процессе теплота Q₂ перейдет от рабочего тела к тепло-приемнику. Поршень, двигаясь влево, придет в точку 4 с параметрами P₄, V₄ и T₂, где рабочее тело вновь изолируется от внешней среды. Дальнейшее сжатие происходит по адиабате 4–1 с повышением температуры. В точке 1 сжатие заканчивается при параметрах рабочего тела P₁, V₁, T₁. Поршень возвратился в исходное состояние. В точке 1 изоляция рабочего тела от внешней среды снимается и цикл повторяется.

Таким образом, цикл Карно можно считать обратимым. Хотя при этом не учитывались различные сопутствующие потери (тепла в окружающую среду, на трение и некоторые другие условия идеализации).

Коэффициент полезного действия идеального двигателя Карно:



Анализ выражения для КПД цикла Карно позволяет сделать следующие выводы:

1) КПД тем больше, чем больше Т₁ и чем меньше Т₂;

2) КПД всегда меньше единицы;

3) КПД равен нулю при Т₁ = Т₂.

Цикл Карно дает наилучшие использования теплоты, но, как указывалось выше, он является идеализированным и в реальных условиях неосуществим. Однако значение его велико. Он позволяет определить наивысшее значение КПД теплового двигателя.
Второе начало термодинамики. Энтропия

Второе начало термодинамики связано с именами Н. Карно, В. Томсона (Кельвина), Р. Клаузиуса, Л. Больцмана, В. Нернста.

Второе начало термодинамики вводит в рассмотрение новую функцию состояния – энтропию. Термин «энтропия», предложенный Р. Клаузиусом, образован от греч. entropia и означает «превращение».

Уместно будет привести понятие «энтропия» в формулировке А. Зоммерфельда: «Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия; вычисляются все проводимые при этом к системе порции тепла dQ, делятся каждая на соответствующую ей абсолютную температуру Т, и все полученные таким образом значения суммируются (первая часть второго начала термодинамики). При реальных (неидеальных) процессах энтропия изолированной системы возрастает (вторая часть второго начала термодинамики)».

Учета и сохранения количества энергии еще недостаточно для того, чтобы судить о возможности того или иного процесса. Энергию следует характеризовать не только количеством, но и качеством. При этом существенно, что энергия определенного качества самопроизвольно может превращаться только в энергию более низкого качества. Величиной, определяющей качество энергии, и является энтропия.

Процессы в живой и неживой материи в целом протекают так, что энтропия в замкнутых изолированных системах возрастает, а качество энергии понижается. В этом и есть смысл второго начала термодинамики.

Если обозначить энтропию через S,то




что и соответствует первой части второго начала по Зоммерфельду.

Можно подставить выражение для энтропии в уравнение первого начала термодинамики:

dU = T × dS – dU.

Эта формула известна в литературе как соотношение Гиббса. Это фундаментальное уравнение объединяет первое и второе начала термодинамики и определяет, по существу, всю равновесную термодинамику.

Второе начало устанавливает определенное направление течения процессов в природе, то есть «стрелу времени».

Наиболее глубоко смысл энтропии вскрывается при статической оценке энтропии. В соответствии с принципом Больцмана энтропия связана с вероятностью состояния системы известным соотношением

S = K × LnW,

где W – термодинамическая вероятность, а К – постоянная Больцмана.

Под термодинамической вероятностью, или статическим весом, понимается число различных распределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию. При любом процессе, который протекает в изолированной системе и переводит ее из состояния 1 в состояние 2, изменение ΔW термодинамической вероятности положительно или равно нулю:

ΔW = W₂– W₁≥ 0

В случае обратимого процесса ΔW = 0, то есть термодинамическая вероятность, постоянна. Если происходит необратимый процесс, то ΔW > 0 и W возрастает. Это означает, что необратимый процесс переводит систему из менее вероятного состояния в более вероятное. Второе начало термодинамики является статистическим законом, оно описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему, то есть энтропия характеризует меру беспорядочности, хаотичности частиц в системе.

Р. Клаузиус определил второе начало термодинамики так:

► невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому (1850).

В связи с этой формулировкой в середине XIX в. была определена проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему, Р. Клаузиус, опираясь на второе начало термодинамики, утверждал, что рано или поздно энтропия Вселенной должна достигнуть своего максимума. Переход теплоты от более нагретых тел к менее нагретым приведет к тому, что температура всех тел Вселенной будет одинаковой, наступит полное тепловое равновесие и все процессы во Вселенной прекратятся – наступит тепловая смерть Вселенной.

Ошибочность вывода о тепловой смерти Вселенной заключается в том, что нельзя применять второе начало термодинамики к системе, которая является не замкнутой, а бесконечно развивающей системой. Вселенная расширяется, галактики разбегаются со скоростями, которые нарастают. Вселенная нестационарна.

В основу формулировок второго начала термодинамики положены постулаты, являющиеся результатом многовекового человеческого опыта. Кроме указанного постулата Клаузиуса наибольшую известность получил постулат Томсона (Кельвина), который говорит о невозможности построения вечного теплового двигателя второго рода (perpetuum mobile), то есть двигателя, полностью превращающего теплоту в работу. Согласно этому постулату, из всей теплоты, полученной от источника тепла с высокой температурой – теплоотдатчика, только часть может быть превращена в работу. Остальная часть должна быть отведена в теплоприемник с относительно низкой температурой, то есть для работы теплового двигателя необходимы по крайней мере два тепловых источника различной температуры.

Этим и объясняется причина, по которой нельзя перевести в работу теплоту окружающей нас атмосферы или теплоту морей и океанов при отсутствии таких же масштабных источников теплоты с более низкой температурой.
Третье начало термодинамики, или тепловая теория Нернста

Среди функций состояния, кроме температуры Т, внутренней энергии U и энтропии S, имеются и такие, которые содержат произведение T ·S. Например, при изучении химических реакций важную роль играют такие функции состояния, как свободная энергия F = U – T · S или потенциал Гиббса Ф = U+ pV– TS. В эти функции состояния входит произведение T ·S. Однако величина S определяется лишь с точностью до произвольной постоянной S₀, так как энтропия определяется через ее дифференциал dS. Следовательно, без конкретизации S₀ применение функций состояния становится неопределенным. Возникает вопрос об абсолютном значении энтропии.

Тепловая теория Нернста отвечает на этот вопрос. В формулировке Планка она сводится к утверждению: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

limS =0.

Так как энтропия определяется с точностью до аддитивной постоянной S₀, то эту постоянную удобно взять равной нулю.

Тепловая теорема была сформулирована Нерстом в начале XX в. (Нобелевская премия по физике в 1920 г.). Она не вытекает из первых двух начал, поэтому в силу своей общности с полным правом может рассматриваться как новый закон природы – третье начало термодинамики.
Неравновесная термодинамика

Неравновесные системы характеризуются не только термодинамическими параметрами, но и скоростью их изменения во времени и в пространстве, которая определяет потоки (процессы переноса) и термодинамические силы (градиент температуры, градиент концентрации и др.).

Появление потоков в системе нарушает статистическое равновесие. В любой физической системе всегда происходят процессы, старающиеся вернуть систему в состояние равновесия. Происходит как бы противоборство между процессами переноса, нарушающими равновесие, и внутренними процессами, старающимися его восстановить.

Процессы в неравновесных системах обладают следующими тремя свойствами:

1. Процессы, приводящие систему к термодинамическому равновесию (восстановление), происходят тогда, когда нет особых факторов, сохраняющих неравновесное состояние внутри самой системы. Если исходное состояние сильно неравновесно, а на фоне общего стремления системы к равновесию рождаются представляющие большой интерес подсистемы, в которых энтропия локально уменьшается, то возникают локальные подсистемы, где упорядоченность повышается. При этом общее возрастание для всей системы во много раз больше. В изолированной системе локальное уменьшение энтропии, конечно, является временным. В открытой же системе, через которую длительное время протекают мощные потоки, снижающие энтропию, могут возникнуть какие-то упорядоченные подсистемы. Они могут существовать, изменяясь и развиваясь, очень долго (пока не прекратятся питающие их потоки).

2. Рождение локальных состояний с низкой энтропией приводит к ускорению общего роста энтропии всей системы. Благодаря упорядоченным подсистемам вся система в целом движется быстрее ко все более неупорядоченным состояниям, к термодинамическому равновесию.

Наличие упорядоченной подсистемы может в миллионы и более раз ускорить выход всей системы из «благополучного» метастабильного состояния. В природе ничего «даром» не дается.

3. Упорядоченные состояния представляют собой диссипативные структуры, которые требуют для своего становления большого притока энергии. Такие системы реагируют на малые изменения внешних условий более чутко и более разнообразно, чем термодинамическое равновесное состояние. Они могут легко разрушаться или же превращаться в новые упорядоченные структуры.

Возникновение диссипативных структур носит пороговый характер. Неравновесная термодинамика связала пороговый характер с неустойчивостью. Новая структура всегда является результатом неустойчивости и возникает из флуктуации.

Выдающейся заслугой неравновесной термодинамики является установление того, что самоорганизация присуща не только «живым системам». Способность к самоорганизации является общим свойством всех открытых систем, у которых возможен обмен энергией с окружающей средой. При этом именно неравновесность служит источником упорядоченности.

Этот вывод является основным тезисом для круга идей группы И. Пригожина.

Совместимость второго начала термодинамики со способностью систем к самоорганизации – одно из крупнейших достижений современной неравновесной термодинамики.
Энтропия и вещество. Изменение энтропии в химических реакциях

При повышении температуры растет скорость различных видов движения частиц. Отсюда число микросостояний частиц, а соответственно и термодинамическая вероятность W, и энтропия вещества растут. При переходе вещества из твердого состояния в жидкое увеличивается неупорядоченность частиц и соответственно энтропия (ΔS_плавл). Особенно резко растет неупорядоченность и соответственно энтропия при переходе вещества из жидкого состояния в газообразное (AS_кипен). Энтропия увеличивается при превращении кристаллического вещества в аморфное. Чем выше твердость вещества, тем меньше его энтропия. Увеличение атомов в молекуле и усложнение молекул ведет к увеличению энтропии. Энтропия измеряется в Кал/моль·К (энтропийная единица) и в Дж/моль·К При расчетах применяют значения энтропии в так называемом стандартном состоянии, то есть при 298,15 К (25 °C). Тогда энтропию обозначают S⁰₂₉₈. Например, энтропия кислорода 0₃ – S⁰₂₉₈ = 238,8 ед. э., а 0₂ – S⁰₂₉₈ = 205 ед. э.

Абсолютные значения энтропии многих веществ являются табличными и приведены в справочниках. Например:

Н₂0(ж) = 70,8; Н₂0(г) = 188,7; СО(г) = 197,54;

СН₄(r) = 186,19; Н₂(г) = 130,58; НС1(г) = 186,69; НСl(р) = 56,5;

СН₃0Н(ж) = 126,8; Са(к) = 41,4; Са(ОН)₂(к) = 83,4; С(алмаз) = 2,38;

С(графит) = 5,74 и т. д.

Примечание: ж – жидкость, г – газ, к – кристаллы; р – раствор.

Изменение энтропии системы в результате химической реакции (ΔS) равно сумме энтропий продуктов реакции за вычетом энтропий исходных веществ. Например:

СН₄ +Н₂0(г) = С0 + 3Н₂– здесь ΔS⁰₂₉₈ = S⁰_co.298 + 3S⁰_H2.298 – S⁰_H4.298 – S⁰_H2.298 =

197,54 = 3 · 130,58 – 188,19 – 188,7 = 214,39 Дж/моль · К.

В результате реакции энтропия возросла (AS > 0), возросло число молей газообразных веществ.
Информационная энтропия. Энтропия в биологии

Информационная энтропия служит мерой неопределенности сообщений. Сообщения описываются множеством величин x₁, x₂ x_n, которые могут быть, например, словами: p₁, p₂…, p_n. Информационную энтропию обозначают S_n или H_u. Для определенного дискретного статистического распределения вероятностей P_i используют следующее выражение:



при условии:



Значение S_n = 0, если какая-либо вероятность P_i = 1, а остальные вероятности появления других величин равны нулю. В этом случае информация достоверна, то есть неопределенность в информации отсутствует. Информационная энтропия принимает наибольшее значение, когда P_i равны между собой и неопределенность в информации максимальна.

Общая энтропия нескольких сообщений равна сумме энтропий отдельных сообщений (свойство аддитивности).

Американский математик Клод Шеннон, один из создателей математической теории информации, использовал понятие энтропии для определения критической скорости передачи информации и при создании «помехоустойчивых кодов». Такой подход (использование из статистической термодинамики вероятностной функции энтропии) оказался плодотворными в других направлениях естествознания.

Понятие энтропии, как показал впервые Э. Шредингер (1944 г.), а затем Л. Бриллюэн и др., существенно и для понимания многих явлений жизни и даже деятельности человека.

Теперь ясно, что с помощью вероятностной функции энтропии можно анализировать все стадии перехода системы от состояния полного хаоса, которому соответствуют равные значения вероятностей и максимальное значение энтропии, к состоянию предельно возможной упорядоченности, которому соответствует единственно возможное состояние элементов системы.

Живой организм с точки зрения протекающих в нем физико-химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, нестационарном состоянии. Для живых организмов характерна сбалансированность процессов обмена, ведущих к уменьшению энтропии. Конечно, с помощью энтропии нельзя охарактеризовать жизнедеятельность в целом, так как жизнь не сводится к простой совокупности физико-химических процессов. Ей свойственны другие сложные процессы саморегуляции.

Вопросы для самопроверки

1. Сформулируйте законы движения Ньютона.

2. Перечислите основные законы сохранения.

3. Назовите общие условия справедливости законов сохранения.

4. Объясните существо принципа симметрии и связь этого принципа с законами сохранения.

5. Сформулируйте принцип дополнительности и принцип неопределенности Гейзенберга.

6. В чем состоит «крушение» лапласовского детерминизма?

7. Как формулируются постулаты Эйнштейна в СТО?

8. Назовите и объясните релятивистские эффекты.

9. В чем состоит суть ОТО?

10. Почему невозможен вечный двигатель первого рода?

11. Объясните понятие кругового процесса в термодинамике и идеальный цикл Карно.

12. Объясните понятие энтропии как функцию состояния системы.

13. Сформулируйте второе начало термодинамики.

14. Объясните суть понятия «неравновесная термодинамика».

15. Как качественно определяется изменение энтропии при химических реакциях?