Лекция САПР. Лекции САПР систем ЭЛС. Учебник для вузов. М Издво мгту им. Баумана, 2002, 336 с. Теоретические основы сапр Учебник для вузов Корячко В. П., Корейчик В. М., Норенков И. П. М. Энергоатомиздат, 1987, 400 с
 Скачать 412 Kb. Скачать 412 Kb.
|
Объем памяти для хранения графического изображения формата А4, Мб
Для экономии дискового пространства при хранении графических изображений применяются различные методы сжатия данных (например, compressed TIFF). Сжатие файлов не снижает объема оперативной памяти, необходимой для загрузки файла. Сканирование. Сканируемое изображение освещается белым светом от протяженного осветителя и считывается многоэлементными фотоприемными линейками (число фотоприемников в линейке – 2000 и выше). Напряжение на фотоэлементе преобразуется в цифровую форму. Для сканирования цветных изображений используется цветовая модель RGB (Red – Green – Blue). Сканируемое изображение освещается через вращающийся RGB-светофильтр или от трех цветных ламп. Сигнал по каждому основному цвету обрабатывается отдельно. Оптическое разрешение сканера определяется количеством элементов в фотоприемной линейке (обычно < 400 или 300 точек на дюйм). Более высокие разрешения (600, 800, 1600 т/д) достигаются благодаря интерполяции (логическое разрешение), сглаживающей неровности контуров, которые получались бы при простом масштабировании. Синтез изображений методом обратного трассирования лучей Название "трассирование лучей" происходит от слова "путь" (трасса), что связано с моделированием геометрического пути каждого светового луча, участвующего в построении изображения. Процесс моделирования основывается на законах геометрической оптики (законы преломления, отражения, прямолинейности, обратимости хода световых лучей и др.). Основная идея метода сводится к повторению на ЭВМ всех геометрических преобразований, которые совершил бы каждый световой луч на пути источник – объект – приемник. Действительных лучей бесконечно много, для построения изображения достаточно рассмотреть лучи, попадающие в центр рецепторов или исходящие из ограниченного числа точек на изображаемой поверхности. Рецептор (по словарю) – концевые образования чувствительных нервных волокон, воспринимающие раздражения из внешней среды и преобразующие энергию раздражителей в возбуждение, передаваемое в центральную нервную систему. В нашем случае рецептор – точка на экране монитора, участвующая в синтезе изображений. На основании закона обратимости хода световых лучей можно синтезировать путь луча как в направлении объект – изображение, так и в обратном. Поэтому различается два способа трассирования лучей: прямое и обратное. При прямом трассировании за исходную позицию берут точку 2 на изображаемой поверхности и моделируют путь луча из нее на источник света 3 и на приемник изображения 1. При обратном трассировании за исходную позицию берут центр рецептора на приемнике изображения 1 и моделируют путь луча из него на объект 2 и далее от объекта на источник света 3.          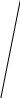  объект 3 2 1          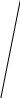  объект 3 2 1     При синтезировании изображения методом трассирования лучей используются следующие понятия и системы координат. Сцена – совокупность изображаемых объектов. Объект – совокупность точек пространства, объединенных функциональной общностью. 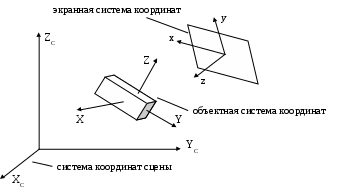 Для того, чтобы моделировать масштаб и ракурс, экранная система должна управляемо перемещаться и переориентироваться в объектной системе координат. Это делается с помощью матриц преобразования, связывающих объектную и экранную системы координат, в которых учитывается взаимное расположение систем координат с помощью углов и . 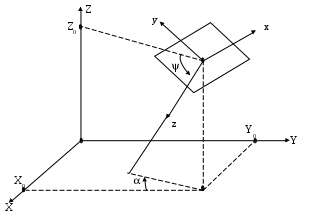 Этапы метода: – определение пространственного положения любого рецептора; – определение точек пересечения светового луча с объектом; – определение видимых точек; – определение затененности-освещенности каждой точки. Наиболее удобно представлять трехмерные объекты для метода обратного трассирования лучей в виде комбинации объемных или плоских примитивов, которые объединяются в блоки. Поверхности примитивов описываются функциями первого и второго порядка. Выбор таких функций обусловлен необходимостью аналитического, а не численного решения уравнений пересечения светового луча с поверхностями. Возможные операции над примитивами мы уже рассмотрели. При трассировании лучей световая прямая пересекается с множеством поверхностей различных примитивов. Прежде всего следует установить факт принадлежности очередной точки пересечения луча поверхности объекта. Этот факт зависит от взаимного расположения точки и примитивов и правила пространственного комбинирования примитивов (см. функцию принадлежности). Для определения освещенности изображения необходимо установить для каждого рецептора, какую точку объекта он "видит", для чего решаются следующие задачи: определение точек пересечения светового луча с примитивом или комбинацией примитивов, а также определение затененных точек. 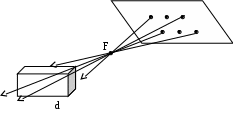 Система уравнений, описывающих эту задачу, может: вообще не иметь решений (луч проходит около поверхности); иметь единственное решение (луч пересекает плоскость или касается выпуклой поверхности), иметь несколько решений (луч пересекает кривую поверхность несколько раз) и бесконечное множество решений (луч совпадает с поверхностью). Последняя группа решений исключается из рассмотрения из-за неопределенности положения точки пересечения. В результате определения пересечения светового луча с примитивом устанавливается сам факт наличия пересечения и вычисляются координаты двух точек пересечения. Одновременно запоминаются номера поверхностей внутри описания примитива, которым эти точки принадлежат. После того как задача определения точек пересечений решена для всех примитивов, входящих в состав объекта, путем преобразования матрицы координат точек пересечения и матрицы номеров поверхностей, которым принадлежат эти точки, среди всей этой совокупности точек выделяется точка, ближайшая к наблюдателю, т.е. видимая. Формально ближайшая точка может не принадлежать поверхности объекта, как это бывает для ближних к наблюдателю вычитающихся примитивов, поэтому после выделения ближайшей точки следует убедиться в том, что она принадлежит поверхности объекта. Для этого сначала с помощью функции принадлежности оценивается положение точки по отношению к каждому примитиву, входящему в состав объекта, а затем по формальным правилам и табл. 1 устанавливается относительное положение точки и объекта. 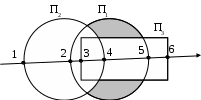 Например, пусть объект составлен из примитивов О = (П1 – П2) – П3. Световой луч пересекает эту комбинацию в точках 1 – 6. Ближайшей к источнику луча (т.е. к экрану) будет точка 1. Функции принадлежности этой точки и примитивов принимают значения: (X1, Y1, Z1; П1) = –1, (X1, Y1, Z1; П2) = 0, (X1, Y1, Z1; П3) = –1, тогда (X1, Y1, Z1; П1 – П2) = –1, (X1, Y1, Z1; (П1 – П2) – П3) = –1. Следовательно, точка 1, будучи ближайшей к источнику луча, не является видимой, так как находится вне объекта. Подобным образом анализируются остальные точки и так до исчерпания всех точек. Таким образом, либо констатируется факт непересечения луча и объекта, либо определяются координаты видимой точки. Множество точек объекта, видимых множеством рецепторов, качественно различается между собой. Одни точки освещаются прямыми лучами света, другие – находятся в тени. Алгоритм вычисления освещенности для этих групп точек существенно отличается, поэтому сначала следует установить признак освещенности – затененности для каждой видимой точки. Видимая точка находится "на свету", если она не загораживается от источника другими поверхностями, т.е. является ближайшей к источнику света среди всех остальных, лежащих на световом луче. При изменении ракурса и положения источника света координаты видимых точек не меняются, изменяется лишь их затененность-освещенность. |
