Учебник по физике магнетизма. Учебник по физике кгтукхти. Кафедра физики. Старостина И. А., Кондратьева О. И., Бурдова Е. В. Для перемещения по тексту электронного учебника можно использовать
 Скачать 1.01 Mb.
|
2.2. Атом в магнитном поле. @Рассмотрим влияние внешнего магнитного поля на движение электронов в атомах вещества. При внесении атома любого вещества в магнитное поле каждый электрон продолжает двигаться по своей орбите, образуя орбитальный ток. Однако теперь на этот ток, как на рамку с током, действует вращательный момент. Это приводит к тому, что электронная орбита приобретает дополнительное вращение. Частота данного вращения зависит только от величины приложенного поля и отношения заряда электрона к его массе: 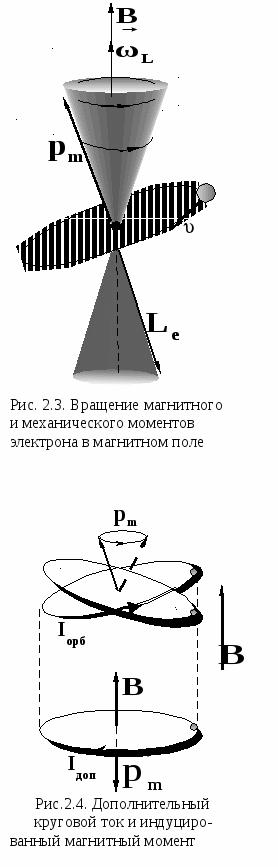 Отсюда следует, что под влиянием внешнего магнитного поля связанные с электронной орбитой векторы  вращаются с той же самой угловой частотой ωL. При этом они описывают круговые конические поверхности с общей вершиной в центре орбиты электрона О вокруг оси, параллельной направлению индукции магнитного поля В (рис.2.3). Частота ωL называется Ларморовой частотой, а возникающее под действием поля дополнительное движение орбиты электрона называется Ларморовой прецессией. Все вышеизложенное составляет суть теоремы Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и магнитного момента электрона с угловой скоростью ωL вокруг оси, проходящей через ядро атома и параллельной вектору В. Сэр Джозеф Лармор, английский физик и математик, доказал эту теорему в 1895 г., еще до того, как стало известно строение атома. Ларморова частота ωL одинакова для всех электронов, входящих в атом.Дополнительное движение электронной орбиты обуславливает дополнительное движение электрона, которому соответствует дополнительный круговой ток, направленный в другую сторону по сравнению с орбитальным током(рис. 2.4): Э   тот ток создает свой магнитный момент  . Дополнительный магнитный момент направлен в сторону, противоположную магнитному полю. Он называетсяиндуцированным, или наведенным магнитным моментом. Среднее значение дополнительного магнитного момента:З  нак «минус» указывает на то, что векторы и  противоположны. Так как электронные микротоки существуют в каждом веществе, то Ларморова прецессия возникает у всех без исключения веществ.2.3. Намагниченность вещества. @Ранее мы предполагали, что провода, несущие ток и создающие магнитное поле, находятся в вакууме. Если же провода находятся в какой-либо среде, то величина создаваемого ими магнитного поля изменится. Это объясняется тем, что всякое вещество, всякая среда способна под действием магнитного поля приобретать магнитный момент, т.е. намагничиваться. Поэтому каждое вещество является магнетиком. Благодаря орбитальным магнитным моментам электронов в атомах, вещество создает свое собственное магнитное поле  , которое накладывается на внешнее поле  . Согласно принципу суперпозиции полей оба поля в сумме дают результирующее поле: Это усредненное (макроскопическое) поле, действующее в веществе. Если внешнее поле отсутствует ( = 0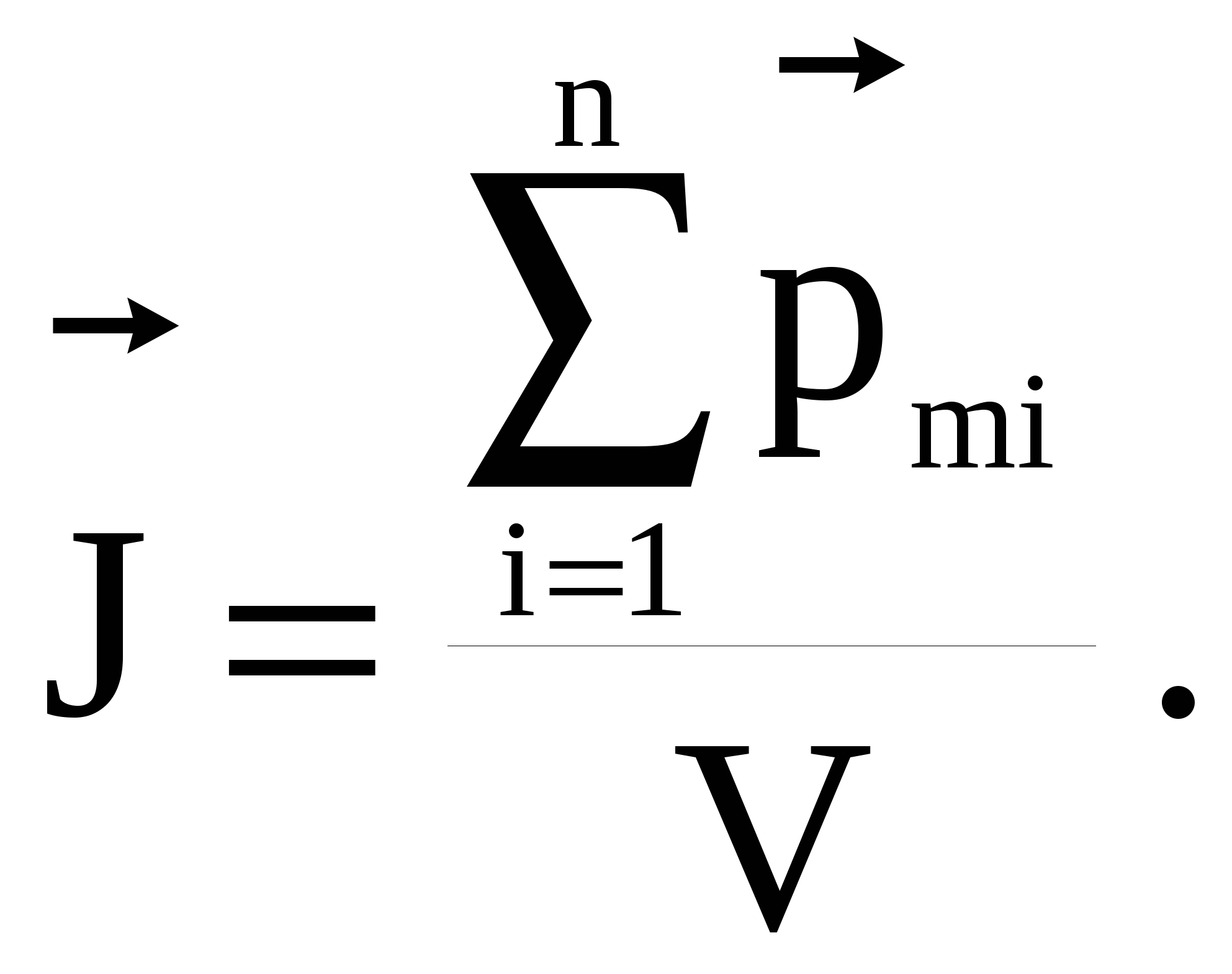), то молекулярные токи чаще всего ориентированы беспорядочным образом, ориентация магнитных моментов отдельных молекул хаотична, и поэтому создаваемое ими собственное поле также равно нулю. Под действием внешнего поля ( ≠ 0) магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего суммарный магнитный момент  уже не равен нулю, и магнетик намагничивается, возникает поле . Количественной характеристикой намагниченного состояния вещества служит векторная величина - намагниченность J, равная отношению магнитного момента некоторого малого объема вещества к этому объему. Другими словами, намагниченность - это магнитный момент единицы объема вещества:П  олученный нами ранее закон полного тока для магнитного поля в вакууме легко обобщить на случай магнитного поля в веществе. В вакууме поля создаются обычными токами проводимости - макротоками, а в веществе – макротоками и микротоками (токами Ампера). Следовательно, для поля в веществе мы можем записать г 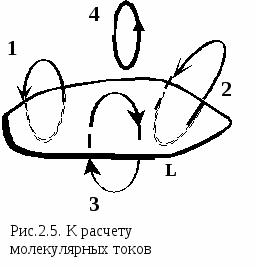  де Iмакро и Iмикро – это алгебраические суммы соответствующих токов, охватываемых замкнутым контуром L. В алгебраическую сумму молекулярных токов входят токи, “нанизанные” на контур, как бусы на нитку (рис.2.5). По рисунку это токи 1 и 2. Прочие токи либо не пересекают поверхность совсем (ток 4), либо пересекают ее дважды – сначала в одном направлении, затем в противоположном (ток 3). Результирующий вклад таких токов равен нулю. Расчет показал, что сумма микротоков, охватываемых замкнутым контуром, равна циркуляции вектора намагниченности вдоль этого контура:  Теперь выражение для вектора циркуляции магнитной индукции можно переписать в другом виде:  Разделим обе части равенства на μ0 :  . Отсюда, объединив интегралы, получим  Вектор  обозначается буквой  и называется напряженностью магнитного поля.Итак, мы получили  . Это уравнение является обобщенным законом полного тока для магнитного поля в веществе: циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура равна сумме всех токов сквозь поверхность, ограниченную этим контуром. Напряженность магнитного поля является аналогом электрического смещения  .В несильных магнитных полях, согласно опытным данным, намагниченность вещества прямо пропорциональна напряженности поля, вызывающего это намагничивание: г  де χ – безразмерная, характерная для данного магнетика величина, называемая магнитной восприимчивостью. Она может принимать для различных веществ как положительные, так и отрицательные значения. Распишем подробнее выражение для напряженности магнитного поля  , отсюда  Величина (1+ χ) также безразмерна, обозначается буквой μ и называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. Итак,  т.е. модуль Н в μμ0 раз меньше модуля В. Для вакуумамагнитная проницаемость μ=1, поэтому  то есть напряженность магнитного поля характеризует магнитное поле в вакууме подобно величине B0.Горные породы земной поверхности по-разному намагничиваются в магнитном поле Земли. Это приводит к возникновению так называемых магнитных аномалий - областей, для которых наблюдаются отклонения векторов напряженности магнитного поля в данном месте земной поверхности от нормальных значений. Магнитные аномалии используются при поисках многих полезных ископаемых, прежде всего сильномагнитных, а также для составления геологических карт. При поиске и разведке месторождений полезных ископаемых применяется метод разведочной геофизики - магнитная разведка. Метод основан на различии магнитных свойств горных пород. На различии магнитной восприимчивости разных веществ (компонентов руды) основан способ обогащения полезных ископаемых, который называется методом магнитной сепарации. Это основной способ обогащения железных руд. |