Учебник по физике магнетизма. Учебник по физике кгтукхти. Кафедра физики. Старостина И. А., Кондратьева О. И., Бурдова Е. В. Для перемещения по тексту электронного учебника можно использовать

• Название: Учебник по физике кгтукхти. Кафедра физики. Старостина И. А., Кондратьева О. И., Бурдова Е. В. Для перемещения по тексту электронного учебника можно использовать
• Анкор: Учебник по физике магнетизма.doc
• Дата: 12.12.2017
• Размер: 1.01 Mb.
• Имя файла: Учебник по физике магнетизма.doc
• Тип: Учебник; #10953
• страница: 5 из 14

1. 8. Рамка с током в однородном магнитном поле. @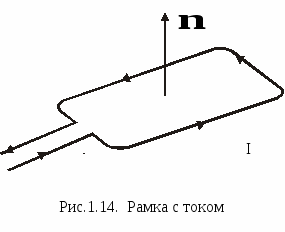

При исследовании магнитного поля часто используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих данное поле. Ориентация контура в пространстве определяется направлением нормали к контуру (рис.1.14). Нормаль строится по правилу правого винта: если головку винта вращать в направлении тока, то движение его острия совпадает с направлением n. На каждый элемент тока в рамке действует сила Ампера, и под действием этой силы магнитное поле поворачивает рамку таким образом, чтобы нормаль к ней располагалась вдоль линий магнитной индукции В. Кстати, так же располагается и стрелка компаса (рис.1.15). Рассчитаем силы, действующие на каждую из четырех сторон рамки. Для простоты будем считать, что стороны в и d перпендикулярны В (рис.1.16 а). Силы 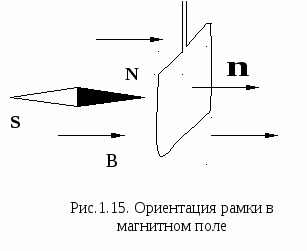и , приложенные к проводникам а и с, численно равны и направлены вдоль вертикальной оси рамки в противоположные стороны, поэтому они полностью уравновешивают друг друга: F₂ =F₄=IaB.

Силы и , действующие на прямолинейные проводники в и d, направлены перпендикулярно плоскости рисунка в противоположные стороны (на рис.4.16 б показан вид рамки сверху) и по закону Ампера численно равны: Силы и создают вращающий момент , который поворачивает рамку. Модуль этого вектора М = 2F₁l, где l =аsinβ (β – угол между направлением магнитной индукции поля В и нормалью к рамке). Воспользовавшись вышеприведенным выражением для силы F₁, получим М = 2IaВsinβ = ISBsinβ, где S = ab- площадь рамки.

Данную формулу можно преобразовать, введя понятие магнитного момента рамки с током (или контура с током).

Магнитным моментом плоского замкнутого кон тура с током I называется вектор 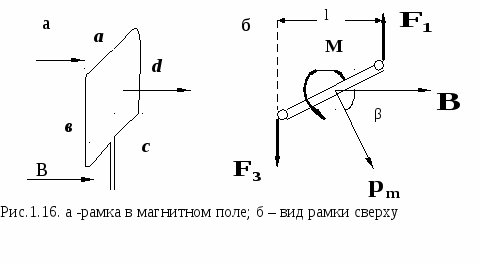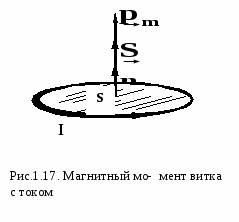, где S – площадь поверхности, ограниченной контуром (ее называют также поверхностью, натянутой на контур);– единичный вектор нормали к плоскости контура.




Векторы направлены перпендикулярно плоскости контура так, что из их концов ток в контуре виден идущим против часовой стрелки (рис.1.17). Для момента сил получаем , модуль момента сил будет равен М = рmBsinβ .

Действие магнитного поля на рамку с током широко применяется в электроизмерительных приборах. Работа любого прибора магнитоэлектрической системы (например, зеркального гальванометра) основана на взаимодействии магнитного поля постоянного магнита и рамки с током. Как известно, в данном случае возникает вращающий момент, который будет поворачивать рамку. Угол поворота рамки и связанные с ним показания шкалы прибора будут зависеть от силы тока в рамке. Такие гальванометры могут измерять постоянные токи порядка 10-11 А.

2. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. @

2.1. Магнитные моменты атомов. @

Д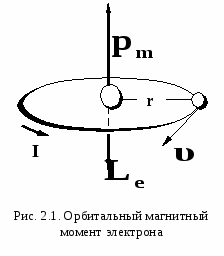ля полного описания атома необходимы знания квантовой механики, которую мы будем изучать позднее. Однако магнитные свойства вещества хорошо объясняются с помощью простой и наглядной планетарной модели атома, предложенной Э.Резерфордом. По Резерфорду атом состоит из положительно заряженного ядра, вокруг которого по своим орбитам движутся отрицательно заряженные электроны. В целом система электрически нейтральна, так как заряд ядра равен суммарному заряду всех электронов в атоме. Согласно представлениям классической физики, электроны в атоме движутся по замкнутым круговым орбитам с постоянной скоростью, образуя систему замкнутых орбитальных токов. Данные токи называются токами Ампера, поскольку Ампер впервые сделал предположение об их существовании. Каких магнитных эффектов можно ожидать в такой системе?

Орбитальному току так же, как и в случае витка и рамки с током, соответствует магнитный момент , называемый орбитальным магнитным моментом электрона. Он направлен из центра орбиты электрона перпендикулярно ее плоскости (как и магнитный момент витка с током), а его модуль рm= IS = Iπr², где r - радиус орбиты электрона; S – площадь орбиты. Если электрон движется по круговой орбите со скоростью υ (рис. 2.1), то сила орбитального тока I=q/t=e/Teν, где T – время одного оборота электрона по орбите, т.е. период; ν – частота вращения электрона по орбите, т.е. число оборотов электрона вокруг ядра за 1 с. Отсюда получаем , откуда и

Равномерно вращаясь по своей орбите, электрон обладает механическим моментом импульса Le, определяемым относительно центра его орбиты (рис. 2.1). Такой момент импульса называется орбитальным. По определению . Численное значение орбитального момента импульса: Le= mυr sin(υ,r) = mυr, так как угол между векторами равен 90°. Вектор Le противоположен по направлению рm, поскольку скорость электрона и ток имеют противоположное направление, однако эти векторы лежат на одной прямой. Поэтому можно записать

М
инус в формуле появляется из-за того, что векторы противоположны. Величина γ называется гиромагнитным или магнитомеханическим отношением орбитальных моментов электрона. Это отношение одинаково для любых по форме и размеру орбит и любых скоростей движения электрона. Однако опыты Эйнштейна и де Гааза, проведенные с железными стержнями, привели к неожиданным результатам. Определенное ими экспериментально гиромагнитное отношение оказалось в два раза больше теоретического! Этот результат имел огромное значение для всего дальнейшего развития физики. Для его объяснения было предположено (а затем и доказано), что электрон кроме обладает собственным моментом импульса, который не имеет ничего общего с его движением по орбите. Этот собственный момент импульса был назван спином электрона (от англ. spin - вращаться). Спин электрона является его квантовым свойством, он неизменен, и с ним связаны многие важные закономерности, например распределение электронов в атоме по оболочкам. Спину соответствует собственный магнитный момент электрона, также имеющий неизменную величину. Векторы магнитного и спинового моментов антипараллельны, как показано на рис.2.2., а отношение их оказывается в два раза больше, чем в случае движения электрона по орбите, т.е. γ_s= -e/m.

Что касается магнитного момента самого ядра, то в большинстве случаев им можно пренебречь, потому что, благодаря своей значительной массе, ядро движется гораздо медленнее электрона, и его магнитный момент в тысячи раз меньше, чем у электрона. Для атома, содержащего больше одного электрона, орбитальным магнитным моментом называется вектор, равный геометрической сумме орбитальных магнитных моментов всех электронов в атоме: . Полный магнитный момент атома складывается из геометрической суммы орбитальных и спиновых моментов всех электронов в атоме: