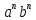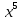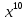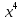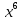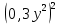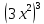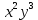математический диктант. алгебра 7 класс диктант. Учебнику по алгебре
 Скачать 28.76 Kb. Скачать 28.76 Kb.
|
|
Математические диктанты к учебнику по алгебре под редакцией С.А. Теляковского (авторы Ю.Н. Макарычев и др.) 7 класс Для чего нужны диктанты Математический диктант как одна из форм обучения и контроля знаний и умений широко применяется учителями математики как на уроках алгебры, так и на уроках геометрии. Одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из различных имеющихся в нашем распоряжении каналов информации слуховой канал занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Это пригодится им в жизни – умение слушать лекцию, слушать собеседника. Кроме того, важно формировать у обучающихся грамотную и точную математическую речь. Математические диктанты необходимо использовать систематически. Если детей приучить с 5 класса, то постепенно они привыкнут к такой форме работы. Виды диктантов Диктанты составленные только из теоретических вопросов; Диктанты, часть которых – теоретические вопросы, а часть простейшие практические задания; Диктанты, состоящие полностью из практических заданий; Словарные диктанты. Как оформить диктант Ответы на вопросы диктантов можно записывать на бланках ответов.
Как оценивать диктанты Оценки за работу выставляются с учетом числа верных выполненных заданий.
Диктанты 7 класс Тема «Выражения» Вариант 1 Запишите пример числового выражения. Найдите значения выражения: 9,6-3*1,2. Запишите в виде выражения: сумма числа 7 и частного чисел 30 и 5. Запишите в виде выражения: квадрат числа х. Найдите значение выражения: 5a-8? Если a = - 2. Напишите формулу четного числа. При каких значения переменной не имеет смысла выражение: 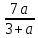 . .Напишите пример строгого неравенства. Запишите в виде неравенства: y – неотрицательное число. Запишите в виде двойного неравенства: 0,47 больше 0,4 и меньше 0,5. Как читается знак «≥». Сравните х+3 и 3х, при х = 2. Вариант 2 Запишите пример выражения с переменными. Найдите значения выражения: 2*1, 7 + 3,6. Запишите в виде выражения: разность произведения 2 и 4 и числа 8. Запишите в виде выражения: куб числа y. Найдите значение выражения 10 – 3х, если х = -3. При каких значениях переменной не имеет смысла выражение: 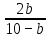 . .Напишите формулу нечетного числа. Запишите в виде неравенства: х – отрицательное число. Напишите пример нестрогого неравенства. Запишите в виде двойного неравенства: 1,6 больше 0,9 и меньше 2,1. Как читается знак «≤». Сравните 5y и y – 2 при y=3. Ответы
Тема «Тождества» Вариант 1 1. Запишите переместительное свойство умножения. 2. Запишите сочетательное свойство сложения 3. Запишите распределительное свойство умножения относительно сложения. 4. Чему равна сумма двух противоположных чисел? Запишите тождество. 5. Продолжите тождество : a*(-b)=… 6. Продолжите тождество : a+0=… 7. Раскройте скобки : 3 – (x-y-z). 8. Приведите подобные слагаемые : a-3+6a. 9. Какие выражения называются тождественно равными? Вариант 2 1. Запишите распределительное свойство умножения относительно вычитания. 2. Запишите переместительное свойство сложения. 3. Запишите сочетательное свойство умножения. 4. Чему равно произведение числа на нуль? Запишите тождество. 5. Продолжите тождество : a*1=… 6. Продолжите тождество: (-а) * (-b)=… 7. Приведите подобные слагаемые : 5y-y+1. 8. Раскройте скобки : 9+(-a+b-c). 9. Какое равенство называется тождеством? Ответы
Тема «Уравнения» Вариант 1 1. Как найти неизвестный множитель? 2. Как найти неизвестное уменьшаемое? 3. Как найти неизвестный делитель? 4. Дайте определение корня уравнения. 5. какое уравнение называется линейным? 6. В каком случае уравнение ax=b имеет бесконечно много корней? 7. Является ли 5 корнем уравнения 2x+3=18? 8. В каком случае уравнение ax=b не имеет корней? 9. Запишите первое свойство уравнений. Вариант 2 1. Как найти неизвестное слагаемое ? 2. Как найти неизвестное делимое ? 3. Как найти неизвестное вычитаемое ? 4. Что значит «решить» уравнение? 5. Какие уравнения называется равносильными? 6. В каком случае уравнение ax=b имеет единственное решение? 7. Является ли 2 корнем уравнения 11-3y=6? 8. Приведите пример линейного уравнения с одной переменной. 9. Запишите второе свойство уравнений. Ответы
Словарный диктант Тема «Выражения, тожества, уравнения» Запишите математические термины
Тема «Определение функции» Вариант 1 1. Дайте определение линейной функции. 2. Как расположен график линейной функции y=kx, если k <0. 3. Функция задана формулой у=3х-7. Найдите значение функции, если аргумент равен – 2. 4. Что является графиком прямой пропорциональности? 5. Дана функция у=2-7х, чему равно k? 6. Дана функция у=3+4х, чему равно b? 7. В каком случае графики двух линейных функции пересекаются? Вариант 2 1. Формулой какого вида задается прямая пропорциональность? 2. Что является графиком линейной функции? 3. Функция задана формулой у=5-2х, найдите значение функции, если аргумент равен 4. 4. Как расположен график функции y=kx, если k>0. 5. Дана функция у=-3-10х, чему равно b? 6. Дана функция у=8-х, чему равно k? 7. В каком случае графики двух линейных функций параллельны? Ответы
Словарный диктант Тема «Функции» Запишите математические термины:
Тема «Степень с натуральным показателем» Вариант 1 1. Как называется выражение 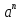 ? ?2. Как называется n в записи 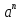 ? ?3. Представьте в виде произведения: 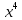 . .4. Чему равно 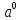 5. Каким числом является степень положительного числа? 6. каким числом является степень отрицательного числа с нечетным показателем? 7. Запишите с помощью букв правило умножения степеней с одинаковыми основаниями. 8. Запишите с помощью букв правило возведения степени в степень. 9. Запишите в виде степени: 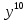 : : 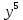 10. Запишите в виде произведения: 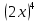 . .Вариант 2 1. Как называется а в записи 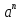 ? ?2. Запишите короче : aaaaaa=… 3. Как называется действие возведение в степень? 4. Какой показатель у a? 5. Каким числом является степень отрицательного числа с четным показателем? 6. Сравните с нулем квадрат произвольного числа. 7. Запишите с помощью букв правило деления степеней с одинаковыми показателями. 8. Запишите с помощью букв правило возведения в степень произведение двух множителей. 9. Запишите в виде степени : 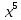 * *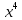 *х. *х.10. Запишите в виде степени: ( 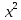 )³. )³.Ответы
Тема «Одночлены» Вариант 1 1. Приведите пример одночлена стандартного вида второй степени. 2. Запишите определение степени одночлена. 3. Запишите данный одночлен 6 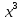 х в стандартном виде. х в стандартном виде.4. Запишите коэффициент одночлена -4х. 5. Какова степень одночлена 2 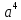 b. b.6. Представьте одночлен 0,09 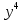 в виде квадрата. в виде квадрата.7. Какой одночлен надо возвести в куб, чтобы получить одночлен 125 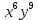 . .Вариант 2 1. Приведите пример одночлена стандартного вида первой степени. 2. Какую степень имеет одночлен, не содержащий переменных? 3. Запишите данный одночлен 2у*3х в стандартном виде. 4. Какова степень одночлена 5 abc ? 5. Запишите коэффициент одночлена ху. 6. Представьте одночлен 27 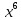 в виде куба. в виде куба.7. Какой одночлен надо возвести в квадрат, чтобы получить одночлен 10000 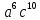 . .Ответы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

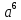
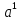
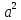 >0
>0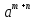
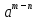 , где m>n
, где m>n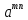
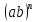 =
=