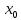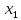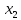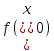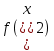Гареева В.И. 202С-21. Учебноисследовательская работа тема работы Интерполяция аналоговых сигналов Гареева В. И. студент гр. М40202С21
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА Тема работы: «Интерполяция аналоговых сигналов» Выполнил: Гареева В.И. студент гр.М40-202С-21 Консультировал: Лиханский В.И. Москва 2023 СодержаниеВведение 3 Алгебраическая интерполяция 5 Простейшие способы интерполяции 5 Интерполяционные полиномы 6 Интерполяционный многочлен Лагранжа 7 Случай равномерного распределения узлов интерполяции 8 Интерполяционный ряд Котельникова 10 Вывод 11 Список литературы 12 ВведениеБазовой теоретической моделью при цифровой обработке сигналов являются сигналы с ограниченным спектром, поскольку именно для таких сигналов дискретизация и восстановление потенциально могут быть выполнены точно. Процедура восстановления сигнала с ограниченным спектром определяется рядом Котельникова. Однако практическая реализация этой процедуры затруднена, поскольку, из-за неограниченности во времени функций Котельникова, для определения любого значения 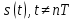 , требуется располагать всеми отсчётами сигнала , требуется располагать всеми отсчётами сигнала 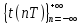 и выполнить бесконечно большое количество операций умножения и сложения. Это обуславливает поиск приближённых решений задачи восстановления сигналов, предполагающих простую физическую реализацию. и выполнить бесконечно большое количество операций умножения и сложения. Это обуславливает поиск приближённых решений задачи восстановления сигналов, предполагающих простую физическую реализацию.Восстановление аналоговых сигналов в математическом плане сводится к задаче интерполяции, то есть нахождения такой функции 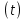 , называемой интерполирующей, которая в моменты дискретизации , , называемой интерполирующей, которая в моменты дискретизации , 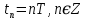 принимает значения, совпадающие с значениями сигнала, а в остальные моменты времени описывает восстанавливаемый сигнал с той или иной степенью точности. Решение задачи интерполяции неоднозначно. Классификация методов интерполяции представлена на рис.1. принимает значения, совпадающие с значениями сигнала, а в остальные моменты времени описывает восстанавливаемый сигнал с той или иной степенью точности. Решение задачи интерполяции неоднозначно. Классификация методов интерполяции представлена на рис.1.Интерполяция на основе ряда Котельникова является линейной, глобальной, регулярной и изотропной. Перечисленные признаки желательно сохранить и при поиске приближённых решений задачи интерполяции, полагая, что они обусловлены неотъемлемыми свойствами сигналов с ограниченным спектром. Однако только глобальность интерполяции рядом Котельникова обуславливает принципиальные трудности при физической реализации. Поэтому приближённые решения задачи восстановления сигналов обычно рассматривают в классе линейных, локальных, регулярных и изотропных методов. При переходе к приближённому решению задачи восстановления сигнала с ограниченным спектром, единственность решения понимается асимптотически и выражается наложением условия сходимости интерполяционного процесса, которое гарантирует, что рано или поздно увеличение информации о восстанавливаемом сигнале приведёт к его более точному восстановлению. Требуемая точность восстановления сигнала, при выполнении условия сходимости, может быть достигнута предварительным выбором периода дискретизации.  Рис.1. Классификация методов интерполяции. Алгебраическая интерполяцияТабличное задание функции: При алгебраической интерполяции для представления информации о функции f(x) используется таблица значений этой функции:
Для интерполирования функций с большим числом узлов, применяют локальную интерполяцию. Для этого заданную сетку делят на несколько интервалов с небольшим числом узлов и на каждом из интервалов строят свой интерполяционный полином, поэтому локальную интерполяцию еще называют кусочно-полиномиальной. Простейшие способы интерполяцииПростейшим способом интерполяции функции f по таблице является ступенчатая интерполяция. Один из ее вариантов формулируется так: 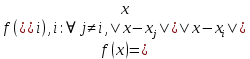 То есть за значение функции берется значение функции f(x) в точке, ближайшей к рассматриваемой. Более точным способом интерполяции является кусочно-линейная интерполяция. При таком подходе значение f(x) интерполируется по двум соседним с точкой x точкам: 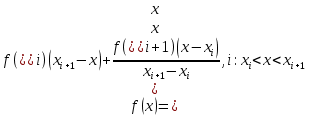 (здесь подразумевается монотонное возрастание последовательности 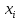 ) Интересно понять, с какой точностью интерполяционные формулы аппроксимируют функцию ) Интересно понять, с какой точностью интерполяционные формулы аппроксимируют функцию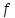 . Предположим, что производная функции . Предположим, что производная функции 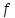 ограничена величиной ограничена величиной 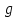 . Тогда на отрезке . Тогда на отрезке 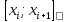 функция функция 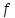 не может отклониться от линейной интер не может отклониться от линейной интер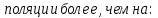 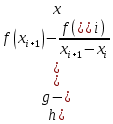 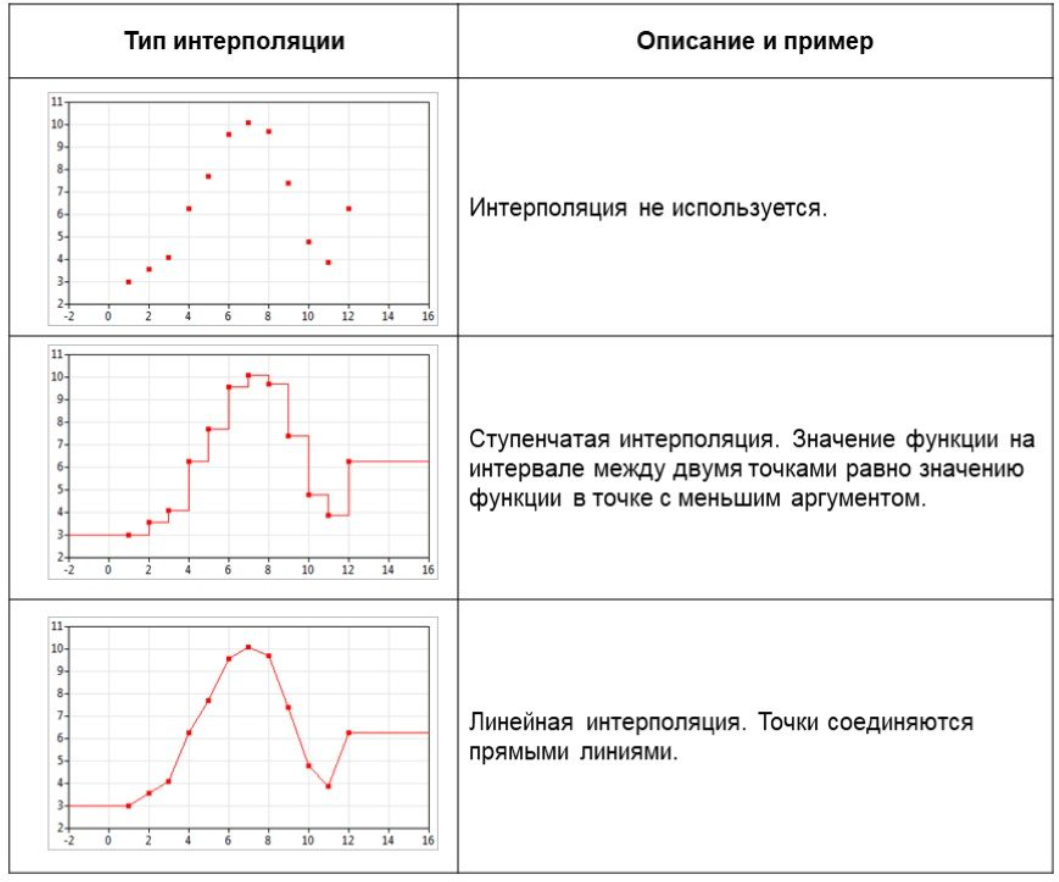 Рис.2. Тип и описание методов интерполяции. Интерполяционные полиномыАлгебраическим интерполяционным многочленом 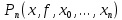 называется многочлен называется многочлен 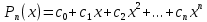 степени не выше степени не выше 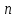 , принимающий в точках , принимающий в точках 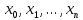 значения значения 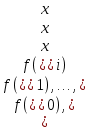 Интерполяционный многочлен ЛагранжаРассматриваемый метод интерполяции не является регулярным, однако мы обратим на него внимание, поскольку на нём основаны подходы к построению локальных регулярных методов. Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел (x0;y0), (x1;y1), …, (xn;yn), где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi. В простейшем случае (n=1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки. Лагранж предложил способ вычисления таких многочленов: 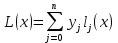 , где базисные полиномы определяются по формуле: , где базисные полиномы определяются по формуле: 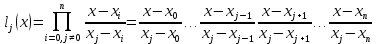 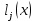 обладают следующими свойствами: обладают следующими свойствами: являются многочленами степени n 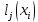 = 1 = 1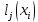 = 0 при i = 0 при i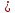 j j Отсюда следует, что L(x), как линейная комбинация lj(x), может иметь степень не больше n, и L(xj) = yj. Пусть для функции f(x) известны значения yj = f(xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как: 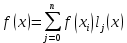 В частности, 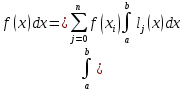 Значения интегралов от lj не зависят от f(x), и их можно вычислить заранее, зная последовательность xi. Случай равномерного распределения узлов интерполяцииВ случае равномерного распределения узлов интерполяции xi выражаются через расстояние между узлами интерполяции h и начальную точку x0: 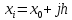 и, следовательно,  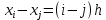 Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим 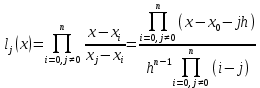 Теперь можно ввести замену переменной 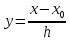 и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики. и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.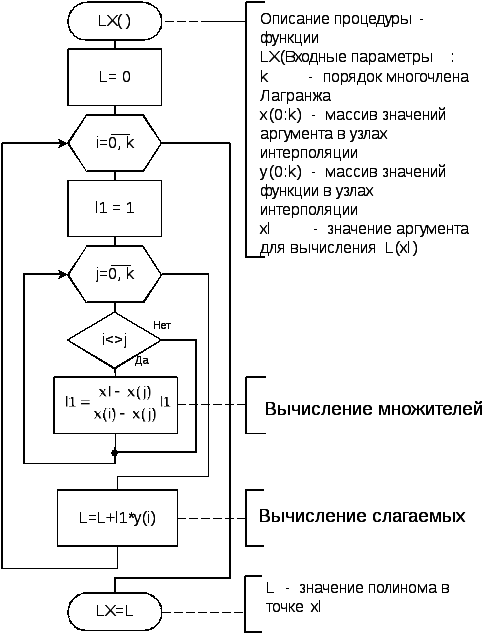 Рис.3. Алгоритм вычисления многочлена Лагранжа. . Интерполяция многочленом Лагранжа даёт приемлемые результаты на всём интервале интерполяции при n 8 . При большем числе узлов интерполяции поведение интерполирующей функции в некоторой области вблизи левой и правой границ интервала интерполяции становится геометрически непредсказуемым: часто имеет место сильная «раскачка» графика интерполирующей функции между узлами интерполяции. При этом внутри интервала интерполяции (вблизи его середины) интерполирующая функция вполне сохраняет геометрическую предсказуемость. При неограниченном увеличении количества узлов интерполяции N интерполирующая функция на основе многочлена Лагранжа асимптотически переходит в интерполирующую функцию на основе ряда Котельникова. 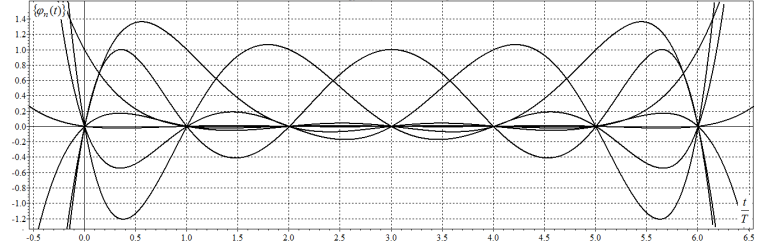 Рис.4. Базисные функции многочлена Лагранжа при n 7. 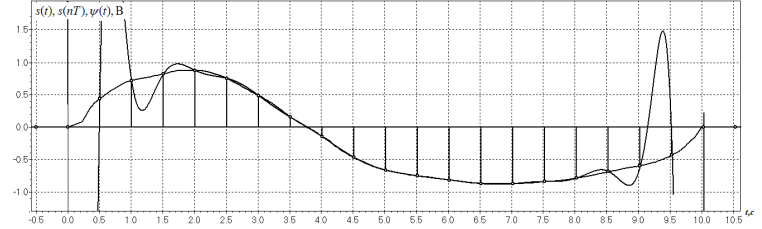 Рис.5. Пример интерполяции многочленом Лагранжа при n 21. Интерполяционный ряд КотельниковаУмножение непрерывного и бесконечного спектра на Π{\displaystyle \Pi \,\!}-импульс в пределах главного диапазона отобразится в динамической области сверткой двух функций: F⋅s(f)=F⋅S(f)⊗sinc(πFt){\displaystyle F \cdot s (f) = F \cdot S(f) \otimes sinc (\pi F t) \,\!} s(t)=sinc(πFt)⊗∞∑k=−∞s(kΔt)δ(t−kΔt){\displaystyle s (t) = sinc (\pi F t) \otimes \sum_{k = - \infty}^{\infty} s (k \Delta t) \delta (t - k \Delta t) \,\!} Отсюда, с учетом равенства δ(t−kΔt)⊗sinc(πFt)=sinc[πF(t−kΔt)]{\displaystyle \delta (t - k \Delta t) \otimes sinc (\pi F t) = sinc [\pi F (t - k \Delta t)] \,\!}, получаем: s(t)=∞∑k=−∞s(kΔt)sinc[πF(t−kΔt)](4.6){\displaystyle s (t) = \sum_{k = - \infty}^{\infty} s (k \Delta t) sinc [\pi F (t - k \Delta t)] \qquad {\color{Maroon}(4.6)} \,\!} Эта формула носит название интерполяционного ряда Котельникова и, по существу, является разложением сигнала по системе ортогональных функций sinc[πF(t−kΔt)]=sinc[π(t/Δt−k)]{\displaystyle sinc [\pi F (t - k \Delta t)] = sinc [\pi (t / \Delta t - k)]\,\!}. С другой стороны, эта формула представляет собой свертку дискретной функции данных s(kΔt){\displaystyle s( k \Delta t) \,\!} с непрерывной функцией интегрального синуса. Для больших массивов дискретных данных точность восстановления сигнала обычно ограничивается интервалом задания функции интегрального синуса, по которому устанавливается интервал суммирования. 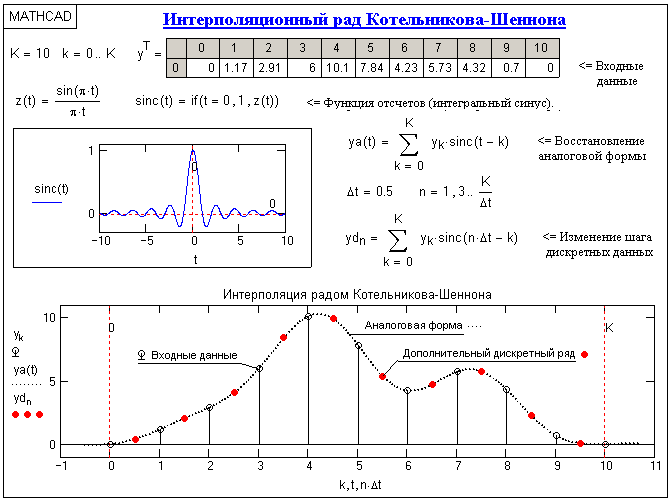 ВыводНедостатки интерполяции: В случае локальной интерполяции получается несколько интерполирующих функций, с которыми неудобно работать. В случае глобальной интерполяции при достаточно большом количестве пар точек получается достаточно сложная интерполирующая функция. Если исходная таблично заданная функция содержит в себе погрешность, то интерполирующая функция также будет «копировать» эту погрешность и не даст необходимого достоверного результата. Достоинства интерполяции: Если исходная таблично заданная функция не содержит в себе погрешность, то метод интерполяции дает достаточно точные и достоверные результаты. Список литературыВ.Н. Исаков «Радиотехнические цепи и сигналы» А.В. Пантелеев, Т.А. Летова «Прикладная математика для ВТУЗов: методы оптимизации в примерах и задачах» Макс Ж. Методы и техника обработки сигналов при физических измерениях Иванов Д.В. и др. Алгоритмические основы растровой графики |