математическое моделирование. 71_задания. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 324.07 Kb. Скачать 324.07 Kb.
|
Задание 1.Используя заданную функцию f(x), которая выбирается из таблицы № 1 по числу N10, рассчитать 5 точек в интервале [а, b/4], которые использовать как узлы интерполяции. Выбрать точку х внутри этого интервала, в которой восстановить значение функции с помощью заданного метода интерполяции. Метод интерполяции выбрать по числу N4+1 из следующего общего списка методов интерполяции:
Метод сплайнов f(x) = x+10sin(x+1)
решение будем искать в виде полинома третьей степени: Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6 Неизвестные коэффициенты ai, bi, ci, di, i=1, 2,..., N, находим из: • условий интерполяции: Si(xi)=fi, i=1, 2,..., N; S1(x0)=f0, • непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,..., N, • непрерывности первой и второй производной: S/i(xi–1)=S/i–1(xi–1), S//i(xi–1)=S//i–1(x i–1), i=2, 3,..., N. Учитывая, что для определения 4N неизвестных получаем систему 4N–2 уравнений: ai=fi, i=1, 2,..., N, bi hi – cihi2/2 + di hi3/6=fi – fi–1, i=1, 2,..., N, bi – bi–1 = ci hi – di hi2/2, i=2, 3,..., N, di hi = ci – ci–1 , i=2, 3,..., N. где hi=xi – xi–1. Недостающие два уравнения выводятся из дополнительных условий: S//(a) = S//(b)=0. Можно показать, что при этом c0=cN = 0. Из системы можно исключить неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов ci: c0 =0, cN =0, hici–1+2(hi+hi+1)ci+h i+1ci+1=6* 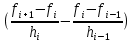 , i=1, 2,…, N–1. (1) , i=1, 2,…, N–1. (1)После этого вычисляются коэффициенты bi, di: 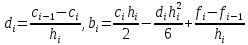 , i = 1,2…N , i = 1,2…NВ случае постоянной сетки hi=h эта система уравнений упрощается. 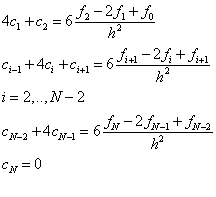 Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки. Коэффициенты bi, di определяются из формул: 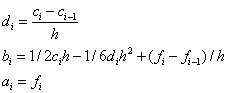 Для вычисления значения S(x) в произвольной точке отрезка z∈[a, b] необходимо решить систему уравнений на коэффициенты ci, i=1,2,…, N–1, затем найти все коэффициенты bi, di. Далее, необходимо определить, на какой интервал [xi0, xi0–1] попадает эта точка, и, зная номер i0, вычислить значение сплайна и его производных в точке z S(z)=ai0 +bi0(z–xi0)+ci0(z–xi0)2/2+di0(z–x i0)3/6 S /(z)=bi0+ci0(z–xi0)+di0(z–x i0)2/2, S //(z)=ci0+di0(z–x i0). В нашем случае: hi = 0,3125, f0 = -14,1212 f1 = -16,4103 f2 = -18,0481 f3 = -18,8459 f4 = -18,696 N = 4 Выпишем систему уравнений для определения ci: 4c1+c2 = 6(f2-2f1+f0)/h^2 = 40,01 c1+4c2+c3 = 6(f1-2f2+f3)/h^2 = 51,62 c2+4c3 = 6(f2-2f1+f0)/h^2 = 58,22 cN = 0 Решая эту систему линейных уравнений, получим: c1 = 8,0696 c2 = 7,731 c3 = 12,6233 c4 = 0 d1 = (c1-c0)/-h = -25,8227 d2 = (c2-c1/h = -1,08372 d3 = (c3-c2)/h = 15,66 d4 = (c4-c3)/h = -40,3946 b1 = ½*c1h-1/6*d1*h^2+(f1-f0)/h = -5,64 b2 = ½*c2h-1/6*d2*h^2+(f2-f1)/h = -4,02 b3 = ½*c3h-1/6*d3**h^2+(f3-f2)/h = -0,835 b4 = ½*c4h-1/6*d4*h^2+(f4-f3)/h = 1,1371 a1 = -14,1212, a2 = -16,4103, a3 = -18,0481, a4 = -18,8459 Рассмотрим точку -9.7, которая принадлежит первому отрезку, т.е. i=1. S(z) = a1+b1*(z-x0)+1/2*c1*(z-x0)^2+1/6*d1*(z-x0)^3 S(-9) = -14,1212-5,64*(-9,7-(-10))+1/2*8,0696*(-9,7-(-10))^2+1/6*-25,8227*(-9,7-(-10))^3 = -15,566 f(-9.7) = -16,329 Значения практически совпали, расхождения – ошибки округления 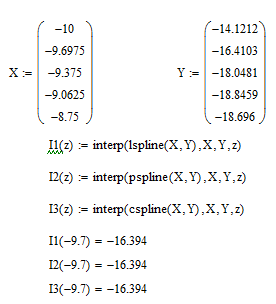 | |||||||||||||||||||||||||||||||||
