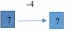
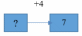
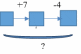
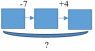
матем. мат.. Задание (Максимальное количество баллов 3 балла) Заполните позицию Необходимо определить

• Название: Задание (Максимальное количество баллов 3 балла) Заполните позицию Необходимо определить
• Анкор: матем
• Дата: 16.05.2023
• Размер: 1.13 Mb.
• Имя файла: мат..docx
• Тип: Задача; #1136571

 Задание 1. (Максимальное количество баллов – 3 балла)

Заполните позицию «Необходимо определить» в графе «Интерпретация модели» таблицы «Виды моделирования при решении текстовых задач».

Таблица – «Виды моделирования при решении текстовых задач»

Задача	Модель	Интерпретация модели
1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось?		Пример ответа: Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта. Необходимо определить числовое значение величины конечного состояния объекта.
2. Было 4 кубика, стало 6 кубиков. Что произошло?		Известно: начальное и конечное состояние объекта; направленность отношения между ними. Необходимо определить направленность отношений между начальным и конечным состоянием объекта
3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления?		Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определить  числовое значение величины начального объекта
4.Было 7 кубиков, стало 4 кубика. Что произошло?		Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта. Необходимо определить  числовое значение величины между состояниями объекта
5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате?		Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Необходимо определить  числовое значение величины между состояниями объекта
6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате?		Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить числовое значение величины между состояниями объекта
7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз?		Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить  числовое значение величины между состояниями объекта
8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз?		Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта. Необходимо определить ...

 

Задание 2. (Максимальное количество баллов – 3 балла)

 

Решите задачу, используя диаграммы Эйлера-Венна.

При выборе кружков для детей оказалось, что 60 % родителей желают, чтобы их ребенок посещал кружок рисования, 50 % предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30 % родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике,  20 %  сделали выбор в пользу занятий по гимнастике и музыке,  а 40 % родителей пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10 % из них высказались за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:

1) не желают водить детей в кружки;

2) выбрали не менее двух кружков.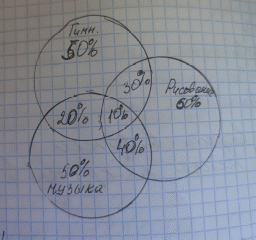

 

Решение:

1. 
   100%-(20+10+30+10++10)=20% (не желают водить детей в кружки)
   
2. 
   20+10+30+10=70%(выбрали не менее 2-х кружков)
   

Задание 3 (максимальное количество баллов – 5 баллов)

 

При измерении получены данные:

Номер измерения	1	2	3	4	5	6	7	8	9	10
Данные	20	20	5	10	10	15	20	5	5	20

 

Выполните задания с учетом исходных данных, подробно описывая ход решения.

а) Постройте статистический ряд распределения частот. 

б) Постройте полигон распределения.

в) Вычислите выборочную среднюю, дисперсию, моду, медиану. 

г) Постройте выборочную функцию распределения.

А) Подсчитаем объем, выборка из генеральной совокупности: n=10.

Посчитаем количество данных

xi	5	10	15	20
ni	3	2	1	4

Получим -10

Б) построить полигон распределения



В) Вычислите выборочную среднюю, дисперсию, моду, медиану. 

(5*3+10*2+15+20*4) : 10 = 13 (выборочная средняя)

(5+10+15+20):4 = 12,5 (дисперсия)

Мода=20

10:2 = 5 (медиана)

Задание 4 (максимальное количество баллов - 4 балла)

 

Решите примеры, связанные с погрешностями, подробно описывая ход решения.

a)   Округлите число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.

b)   Число 12,75  определено  с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления.

c)   Определите верные и сомнительные цифры числа 13,27 ± 0,03.

a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.

4,45575250≈4,455753

4,45575250≈4,45575

4,45575250≈4,4558

4,45575250≈4,456

4,45575250≈4,46

4,45575250≈4,5

4,45575250≈4

b) Число 12,75 определено с относительной погрешностью 0,3%. Найдите абсолютную погрешность округления.
Относительная погрешность равна:
δ=(∆х : 12,75)⋅100%=0,3%.
Найдём абсолютную погрешность:
∆х : 12,75 = 0,3% : 100%;
∆х : 12,75 =0,003;
∆х =0,003 *12,75;
∆х =0, 0383.
c) Определите верные и сомнительные цифры числа 13,27 ± 0,03.

х= 13,27 ± 0,03
0,03- граница абсолютной погрешности
Единица последнего разряда - 0,01 (сотые)

0,03 > 0,01
значит цифра 7 - сомнительная

0,03 < 0,1 -значит цифра 2 - верная

Задание 5 (максимальное количество баллов – 3 балла)

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см². Найдите площадь треугольника ABD.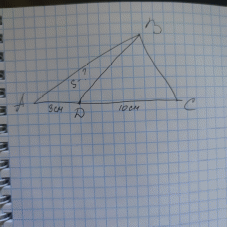

Дано: ∆АВС, AD=3см, DC=10см, SАВC = 39 см2. Найти: SАВD

Решение

ВН – общая высота треугольников.

S_АВC : S_АВD = АС : АD;

39 : S_АВD = 13 : 3;

S_АВD = 9 (см²)

Задание 6 (максимальное количество баллов – 4 балла)

 

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 150⁰.

 

Дано: ABCD – параллелограмм,
BAF = FAD,

BF=4 см,

FC=2 см,

ABC = 150°.

Найти: SАВСD

Решение
1) BAF = FAD – по условию.
BFA = FAD –АD || ВС, секущая АF.
Значит ∆ BAF – равнобедренный, и АВ = ВF = 4 см;
BFA = BAF = (180-150):2 = 15°
2) SАВСD = 1/2*АВ*ВD*sinBAD;
SАВСD =1/2* 4*6*1/2 = 6 (см2)
Ответ. 6 см2.

Задание 7 (максимальное количество баллов – 3 балла)

 

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. 

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 см и 8 см, а боковое ребро призмы равно 12 см.