математическое моделирование. 71_задания. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 324.07 Kb.
|
Задание 3.Дано уравнение f(х) = 0. Отделить корни в интервале [а, b] и уточнить один из них (любой на выбор) заданным методом. Разработать блок-схему алгоритма используемого метода. Результаты представить в виде таблиц (i - хi - f(хi)), и графиков в координатах хi - f(хi), где i – номер шага (итерации). Отделение корней произвести аналитическим или графическим методом, если аналитический метод окажется затруднительным. Уточнение корней произвести одним методом. Метод уточнения корней выбрать по числу N6+1 из общего списка методов: Метод параболической аппроксимации. В этом методе функция f(x) заменяется не линейной, а параболической функцией, что является более точной заменой. Следовательно, метод может обеспечить более быструю сходимость к решению. На первом этапе параболу обычно строят по трем точкам: крайним и средней точкам интервала (а, b), где отделен корень, т.е. (а, f(а)), ((а+b)/2, f((а +b)/2)), (b, f(b)). По полученному уравнению параболы у = с2x2+с1х+c0 находят приближенный корень (приближенный потому что парабола приближённо заменяет f(x)), для чего решают уравнение с2х2+с1х+c0=0. На втором этапе строят параболу по трём точкам: найденному приближенному корню и двум предыдущим точкам (слева и справа от этой точки), лежащим по разные стороны оси х. Такой вариант выбора точек на практике быстрее приводит к решению по сравнению с вариантом, когда для построения параболы берутся последовательно три последние точки. Эта процедура повторяется многократно до тех пор, пока величина отрезка, внутри которого находится корень, не будет меньше e – предварительно заданной погрешности. Отделим корни графически 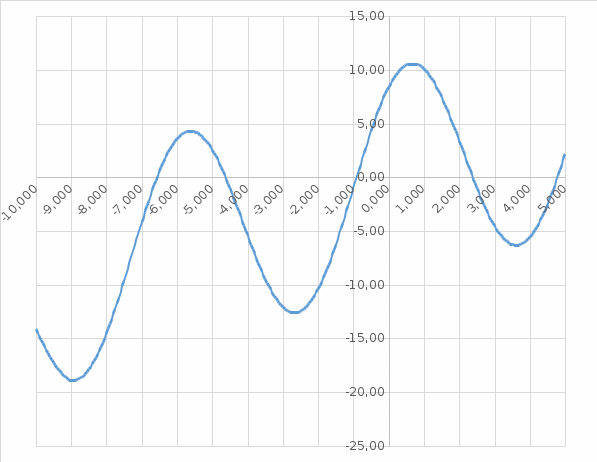 Рис. График функции f(x) = x +10*sin(x+1) на интервале [-10; 5] Блок-схема 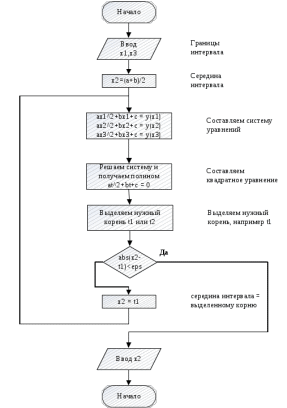 Имеем пять корней на интервале Будем искать корень, локализованный на интервале [-7;-6] Возьмем три точки -7, -6.5, -6 Запишем систему уравнений a*-7^2+b*-7+c = f(-7) a*-6.5^2+b*-6.5+c = f(-6.5) a*-6^2+b*-6+c = f(-6) Решаем ее находим a,b,c Записываем квадратное уравнение ax^2+bx+c = 0 Находим корни – это и есть первое приближение к корню уравнения. Приравниваем середину отрезка к найденному приближению и так до тех пор, пока точность не устроит. 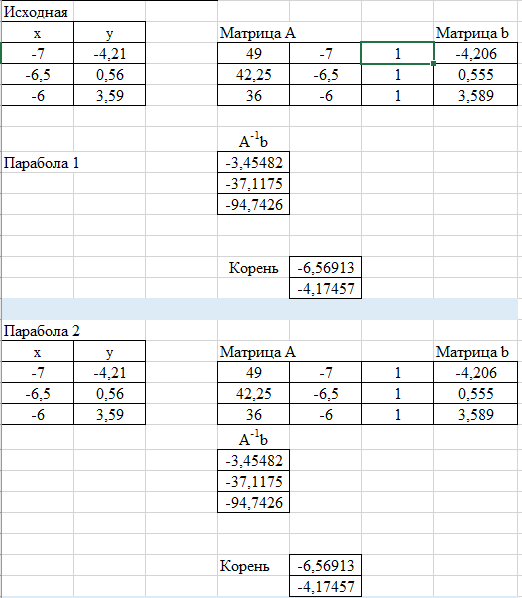 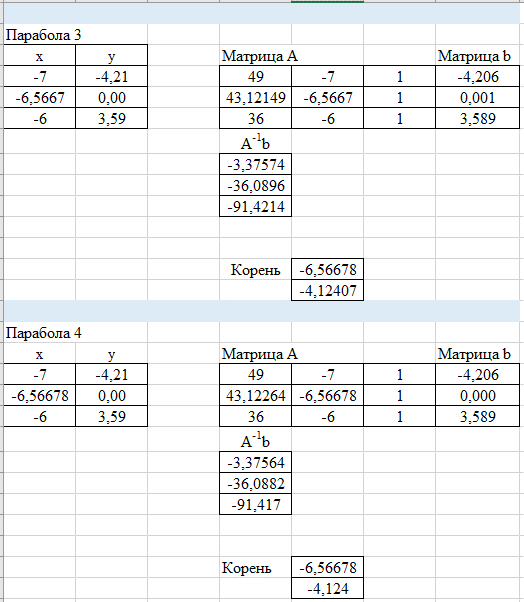 Корень = -6,56678 Проверим в MathCad 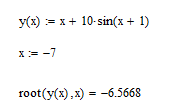 Задание 4.По заданной функции f(х) в заданном интервале рассчитать интеграл 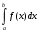 заданным методом (интервал [а, b] разбить не менее чем на шесть подынтервалов). Метод численного интегрирования выбрать по числу N4+1 из следующего общего списка методов:Методы Чебышева и Гаусса Квадратурная формула Чебышева Рассмотрим квадратурную формулу 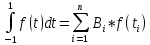 (1)где Bi - коэффициенты. Зададим коэффициенты Bi равны между собой. Абсциссы ti будем выбирать таким образом, чтобы квадратурная формула (1) являлась точной для всех полиномов до степени n включительно. Найдём Bi и ti. Полагая B1=B2= ... = n=B и учитывая, что при f(t)≡1 будем иметь 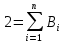 получаем B = 2/n Следовательно, квадратурная формула (1) примет вид 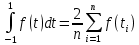 (2)Найдём теперь ti. Формула (2), согласно второму условию, должна быть точной для функций вида f(t)=t,t2,...,tn. Подставляя эти функции в (2), получим систему уравнений 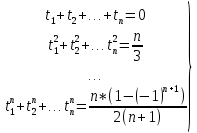 (3) из которой могут быть определены неизвестные ti, i=1,2,..,n. Формула (2), в которой абсциссы определяются системой (3), называется квадратурой Чебышева. Система (3) при n=8 и n≥10 не имеет действительных решений. В этом состоит принципиальный недостаток формулы Чебышева. Чтобы применить формулу Чебышева к интегралу вида 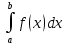 следует преобразовать его с помощью подстановки x = ½*(b+a)+(b-a)/2*t переводящей отрезок a≤x≤b в отрезок -1≤t≤1. В результате получим 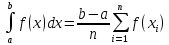 (5)xi = ½*(b+a)+(b-a)/2*ti где ti - корни системы (4). приведём значения ti для n = 6
Разобьем наш интервал на шесть подинтервалов и на каждом вычислим интеграл, используя квадратурную формулу Чебышева. Наши подинтервалы
Вычисляем x1 = (-7,5-10)/2+(-7,5+10)/2*0,866 = -7,667 y1 = -7,667+10*sin(-7,667+1) = -11,4136 x2 = (-7,5-10)/2+(-7,5+10)/2*0,423 = -8,222 y2 = -8,222+10*sin(-8,222+1) = -16,2896 x3 = (-7,5-10)/2+(-7,5+10)/2*0,266 = -8,417 y3 = -8,417+10*sin(-8,417+1) = -17,4758 x4 = (-7,5-10)/2+(-7,5+10)/2*-0,266 = -9,083 y4 = -9,083+10*sin(-9,083+1) = -18,8215 x5 = (-7,5-10)/2+(-7,5+10)/2*-0,423 = -9,28 y5 = -9,28+10*sin(-9,28+1) = -18,392 x6 = (-7,5-10)/2+(-7,5+10)/2*-0,86625 = -9,833 y6 = -9,833+10*sin(-9,833+1) = -15,413 y1+y2+y3+y4+y5+y6 = -97,8052 Интеграл на этом интервале = (-7,5+10)/6*-97,8052 = -40,7522 Далее также на каждом интервале, затем сумма интегралов даст искомый интеграл 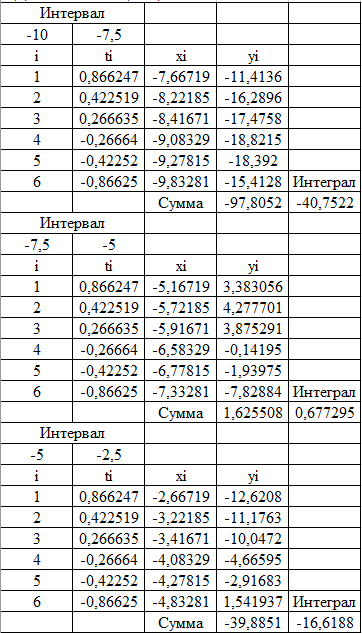 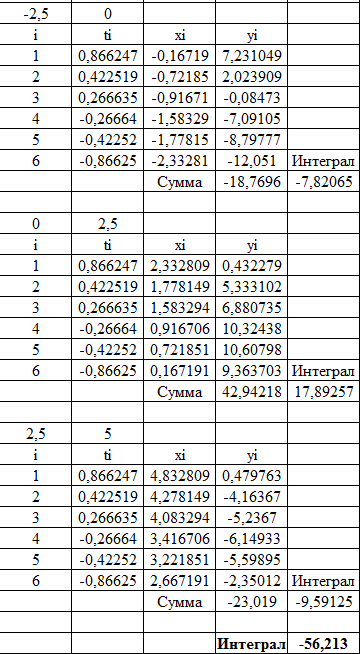 Искомый интеграл = -56,213 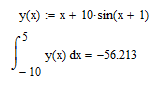 Квадратурная формула Гаусса Для произвольного интервала [a;b] формула Гаусса имеет вид 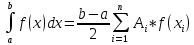 где xi = ½*(b+a)+(b-a)/2*ti ti - нули полинома Лежандра Pn(t).
Разобьем наш интервал на шесть подинтервалов и на каждом вычислим интеграл, используя квадратурную формулу Гаусса. Вычисляем x1 = (-7,5-10)/2+(-7,5+10)/2*0,93247 = -7,5844 y1 = (-7,5844+10*sin(-7,5844+1))*0,1713145 = -1,8077 x2 = (-7,5-10)/2+(-7,5+10)/2*0,661209 = -7,92349 y2 = (-7,92349+10*sin(-7,92349+1))*0,36076158 = -5,01382 Аналогично рассчитываем y3,y4,y5,y6 y1+y2+y3+y4+y5+y6 = -32,6017 Интеграл на этом интервале = (-7,5+10)/2*-32,6017 = -40,7522 Далее также на каждом интервале, затем сумма интегралов даст искомый интеграл 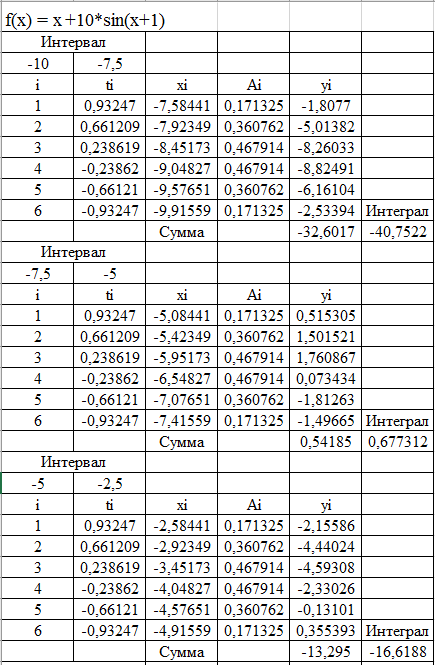 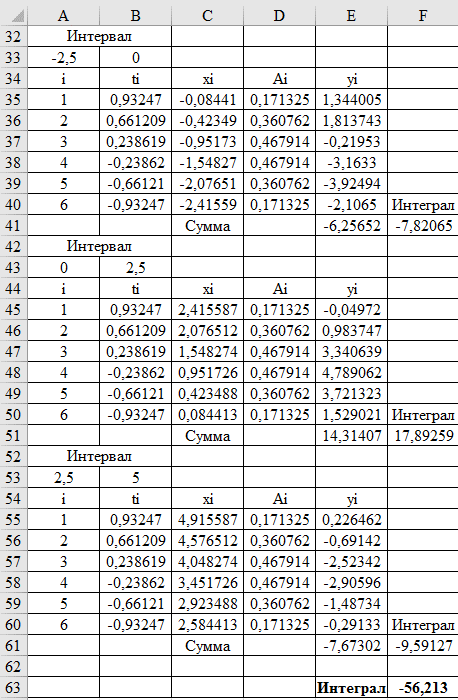 Искомый интеграл = -56,213 |