Исходные данные для расчета конечный. Исходные данные для расчета
 Скачать 172.79 Kb. Скачать 172.79 Kb.
|
|
Исходные данные для расчета 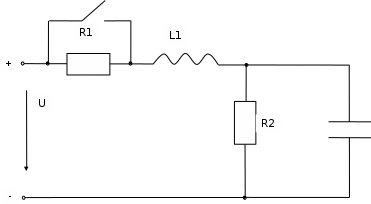 С3
Метод переменных состояния Рассмотрим начальные независимые условия 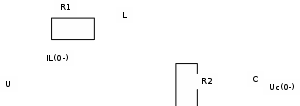 iL(0-)= 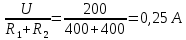 iL(0+)= iL(0-)=0,25А Uc(0-)= Uc(0+)= iL(0-)×R2=0,25×400=100В  1.Составим систему уравнений для t≥0, методом переменных состояния. Используя законы Кирхгофа получим исходную систему уравнений. 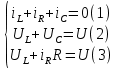 Учтем также: 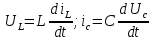 Из уравнения (2) получим: 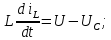 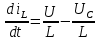 . (4) . (4)Из уравнения (1) запишем: 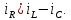 Результат подставим в уравнение (3): 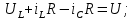 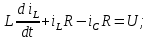 произведем замену 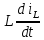 и и 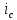 , а также сократим на U. , а также сократим на U.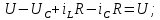 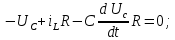 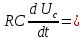 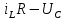 ; ; 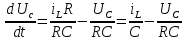 . (5) . (5)Система дифференциальных уравнений и ее решение произведем в программе Mathcad: 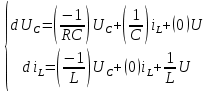 (I) (I)А= 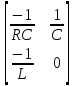 В= В=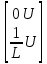 V=U V=UОпределение собственных чисел: 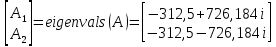 p1 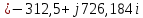 p2 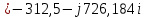 Продолжим решение аналитически. При t→∞ определим принужденные составляющие. В установившемся режиме уравнение примет вид: 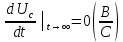 ; ;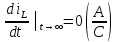 . .Тогда уравнения (4) и (5) примут вид 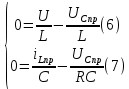 Решим систему относительно 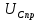 и iLпр и iLпр Из уравнения (6) получим 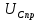 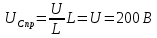 ; ; Тогда из уравнения (7) : 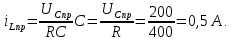 Корни характеристического уравнения найдем, приравняв к нулю определитель характеристической матрицы p1 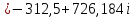 p2 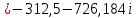 α=-312,5(с-1) ωсв=726,184 ( 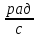 ) )С помощью законов коммутации определим независимые начальные условия iL(0)= 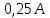 ; Uc(0)=100В. ; Uc(0)=100В.Подставим эти значения в систему (I) и получим: 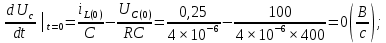 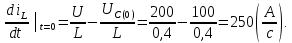 Для определения постоянных интегрирования составим систему уравнений. 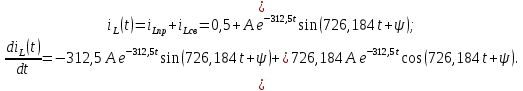 При t=0 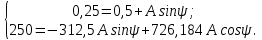 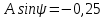 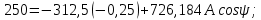 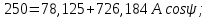 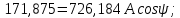 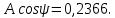 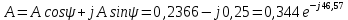 . .Отсюда А=0,344 ; 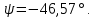 Окончательный результат 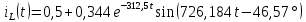 А. А.Рассчитаем напряжение на катушке. 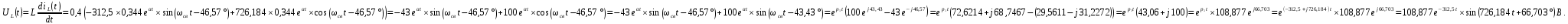 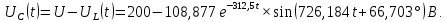 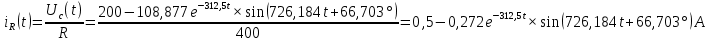 . .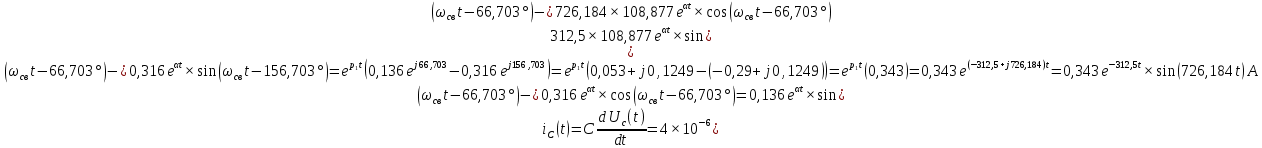 . .Операторный метод 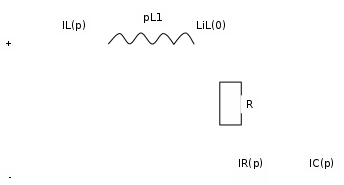 Операторная схема замещения исходной электрической цепи рис . Определим независимые начальные условия: iL(0)=0,25 А; 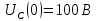 . .Составим систему уравнений по закону Кирхгофа: 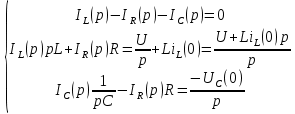 Запишем в матричной форме. 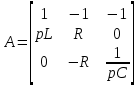 b= b= 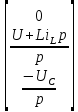 A1= 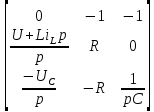 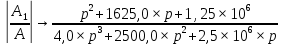 Изображение тока индуктивности: 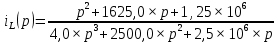 Корни уравнения найдены: 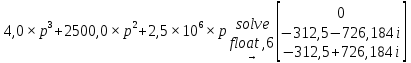 p0=0 p1= 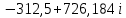 p2= 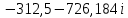 Найдем оригинал тока индуктивности: 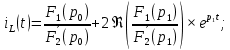 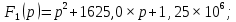 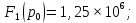 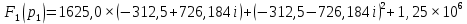 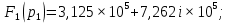 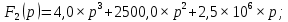 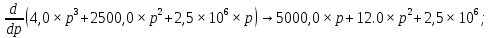 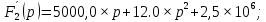 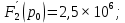 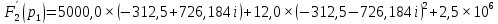 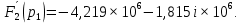 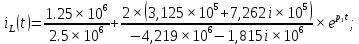 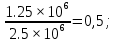 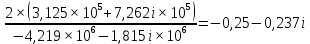 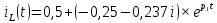 W= 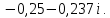 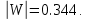 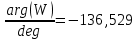 . .Графики переходных процессов: 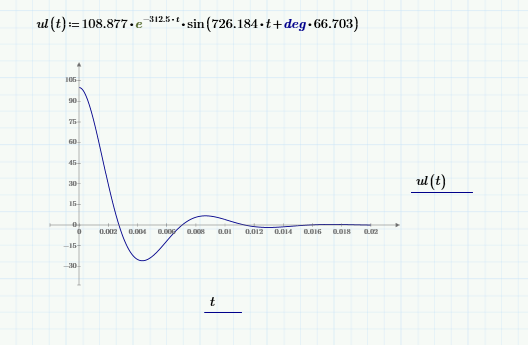 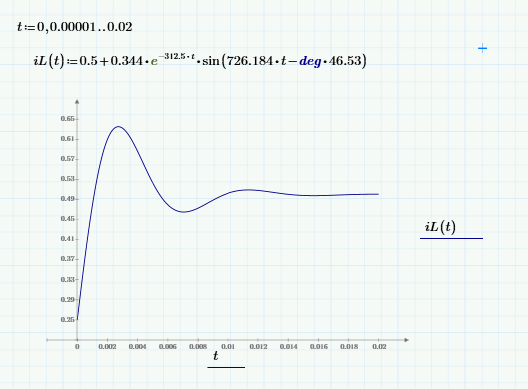 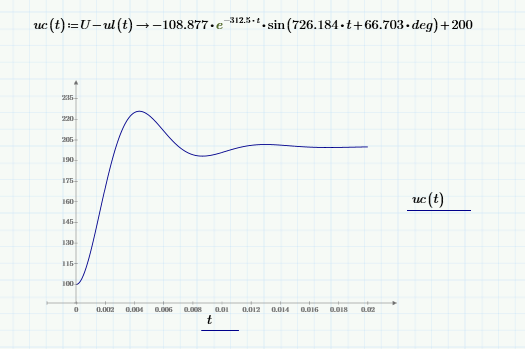 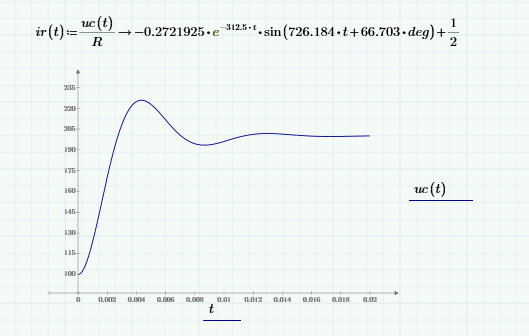 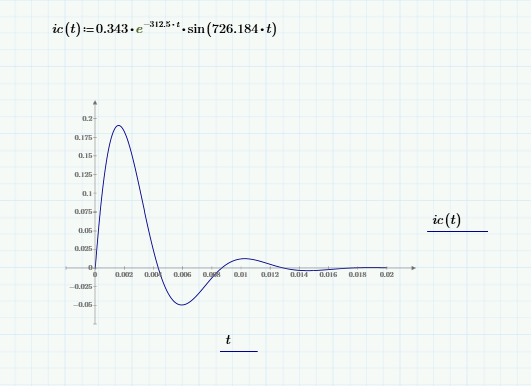 Закон изменения тока индуктивности запишем: 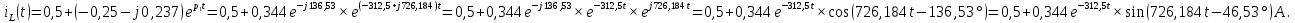 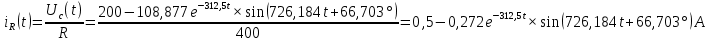 . .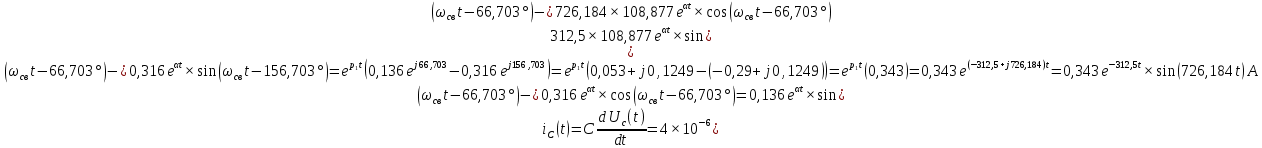 . .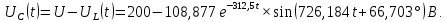 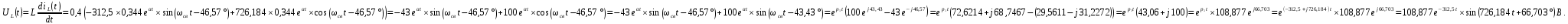 |
