Расчёт, механика. Учебнометодические указания и контрольные задания для студентов мгри москва 2020 Составители Г. В. Лукошков, В. А. Барашков, С. Ю. Некоз
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
 МинОБРНАУКИ РОСССИИ ФГБОУ ВО «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ имени Серго Орджоникидзе» (МГРИ) Кафедра механики И ИНЖЕНЕРНОЙ ГРАФИКИ Равновесие системы тел под действием плоской произвольной системы сил с учетом сил трения (скольжения) Учебно-методические указания и контрольные задания для студентов МГРИ Москва 2020 Составители: Г.В. Лукошков, В.А. Барашков, С.Ю. Некоз Равновесие системы тел под действием плоской произвольной системы сил с учетом сил трения (скольжения) В работе даны основные положения, определяющие равновесие системы тел с учетом силы трения, приведены варианты заданий и пример расчета. Российский государственный геологоразведочный университет 2020 . Введение Предлагаемое методическое пособие является руководством и пояснением к выполнению расчетно-графической работы по курсу теоретической механики (статики) для студентов МГРИ. Выполнение данной работы позволяет студентам закрепить полученные теоретические знания и практические навыки решения задач статики. 1. Основы теории Для выполнения настоящей расчетной работы необходимо изучить следующие разделы статики твердого тела: основные понятия и исходные положения (аксиомы) статики; условия равновесия плоской системы сходящихся сил; равновесие произвольной плоской системы сил; равновесие системы тел; законы трения скольжения, равновесие при наличии трения; центр тяжести твердого однородного тела. При решении задачи используются следующие основные формулы: 1) основная форма записи условия равновесия плоской произвольной системы сил в координатной форме: 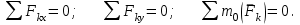 (I) (I)2) формула для определения предельной силы трения скольжения 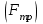 : :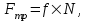 (II) (II)где: f – коэффициент трения скольжения; N – нормальная реакция опорной поверхности. 2. указания и рекомендации по выполнению и оформлению работы Прежде чем приступить к выполнению работы, следует изучить необходимый теоретический материал, подробно познакомиться с настоящими указаниями и уяснить смысл и порядок работы. В работе рассматривается равновесие системы тел под действием плоской системы сил при наличии сил трения скольжения. При решении подобных задач удобно использовать следующую последовательность. На первом этапе рассматривается равновесие всей системы как твердого тела, не учитывая при этом внутренние силы взаимодействия отдельных тел, из которых состоит система. Если при этом задача оказывается статически неопределимой (т.е. число неизвестных превышает число возможных уравнений статики), то дополнительно рассматриваются условия равновесия отдельных тел, уже с учетом соответствующих внутренних связей. При решении задания следует рассматривать предельное положение равновесия, когда 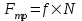 . Уравнения равновесия упростятся, если их составлять в виде уравнений моментов сил относительно точек пересечения линий действия двух и более неизвестных сил. . Уравнения равновесия упростятся, если их составлять в виде уравнений моментов сил относительно точек пересечения линий действия двух и более неизвестных сил.В данном задании обязательно проводится проверочный расчет. Студент во всех задачах выбирает номер рисунка по последней цифре шифра или номера студенческого билета, номер условия (вариант) в таблице - по предпоследней: например, если шифр оканчивается числом 52, то берутся рис.2 (т.е. схеме №2) и условия №5 из таблицы. Если номер студенческого билета однозначен (скажем, 5), то шифр принимается как 05. Оформляется работа в соответствии с принятой формой. Титульный лист выполняется на чертежной бумаге формата А4. Все надписи на титульном листе исполняются чертежным шрифтом, рамка обязательна. Содержание титульного листа приводится ниже. Текстовая часть выполняется на листах писчей бумаги стандартного формата А4, аккуратно, разборчивым почерком, без исправлений и помарок. Рисунки выполняются с помощью чертежных инструментов ручкой или карандашом с соблюдением основных правил черчения и соотношения размеров. Брошюруется работа в обязательном порядке. При выполнении работы в электронном виде, помимо распечатанной работы, представляется и электронная версия (файл). Защищается выполненная работа в индивидуальном порядке путем собеседования с преподавателем. При защите проверяется выполнение домашних задач и определяется степень усвоения студентом изученного теоретического материала. Пример выполнения работы Два однородных стержня AB и CE шарнирно соединены в точке B (рис. I, а). Конец стержня AB (А), закреплен шарнирно, а нижний конец стержня CE (E) опирается на горизонтальную шероховатую поверхность KL. На стержень AB действует пара сил с моментом m. Определить минимальный коэффициент трения между концом E стержня CE и опорной поверхностью KL при положении равновесия данной системы тел, а также реакции связей в шарнирах A и B и в точке E, если известно, что длина AB =ВE= 2∙а (м);CE= 3∙а(м); = 600, m = Р∙а(H∙м). Вес стержня длиной а равен Р(H) – см. рис. I, a. 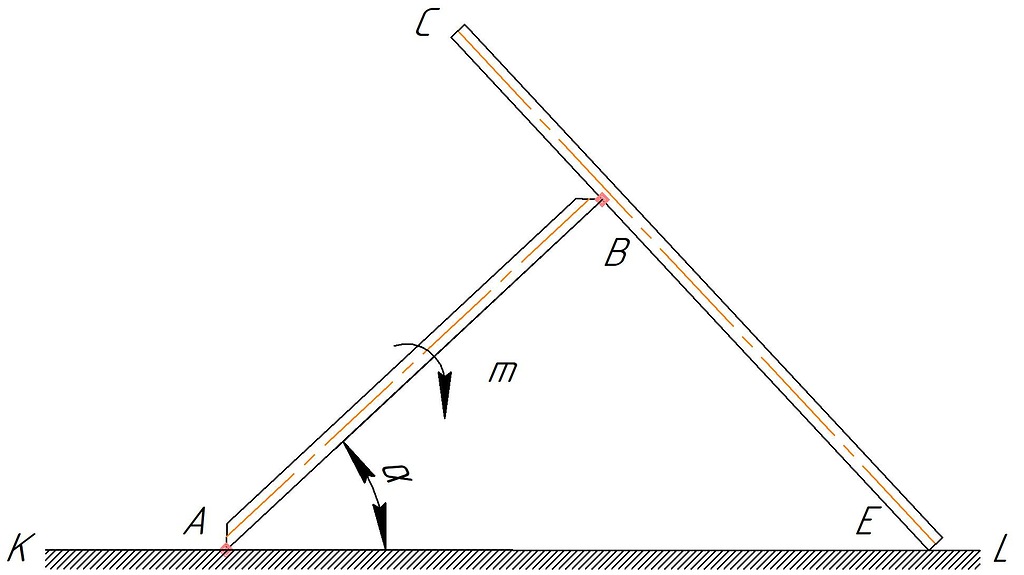 Рис. I, a Решение 1. Для рассмотрения условий равновесия данной системы тел необходимо составить расчетную схему, используя аксиому связей. Решая задачу в соответствии с этой аксиомой, мысленно отбрасываем связи и заменяем их действие силами реакций отброшенных связей. Другими словами, несвободную систему тел превращаем в свободную (рис. I, б). 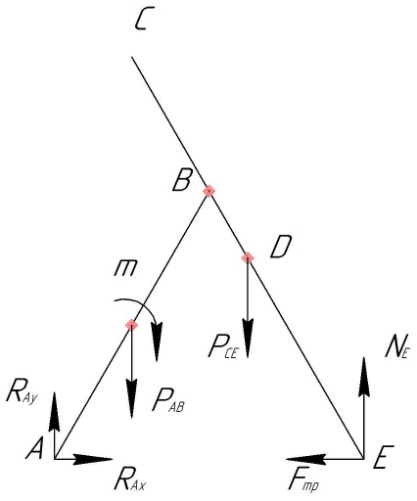 Рис. I, б 2. Исследуя составленную расчетную схему, получаем, что заданная система тел находится в равновесии под действием трех внешних активных силовых факторов (известных) и четырех реактивных сил (неизвестных). Рассматриваемая система семи силовых факторов является плоской произвольной системой сил. Условия равновесия такой системы определяются тремя уравнениями (I). 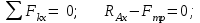 (1) (1)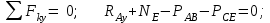 (2) (2)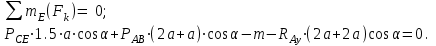 (3) (3)Таким образом, для данной расчетной схемы число неизвестных величин (4: RAx; Fтр; RAy; NE) превышает число возможных уравнений равновесия (3). Для получения дополнительных уравнений равновесия, и имея в виду, что каждое тело системы находится в равновесии, рассмотрим условия равновесия каждого тела или одного из них в отдельности. 3. На стержень АВ, если рассматривать его как отдельное свободное тело, действуют шесть силовых факторов: два внешних, активных (известных), и четыре реакции связи в шарнирах А и B. Эта расчетная схема изображена на рис. I, в. 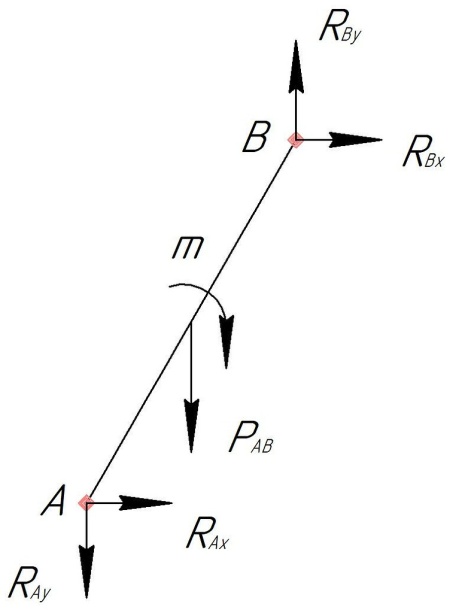 Рис. I, в Для стержня АВ, как свободного тела, условия равновесия определяются также тремя уравнениями (II): 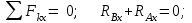 (1') (1')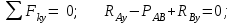 (2') (2')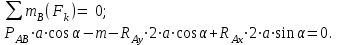 (3') (3')4. Рассматривая совместно две расчетные схемы, имеем систему из шести уравнений, определяющих условия равновесия как всей системы тел, так и отдельно стержня АВ. В эти уравнения входят шесть неизвестных, которые необходимо определить. Из уравнения (3) и расчетной схемы рис. I, б 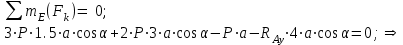 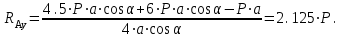 Из уравнения (2) для расчетной схемы рис. I, б 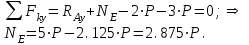 Из уравнения (3') для расчетной схемы рис. I, в 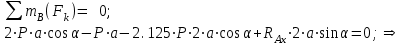 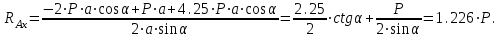 Из уравнений (1) и (1') 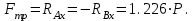 Из уравнения (II) 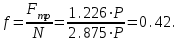 Проверка Из уравнения (3) и расчетной схемы рис. I, б 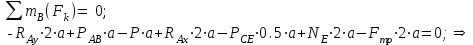 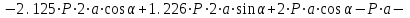 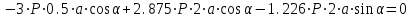 Если решение верное, то после подстановки числовых значений всех величин, как известных по условию задачи, так и определенных при ее решении, получаем: 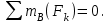 При проверке, результат может не быть равен 0. Это естественно при округлении значений. Поэтому допустимо отклонение в пределах 5% от самого большого значения. Варианты заданий Задание 0. Два однородных стержня АВ и BС соединены шарнирно в т.B (рис. 0). Длина AD=BC=2a; AB=3a. Поверхность стены (EF) шероховатая. На стержень АВ действует пара сил с моментом m. Вес стержня длиной а (м) равен Р (H). Угол α=450. Определить коэффициент трения f в точке C и реакции связей в точках A и D для следующих данных (табл. 0). Таблица 0
Задание 1. Два однородных стержня АВ и CD соединены шарниром в т. C (рис. 1). Длина AB=CD=3a; AC=2a. Поверхность стены EF – шероховатая. На часть ACстержня АВ действует равномерно распределенная нагрузка интенсивностью q. Вес стержня длиной а (м) равен Р (Н). Угол α=300. Определить коэффициент трения f в точке D и реакции связей в точках А и Bдля следующих данных (табл. 1). Таблица 1
Задание 2. Однородный стержень AB длиной 3a (рис. 2) закреплен в точке А и С шарнирно. В точке N к нему приложена сила F. AN = a; АС = CD = 2 a. Поверхность ЕК шероховатая. Вес стержня длиной а (м) равен P (H). Угол ADC – α = 600. Определить коэффициент трения f между стержнем CD и поверхностью ЕК, а также величину реакции связи в точке А для следующих данных (табл. 2). Таблица 2
Задание 3. Однородный стержень AB длиной 3a (рис. 3) опирается концом A на шероховатую поверхность EF, а в точке C соединен шарнирно со стержнем CD (AC = CD = 2 a). Вес стержня длиной а (м) равен P (H). Угол α = 450. На стержень АВ действует пара сил с моментом m. Стержень CD в точке D закреплен шарнирно. Определить коэффициент трения f между стержнем АВ и поверхностью ЕF, а также реакции связи в точке D для следующих данных (табл. 3). Таблица 3
Задание 4. Два однородных стержня АВ и ВС соединены шарнирно в точке B (рис. 4). Концом C стержень ВС опирается на шероховатую поверхность, а конец Aстержня АВ закреплен шарнирно. На участок DB стержня АВ действует равномерно распределенная нагрузка интенсивности q. Длина DB = 2a; AB = AC = 3a; α = 300. Вес стержня длиной а (м) равен Р (Н). Определить коэффициент трения f в точке С между стержнем ВС и поверхностью EF, а также реакции связи в точках А и В для следующих данных (табл. 4). Таблица 4
Задание 5. Однородный стержень CD длиной 2a концом D опирается на шероховатую поверхность, а серединой на стержень AB (рис. 5). Стержень AB жестко заделан концом A в стену MN. Угол наклона стержня CD - = 600. Трение в точке B отсутствует. Вес стержня длиной (м) равен P (H). В точке E на стержень AB действует вертикальная сила F. Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке A для следующих исходных данных (табл. 5). Таблица 5
Задание 6. Однородный стержень CD длиной 3а концом D опирается на шероховатую поверхность, а точкой Е (DE = 2a) на стержень АВ (рис. 6). Стержень АВ длиной 2а жестко заделан в стену MN концом А. Угол наклона стержня CD - α = 450. Трение в точке Е отсутствует. В середине стержня AB действует пара сил с моментом m. Вес стержня длиной а (м) равен P (H). Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке А для следующих данных (табл. 6). Таблица 6
Задание 7. Однородный стержень CD длиной 2.5а концом D опирается на шероховатую поверхность, а точкой Е (DE = 1.5 а) на стержень АВ (рис. 7). Стержень АВ длиной 2а жестко заделан в стену MN концом А. Угол наклона стержня CD - α = 450. Трение в точке Е отсутствует. На стержень АВ на участке AF = a действует равномерно распределенная нагрузка интенсивности q. Вес стержня длиной а (м) равен P (H). Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке А для следующих данных (табл. 7). Таблица 7
Задание 8. Два однородных стержня АВ и BС соединены шарнирно в т.B(рис. 8). Длина AB = 3a; AD = BC = 2a. Поверхность стены EFшероховатая. Вес стержня длиной а (м) равен Р (H). Определить коэффициент трения fв точке С и реакции связей в точках А, В и D для следующих данных (табл. 8). Таблица 8
Задание 9. Два однородных стержня АB и CD соединены шарнирно в т. C (рис. 9). Длина AB = CD = 2a; AC = a. Поверхность стены EF шероховатая. Вес стержня длиной а (м) равен Р (Н). Определить коэффициент трения fв точке Dи реакции связей в точках А, В и C для следующих данных (табл. 9). Таблица 9
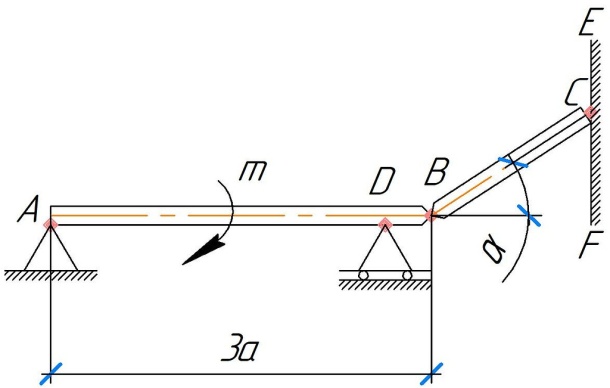 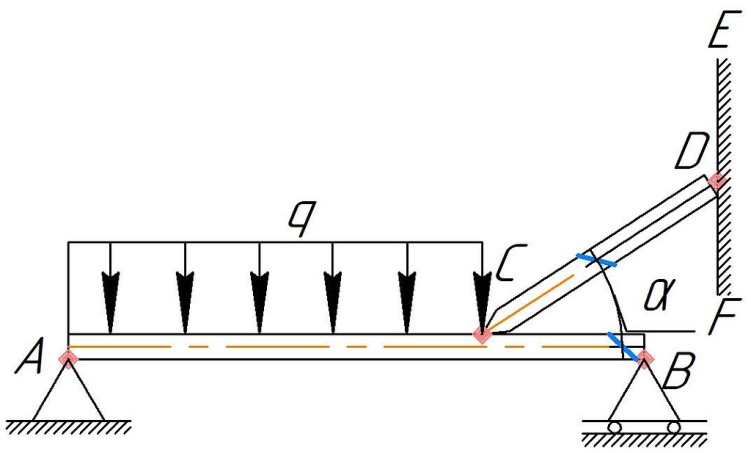 Рис. 0 Рис. 1 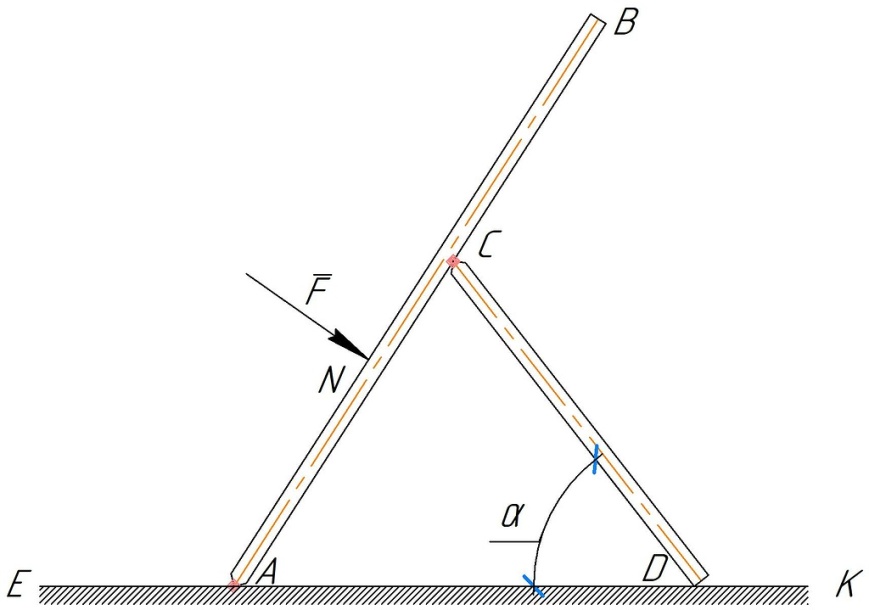 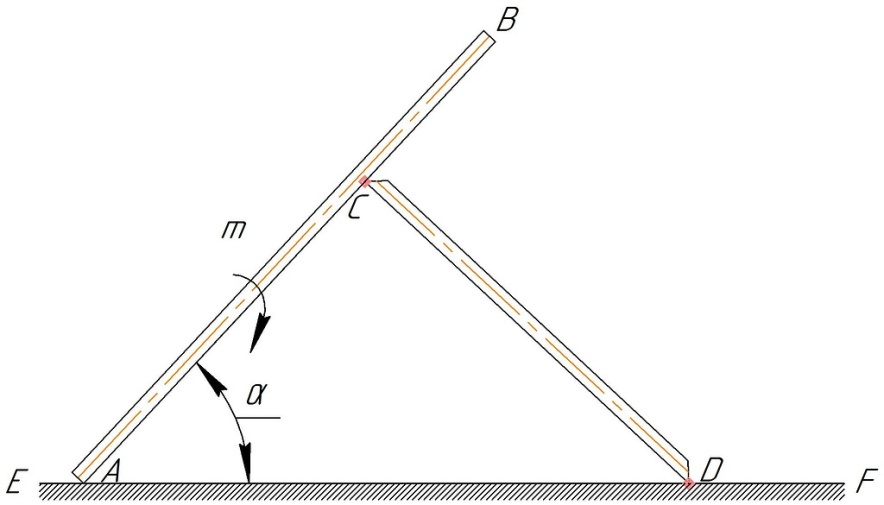 Рис. 2 Рис. 3 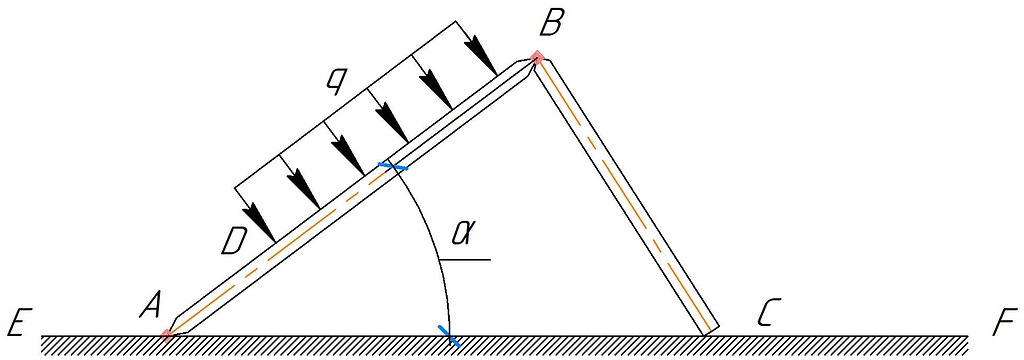 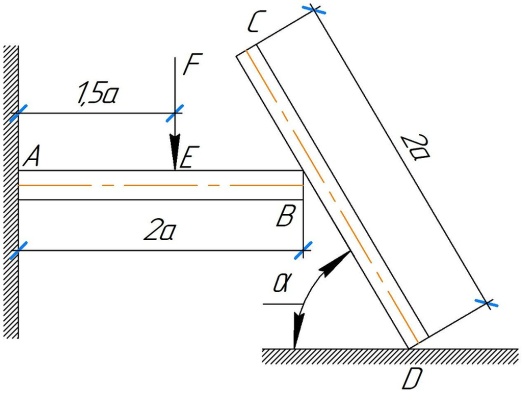 Рис. 4 Рис. 5 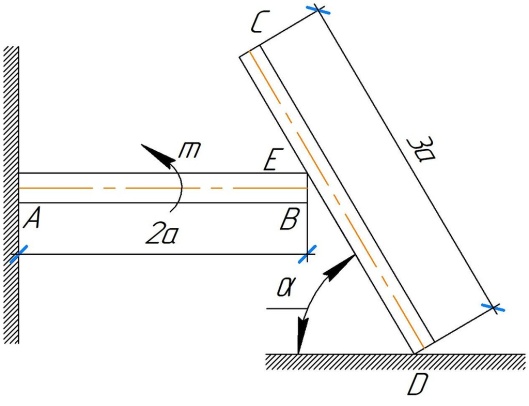 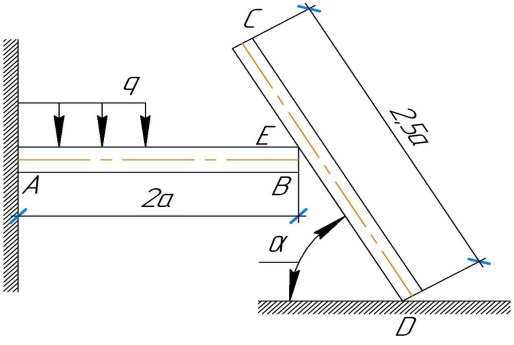 Рис. 6 Рис. 7 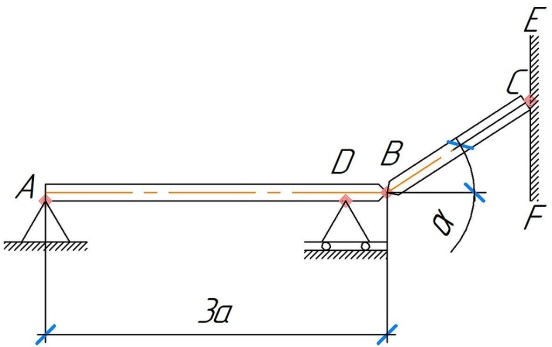 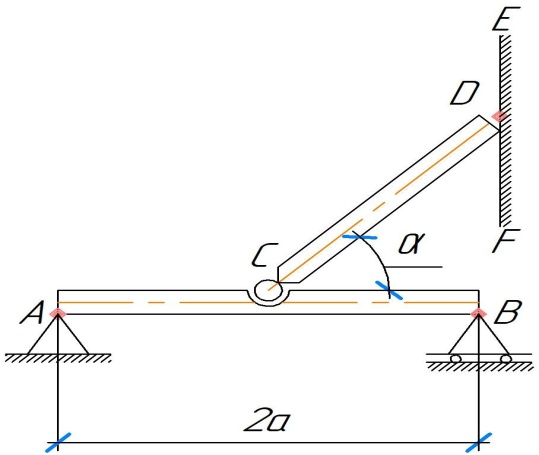 Рис. 8 Рис. 9 российский государственный геологоразведочный университет имени серго орджоникидзе (МГРИ) кафедра механики И ИНЖЕНЕРНОЙ ГРАФИКИ Расчетная работа по теоретической механике Равновесие системы тел под действием плоской произвольной системы сил с учетом сил трения (скольжения) Вариант N Выполнил: студент группы студенческий билет № ___________________ _____________ ___________________ (подпись) (ФИО) Проверил: доцент каф. Механики и инженерной графики Москва, 2020 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
