МУ к ИДЗ по физике 1 семестр специальности ИС, ПГ (1). Учебнометодическое пособие для выполнения индивидуальных домашних заданий студентами очной формы обучения по направлениям подготовки Информационные системы и технологии

• Название: Учебнометодическое пособие для выполнения индивидуальных домашних заданий студентами очной формы обучения по направлениям подготовки Информационные системы и технологии
• Дата: 23.12.2021
• Размер: 1.12 Mb.
• Имя файла: МУ к ИДЗ по физике 1 семестр специальности ИС, ПГ (1).doc
• Тип: Учебно-методическое пособие; #315560
• страница: 3 из 6

Задача 5. Круглая платформа радиуса R = 1 м, момент инерции которой J = 150 кгм², вращается по инерции вокруг вертикальной оси, делая n₁ = 1,5 об/с. На краю платформы стоит человек, масса которого m = 50 кг. Сколько оборотов в секунду n₂ будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки.

Дано: R = 1 м J = 150 кгм2 m = 50 кг

n2-?

Решение:

Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы платформа–человек выполняется закон сохранения момента импульса:

L₁= L₂. (1)

где L₁– начальный момент импульса системы (человек стоит на краю платформы), L₂– конечный момент импульса системы (человек стоит в центре платформы).

Начальный момент импульса системы равен:

(2)

где mR²– момент инерции человека, – начальный момент инерции системы, w₁ - ее начальная угловая скорость.

Конечный момент импульса системы равен:

(3)

где J₂ и w₂– конечные момент инерции и угловая скорость системы.

Приравняем правые части уравнений (2) и (3):

,

откуда

(4)

Подставив в (4) числовые значения заданных величин и выполнив вычисление, находим



Ответ: n₂ = 2,0 об/с.
Задача 6. Ракета, летевшая над поверхностью Земли на высоте h, в результате кратковременного действия мощной тормозной установки останавливается. С какой скоростью упадет ракета на Землю? Сопротивлением воздуха пренебречь.

Дано: h

v-?

Решение:

Рис.2

Из закона сохранения энергии, примененного к системе ракета–Земля, следует, что падающая ракета будет приобретать кинетическую энергию за счет убыли потенциальной энергии в поле тяготения Земли: Т = – П, (1)

где Т – кинетическая энергия ракеты у поверхности Земли; П = П₂– П₁ – изменение потенциальной энергии ракеты за время ее падения из точки 1 в точку 2 (рис. 2).

Потенциальные энергии тяготения в начальном П₁ и конечном П₂ положениях ракеты определим по формулам:

(2)

(3)

где m – масса ракеты; M – масса Земли; R – радиус Земли

Подставим (2), (3) в (1), получим:

(4)

Выразим из (4) искомую скорость:





Ответ:

Задача 7. Определить импульс и кинетическую энергию электрона, движущегося со скоростью 0,7с (где с – скорость света в вакууме).

Дано: v=0,7c

p-? T - ?

Решение:

Импульсом частицы называется произведение массы частицы на скорость ее движения:

р = тυ. (1)

Так как скорость электрона близка к скорости света, то не обходимо учесть зависимость массы от скорости, определяемую по формуле: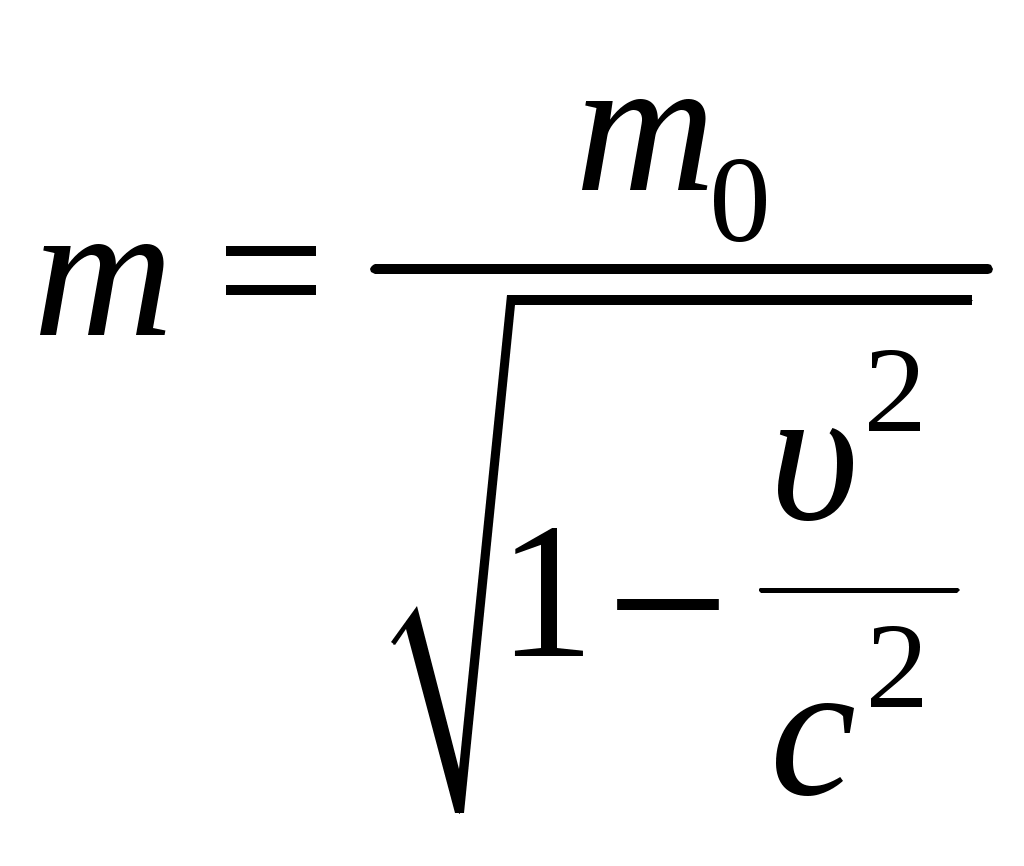

, (2)

где m – масса движущейся частицы, m₀ – масса покоящейся частицы.

Подставляя (2) в (1) получим: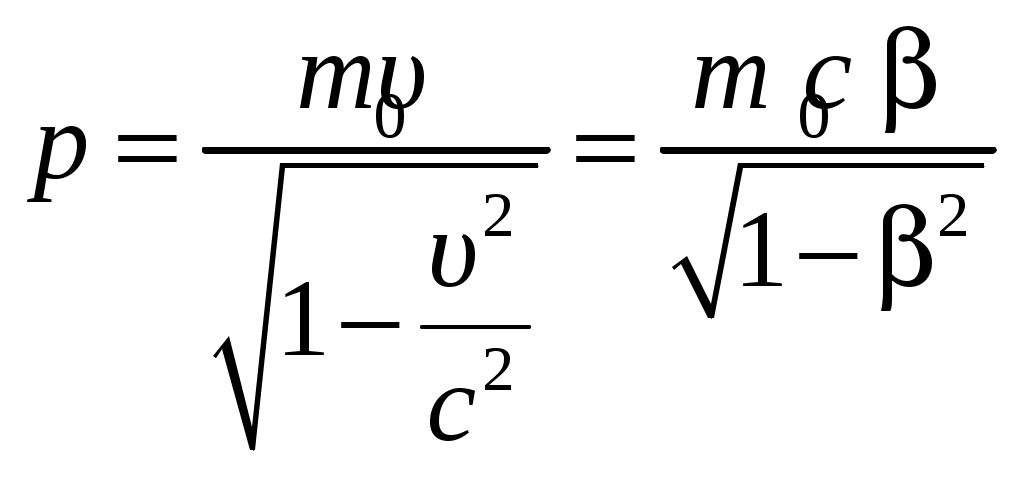

. (3)

Поскольку  = υ/с = 0,7, получим:



Кинетическая энергия T в релятивистской механике определяется как разность между полной энергией частицы 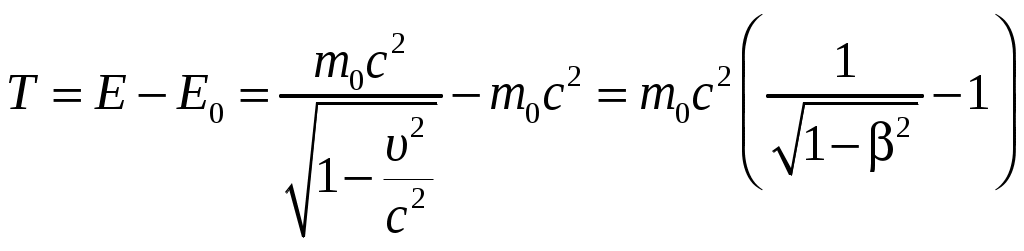и ее энергией покоя , т.е. с учетом (2):

. (4)

Найдем численное значение T, подставив числовые данные в формулу (4):



_{Ответ: р = 2,710}^-22 _{кгм/с, Т = 3,310}^-14_Дж.
Задача 8. Найти импульс mv молекулы водорода при температуре Т = 300 К. Скорость молекулы считать равной средней квадратичной скорости.

Дано:  = 0,002 кг/моль NA=6,021023 моль -1 Т = 300 К υ = <υкв>

mv - ?

Решение:

Масса молекулы водорода

(1)

где – молярная масса, для водорода  = 0,002 кг/моль; N_A– постоянная Авогадро, N_A = 6,0210²³ моль ^-1 .

Средняя квадратичная скорость молекулы равна , (2)

Импульс молекулы равен:

. (3)

.

Ответ:
Задача 9. Азот массой m = 7 г при температуре Т₁ = 290 К находится под давлением Р₁ = 0,1 МПа. Вследствие изобарного нагревания азот занял объем V₂ = 10 л. Найти: 1) объем V₁ газа до расширения; 2) температуру t₂ газа после расширения; 3) плотности газа до и после расширения.

Дано: µ=2,8·10-2кг/моль m=7·10-3кг Р1=105 Па = const T1=290 K V2 =10л Р2=Р1	СИ 10-2м3
V1-?; t2-?; ρ1-?; ρ2-?

Решение:

Найдем объем газа до расширения, используя уравнение Клапейрона- Менделеева:

, отсюда .

Записав уравнение Клапейрона-Менделеева для конечного состояния, найдем температуру Т2 : , отсюда ,

тогда t2 =T2 – 273. Плотности газа до и после расширения равны, соответственно: и .

Ответ: V1=6,02л; t2 =208⁰С; ρ₁=1,16кг/м³; ρ₂=0,7кг/м³

Задача 10. Пылинки массой m = 10^-21 кг взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается на 1% ( ). Считать, что температура во всех слоях воздуха одинаковая и равна Т = 300 К.

Дано: m = 10-21 кг Т = 300 К	СИ 0,2 м
∆h -?

Решение:

Поскольку концентрация пылинок равномерно изменяется с высотой h, применим формулу Больцмана:

, (1)

где U – потенциальная энергия частиц, U = mgh; k – постоянная Больцмана,k =1,3810^-23 Дж/К.

В итоге получим:

. (2)

По условию задачи n << n ( 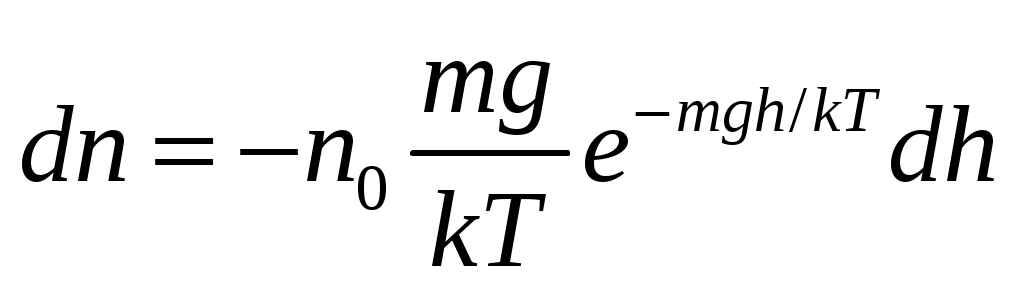), поэтому заменим изменение концентрации n на дифференциал dn. Продифференцируем (2) по h:

. (3)

Так как , то получим:

. (4)

Выразим из (4) искомую толщину слоя:

. (5)

Знак минус в (5) показывает, что с увеличением высоты (dh>0), концентрация молекул падает, поэтому n < 0.Опустим знак минус (в данной задаче он не существенен) и заменим дифференциалы конечными приращениями:

. (6)

Подставим в (6) числовые значения:



Ответ:

Задача 11. Кислород массой 320 г нагревают при постоянном давлении от 300 до 310 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.

Дано: m= 320 г T1 = 300 К T2 = 310 К	СИ 0,32 кг
Q -?ΔU -? A -?

Решение:

Количество теплоты, необходимое для нагревания газа при постоянном давлении, определим из первого начала термодинамики:

, (1)

где С_р– молярная изобарная теплоемкость, , где i = 5 для кислорода как двухатомного газа; – молярная масса газа, = 32 г/моль = .

Подставляя в (1) числовые значения, получим:



Изменение внутренней энергии газа:

. (2)

Подставляя числовые значения и учтя, что , получим:



Работа расширения газа при изобарном процессе:

, (3)

где .

Изменение объема газа при расширении можно найти из уравнения Клапейрона–Менделеева. Для двух состояний газа при изобарном процессе имеем:

(4)

(5)

и тогда вычитая почленно (5) из (4), получим:

(6)

Подставляя (6) в (3), находим:

= .

Ответ: Q = 2910Дж, ΔU = 2080Дж, A = 830 Дж.