МУ к ИДЗ по физике 1 семестр специальности ИС, ПГ (1). Учебнометодическое пособие для выполнения индивидуальных домашних заданий студентами очной формы обучения по направлениям подготовки Информационные системы и технологии

• Название: Учебнометодическое пособие для выполнения индивидуальных домашних заданий студентами очной формы обучения по направлениям подготовки Информационные системы и технологии
• Дата: 23.12.2021
• Размер: 1.12 Mb.
• Имя файла: МУ к ИДЗ по физике 1 семестр специальности ИС, ПГ (1).doc
• Тип: Учебно-методическое пособие; #315560
• страница: 4 из 6

Задача 12. Объем V₁= 7,5 л кислорода адиабатически сжимается до объема V₂= 1 л. В конце сжатия устанавливается давление р₂= 1,6 МПа. Под каким давлением находился газ до сжатия?

Дано: V1= 7,5 л V2= 1 л р2= 1,6 МПа	СИ 1,6∙106 Па
р1 - ?

Решение:

Согласно уравнению Пуассона рV^ = const, где –показатель адиабаты, для кислорода = 1,4.

Запишем уравнение Пуассона в виде:

.

Откуда Подставим числовые значения:

.

Ответ: р₁ = 95,29 кПа.
Задача 13. Как изменится энтропия (ΔS) 2 г водорода, занимающего объем 40 л при температуре 270 К, если давление увеличить вдвое при постоянной температуре, а затем повысить температуру до 320 К при постоянном объеме.

Дано: m= 2 г V = 40 л T1 = 270 К P2 = 2P1 T2 = 320 К V = const	СИ 2∙10-3 кг 40 м3
ΔS- ?

Решение:

Изменение энтропии определяется формулой:

, (1)

где dQ – количество теплоты, полученное в данном процессе.

Изменение энтропии согласно условию происходит за счет двух процессов: изотермического и изохорического. Тогда

. (2)

Количество теплоты dQ₁ и dQ₂найдем из первого начала термодинамики для этих процессов:

. (3)

Для изотермического процесса

. (4)

Давление рнайдем из уравнения Клапейрона–Менделеева , откуда

. (5)

Подставим (5) в (4):

(6)

(так как dT = 0 для T =const).

В результате, изменение энтропии S₁ составит:

, (7)

так как при T = const, р₁V₁ = р₂V₂.

Для изохорического процесса имеем:

, (8)

,

так как dV = 0и dA = 0при V = const.

. (9)

Подставив (9) и (6) в (2) получим:

. (10)

Подставляя численные значения, получим:



Ответ: S = –2,27 Дж/К.
Задача 14. Два одинаковых металлических шарика заряжены одноимен­но так, что величина заряда на одном шарике в 5 раз больше, чем на другом. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась сила взаимодействия между шарами?

Дано: r1=r2

Решение:

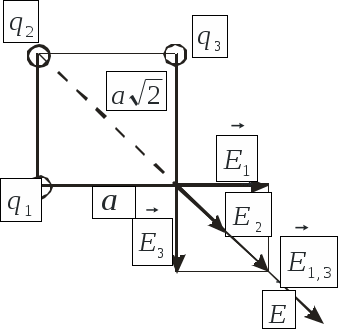
1.Будем считать, что оба шарика заряжены положительно. Для определения силы взаимодействия в обоих случаях воспользуемся законом Кулона: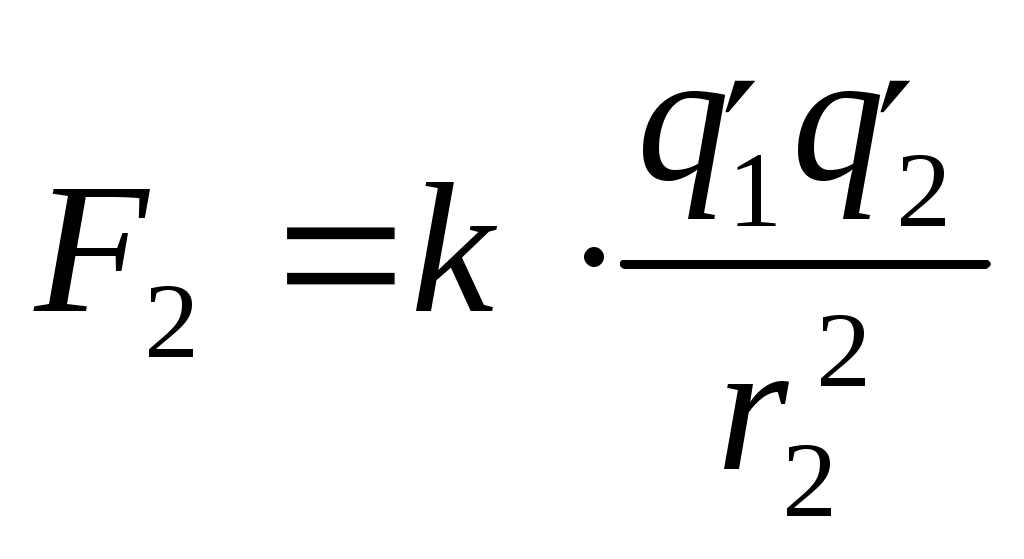

и (1),

где и - заряды шариков после того, как их привели в соприкосновение и раздвинули на прежнее расстояние.

2. Так как шарики одинаковые, то = .

3. По закону сохранения электрического заряда можно записать q₁+q₂= + или 5q₂+q₂=2 откуда

=3q₂ (2).

4. С учетом (1) и (2) найдем отношение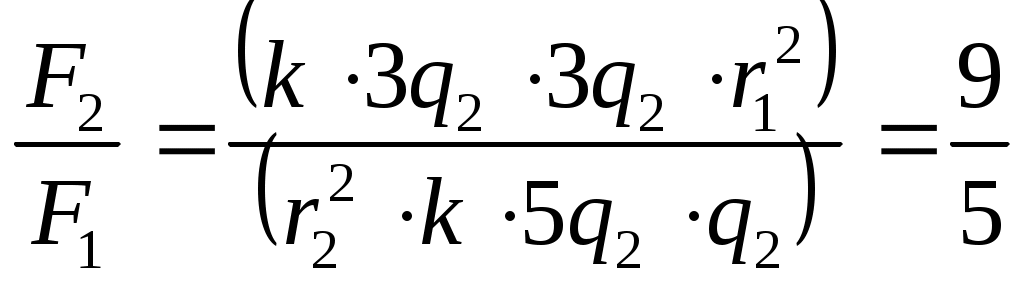

или .

Ответ: (сила взаимодействия увеличилась в 1,8 раза).

Задача 15. В трех вершинах квадрата со стороной 40 см находятся одинаковые положительные заряды величиной по 5^.10^-9 Кл каждый. Найти напряженность электрического поля, созданного системой зарядов, в четвертой вершине. Заряды находятся в диэлектрике с проницаемостью равной 2.

Дано: q1=q2=q3=5.10-9Кл a=40 см ε =2	СИ 0,4 м
E-?

Решение:

1.Воспользовавшись принципом суперпозиции для напряженности электрических полей, запишем выражение для напряженности поля в четвертой вершине (рис. 1.2)

, (1)

где –напряженности полей, создаваемых в четвертой вершине зарядами q₁, q₂, q₃.

2. Так как заряды точечные, то для модулей напряженностей имеем , . (3) 3.Модуль вектора для векторного сложения найдем по теореме Пифагора . (4)

Рис. 1.2

4.Так как векторы 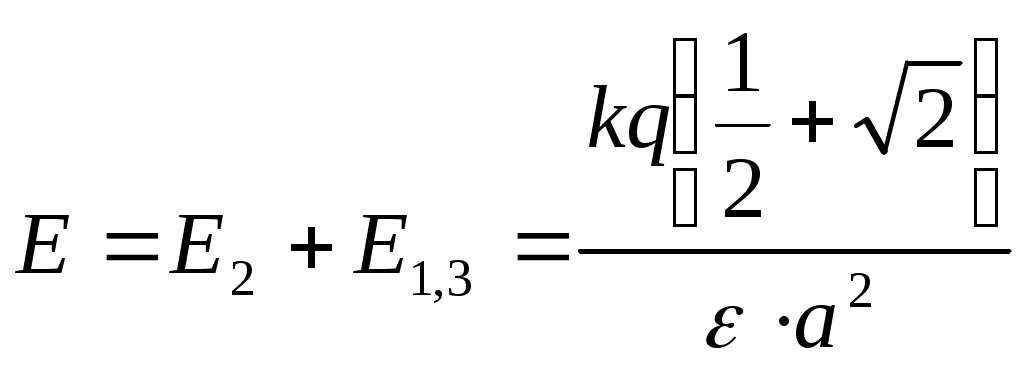и направлены по одной прямой, то модуль искомого вектора равен сумме модулей векторов и ,

то есть

(5).

Подставив в (5) численные значения в системе СИ и выполнив расчет, получим

В/м;

Ответ: Е=268,6 В/м.
Задача 16. Рассчитать напряженность поля, создаваемого равномерно заряженным цилиндром ( = 5 нКл/м) радиусом r =5см в точках, удаленных от оси цилиндра на расстояния R₁= 12см и R₂= 2 см. (рис.1.4).

Дано:  = 5 нКл/м R1= 12см R2= 2 см ε =1 r =5см	СИ 510-9 Кл/м 0,12 м 0,02 м 0,1 м 0,05 м
E1-? E2-?

Решение.



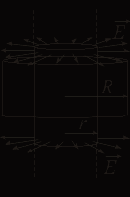Рис.1.4

1.Применим для решения данной задачи теорему Остроградского –Гаусса

₍₁₎

где Ф_Е- поток вектора напряженности электрического поля через некоторую замкнутую поверхность S; q- заряд тела.

2. В качестве замкнутой поверхностью простейшей формы, охватывающей все заряженное тело, выберем цилиндр радиуса R (R > r).Будем считать, что весь поток вектора напряженности идет через боковую поверхность охватывающего цилиндра.

3. Площадь боковой поверхности цилиндра радиуса Rрассчитывается по формуле

S = 2Rl. (2)

где l – длина цилиндра.

4.Тогда с учетом того, что равенство (1) можно переписать в виде

, (3)

где l – длина образующей охватывающей стержень цилиндрической поверхности.

5.Выразим из (3) напряженность, откуда имеем:

(R r). (4)

6. Подставим в (4)числовые значения:


7.При R r поле внутри цилиндра равно нулю, так как нет зарядов, охватываемых воображаемой поверхностью q= 0, Ф_Е = 0, следовательно Е₂ =0.

Ответ: Е₁ = 749,697В/м, Е₂ =0.

Задача 17. Электростатическое поле создано точечным зарядом q₀=10e в воде (ε = 80). При перемещении положительного заряда q из точки А, находящейся на расстоянии r₁=0,1 мм от заряда q₀, в точку В, находящуюся на расстоянии r₂ =0,2 мм от заряда q₀, силами электрического поля совершена работу 0,1 мкДж. Найти величину заряда q.

Дано: q0=10e e =1,610-19Кл r1=0,1 мм r2=0,2 мм А=0,1 мкДж	СИ 10-4 м 210-4 м 10-7 Дж
q-?

Решение:

1.Потенциал электрического поля, созданного точечным зарядом q₀ в воде:

(1)

2.Работа электрического поля по перемещению положительного заряда q из точки А в точку В равна:

A = -q ·Δφ (2)

. (3)

_{3.Выразим из полученного выражения q:}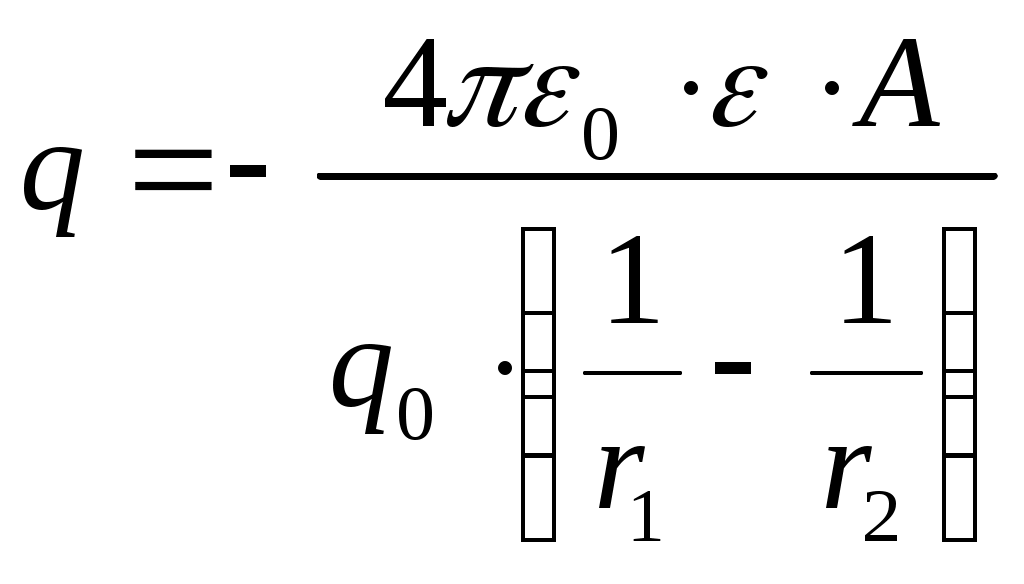

. (4)

4. Подставим в (4) числовые значения: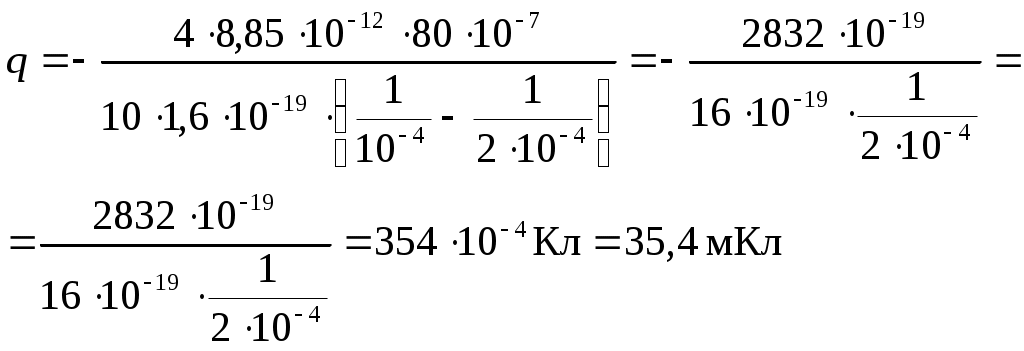



Ответ: q=35,4 мКл.
Задача 18. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость C такой батареи конденсаторов равна 89пФ. Площадь S каждой пластины равна 100 см². Диэлектрик - стекло. Какова толщина d стекла?

Дано: Cобщ=89 пФ S=100 см2 ε=7	СИ 89·10-12 Ф 10-2 м2
d-?

Решение:



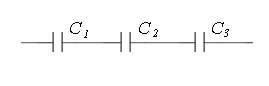Рис. 1.5

1.По условию задачи С₁=С₂=С₃=С.

2.Электроемкость батареи конденсаторов при их последовательном соединении (рис. 1.5):

; (1)

3.Электроемкость каждого плоского конденсаторы вычисляется по формуле:

. (2)

4.Тогда для батареи из трех конденсаторов:

. (3)

5. Выразим из (3) величину d:

(4)

6. Подставим в (4) числовые значения:



Ответ: d=2,3мм.